HDU 2242 考研路茫茫——空调教室（边双连通分量+树形dp+重边标号）

http://acm.hdu.edu.cn/showproblem.php?pid=2242

题意：

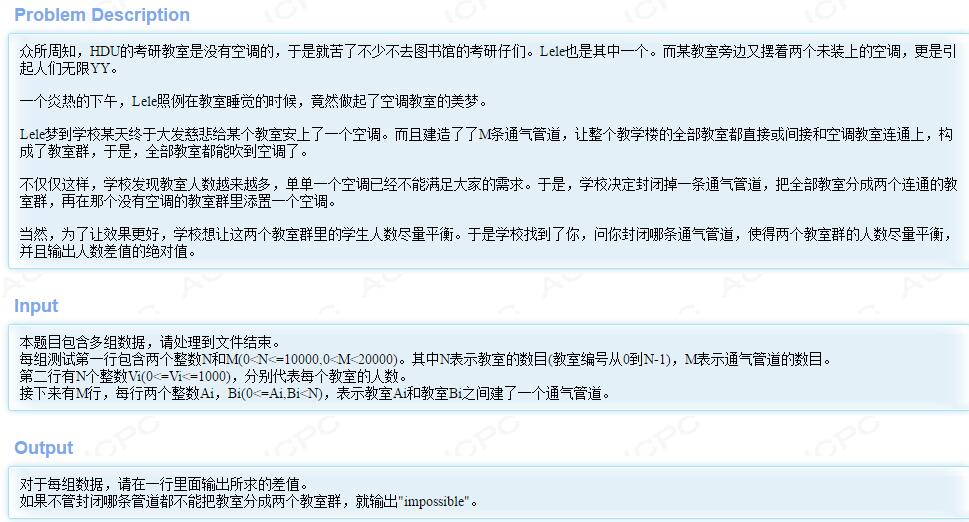
思路：
首先求一下双连通分量，如果只有一个双连通分量，那么无论断哪根管子，图还是连通的。

最后只需要根据双连通分量重新建图，在树上进行dp，分成两部分的最小差值。这个具体看代码就可以了。

需要注意的是，这道题目是存在重边的，在这个点上我WA了好久，那么怎么处理重边呢？

设置一个重边标记，跳过第一次父亲结点的反向边，但是第二次的话就必须处理，此时就是双连通的了。

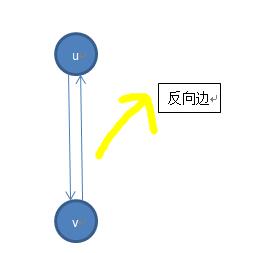
简单来说，如果图是没有重边的，那么我们在考虑反向边时，到父亲结点的反向边是不能考虑的，也就是else if(v!=fa)  lowu=min(lowu,pre[v])。

但是在这里是存在重边的，所以第一条父亲节点的反向边我们不能去考虑，但是之后就必须要去考虑，因为u，v之间如果有两条及以上的边，那它就是个双连通分量了，如果你用之前的（v!=fa）去判断，那肯定是错误的。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;

 int n, m;
 int tot;
 int cnt;
 int scc;
 int ans;
 int all_value;
 int val[maxn];
 int head[maxn];
 int head2[maxn];
 int dfs_clock;
 int pre[maxn];
 int low[maxn];
 int eccno[maxn];
 int sum[maxn];

 stack<int> S;

 struct node
 {
     int v;
     int next;
 }e[+];

 void addEdge(int u, int v)
 {
     e[tot].v=v;
     e[tot].next=head[u];
     head[u]=tot++;
 }

 void addEdge2(int u, int v)
 {
     e[tot].v=v;
     e[tot].next=head2[u];
     head2[u]=tot++;
 }

 void init()
 {
     tot=all_value=scc=dfs_clock=;
     memset(head,-,sizeof(head));
     memset(head2,-,sizeof(head2));
     memset(sum,,sizeof(sum));
     memset(pre,,sizeof(pre));
     memset(eccno,,sizeof(eccno));
 }

 int Tarjan(int u, int fa)
 {
     int flag=;   //标价重边
     int lowu=pre[u]=++dfs_clock;
     S.push(u);
     for(int i=head[u];i!=-;i=e[i].next)
     {
         int v=e[i].v;
         if(v==fa && !flag) {flag=;continue;}//考虑重边的情况，相当重要！
         if(!pre[v])
         {
             int lowv=Tarjan(v,u);
             lowu=min(lowu,lowv);
         }
         else lowu=min(lowu,pre[v]);
     }
     if(pre[u]==lowu)
     {
         scc++;
         for(;;)
         {
             int tmp=S.top(); S.pop();
             eccno[tmp]=scc;
             sum[scc]+=val[tmp];
             if(tmp==u)  break;
         }
     }
     return low[u]=lowu;
 }

 int dp(int u, int fa)
 {
     int ALL=sum[u];
     for(int i=head2[u];i!=-;i=e[i].next)
     {
         int v=e[i].v;
         if(v==fa)  continue;
         ALL+=dp(v,u);

     }
     ans=min(ans,abs(all_value-*ALL));
     return ALL;
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d",&n,&m))
     {
         init();
         for(int i=;i<n;i++)  {scanf("%d",&val[i]);all_value+=val[i];}
         while(m--)
         {
             int u, v;
             scanf("%d%d",&u,&v);
             addEdge(u,v);
             addEdge(v,u);
         }
         for(int i=;i<n;i++)
             if(!pre[i])  Tarjan(i,-);

         if(scc==)   {puts("impossible");continue;}
         for(int u=;u<n;u++)
         {
             for(int i=head[u];i!=-;i=e[i].next)
             {
                 int v=e[i].v;
                 if(eccno[u]!=eccno[v])  addEdge2(eccno[u],eccno[v]);
             }
         }
         ans=INF;
         dp(,-);
         printf("%d\n",ans);
     }
     return ;
 }