小波变换——哈尔小波，Haar

哈尔小波转换是于1909年由Alfréd Haar所提出，是小波变换（Wavelet transform）中最简单的一种变换，也是最早提出的小波变换。

Alfréd Haar，1885~1933，匈牙利数学家。哥廷根大学博士，导师是David Hilbert。Franz Joseph University教授。
Franz Joseph University是一所现在已经不存在的大学，有“小哥廷根”的称号，因为这里的数学系有大量的哥廷根大学毕业生执教。大学所在地Kolozsvár，在二战前后，一会儿归罗马尼亚，一会归匈牙利。当1945年，罗马尼亚最终接管该地之后，将学校的校舍分给了一所罗马尼亚大学，而将学校教师迁往别处，另建了一所大学。

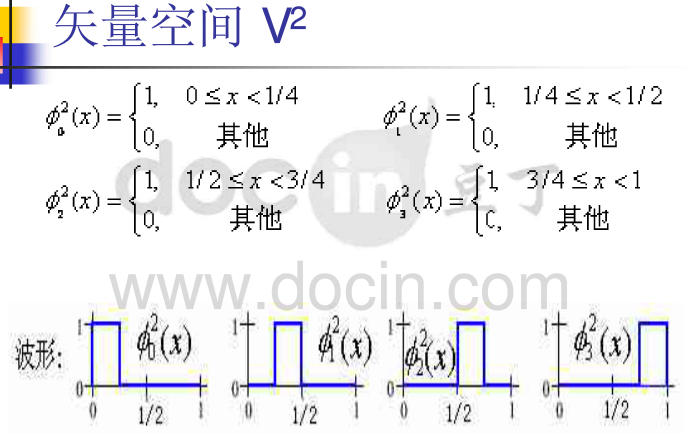
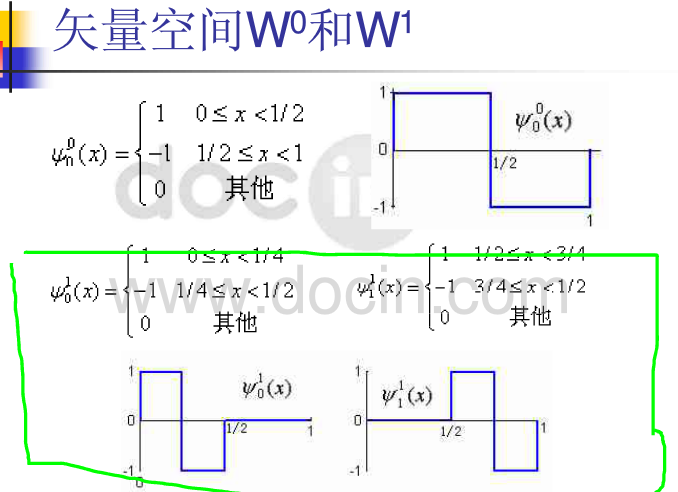
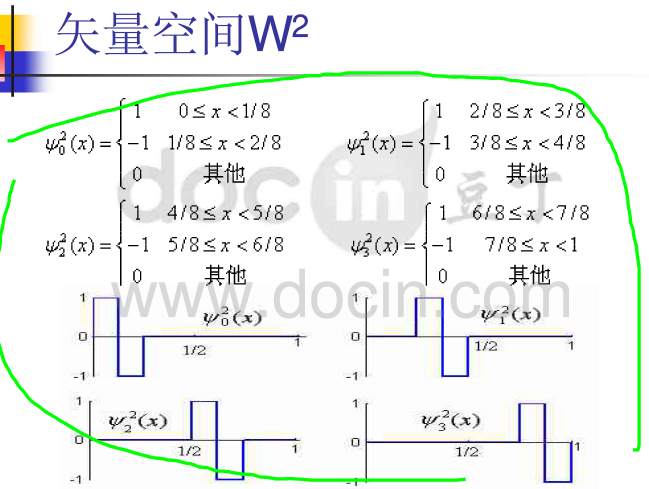
哈尔小波的母小波（mother wavelet）可表示为：

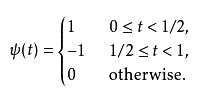
Haar Transform最早是由A. Haar在1910年“Zur theorie der orthogonalen funktionensysteme”中所提出，是一种最简单又可以反应出时变频谱（time-variant spectrum）的表示方法。

哈尔变换矩阵任取两行来进行内积的运算，所得到的内积皆为零。

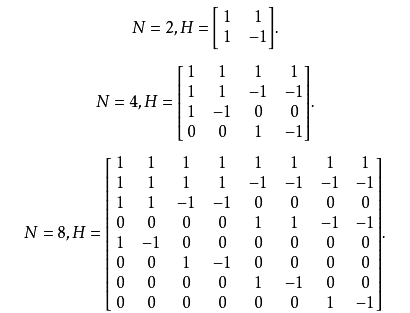
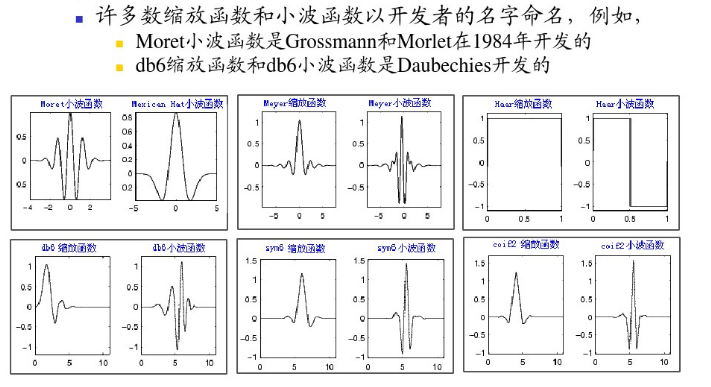
哈尔基函数(Haar basis function)。1909年提出。

---

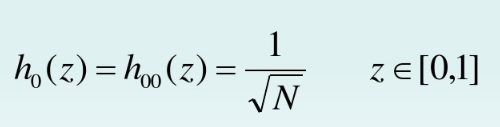
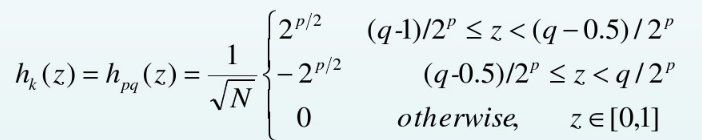
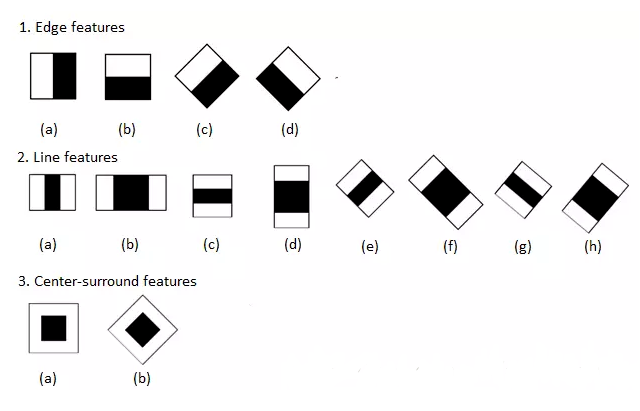
【转载自】

[图文]第7章 - 小波变换和多分辨率处理 - 百度文库 https://wenku.baidu.com/view/41ddf4eab52acfc788ebc900.html

HAAR小波变换 - 豆丁网 https://www.docin.com/p-663309428.html

哈尔小波转换_百度百科 https://baike.baidu.com/item/%E5%93%88%E5%B0%94%E5%B0%8F%E6%B3%A2%E8%BD%AC%E6%8D%A2/22781894?fr=aladdin

图像处理理论（四）——HOG, Haar, ISP - antkillerfarm的专栏 - CSDN博客 https://blog.csdn.net/antkillerfarm/article/details/79694086