MT【53】对数平均做数列放缩
【从最简单的做起】——波利亚
请看下面三道循序渐进不断加细的题。
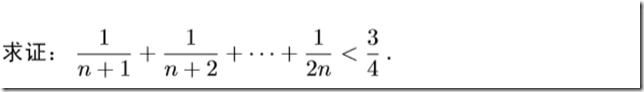
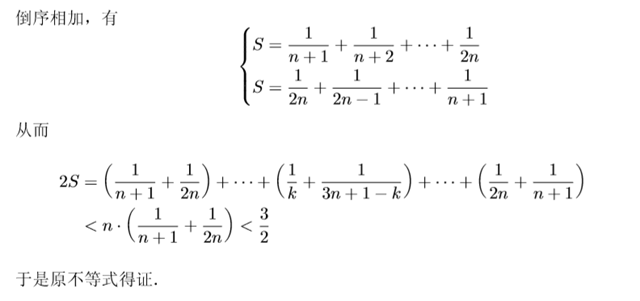
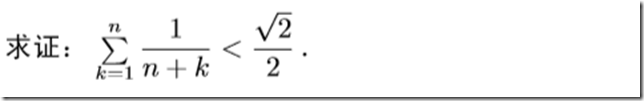
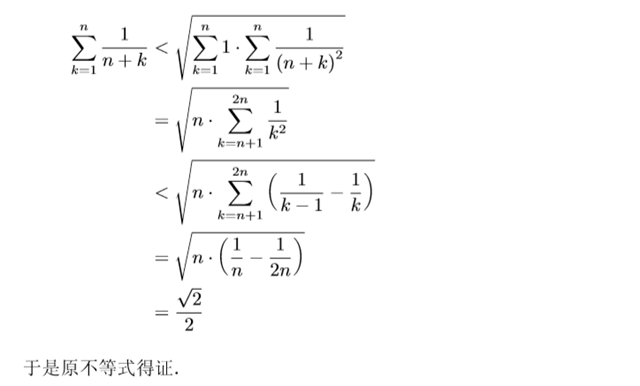
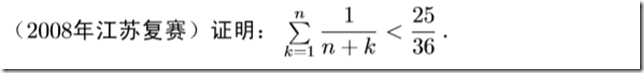
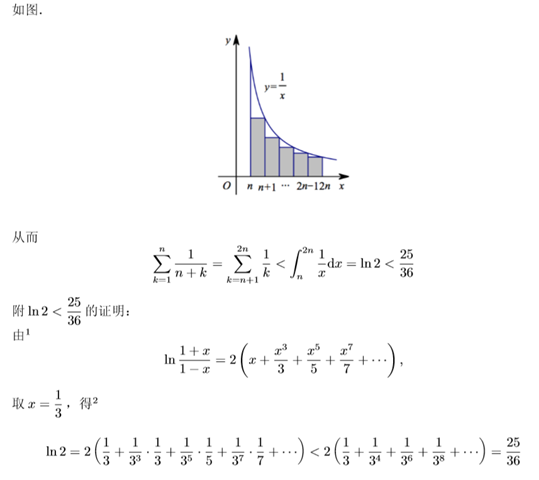
评:随着右边的不断加细,解决问题的方法也越来越“高端”.当然最佳值$ln2$我们可以用相对
容易的方法来证明:
$\because ln(2k+1)-ln(2k-1)>\frac{1}{k}$两边$k$从$n+1$取到$2n$得$$ln2>\sum_{k=1}^{n}{\frac{1}{n+k}}$$
MT【53】对数平均做数列放缩的更多相关文章
- MT【26】ln(1+x)的对数平均放缩
评:1.某种程度上$ln(1+x)\ge \frac{2x}{2+x}$是最佳放缩. 2.这里涉及到分母为幂函数型的放缩技巧,但是不够强,做不了这题.
- MT【148】凸数列
(2018浙江省赛13题) 设实数$x_1,x_2,\cdots,x_{2018}$满足$x_{n+1}^2\le x_nx_{n+2},(n=1,2,\cdots,2016)$和$\prod\lim ...
- MT【307】周期数列
(2017浙江省数学竞赛) 设数列$\{a_n\}$满足:$|a_{n+1}-2a_n|=2,|a_n|\le2,n\in N^+$证明:如果$a_1$为有理数,则从某项后$\{a_n\}$为周期数列 ...
- hdu5988(费用流,对数相乘做加法)
题意:一个网络流的图,有n个点,从1~n,然后m条边,每个点有两个值,一个是人的数量si一个是饭的数量bi.每条m边有容量ci,还有走上去可能踩断电线的概率pi(第一次踩上去没有事,之后都要p概率). ...
- MT【256】2016四川高考解答压轴题
(2016四川高考数学解答压轴题)设函数$f(x)=ax^2-a-\ln x,a\in R$. 1)讨论$f(x)$的单调性;2)确定$a$的所有可能值,使得$f(x)>\dfrac{1}{x} ...
- [PHP] 2018年终总结
去掉敏感信息后的不完整版 ==========================================================================2018年12月29日 记 ...
- 论文阅读笔记三十:One pixel attack for fooling deep neural networks(CVPR2017)
论文源址:https://arxiv.org/abs/1710.08864 tensorflow代码: https://github.com/Hyperparticle/one-pixel-attac ...
- [代码解析]Mask R-CNN介绍与实现(转)
文章来源 DFann 版权声明:如果你觉得写的还可以,可以考虑打赏一下.转载请联系. https://blog.csdn.net/u011974639/article/details/78483779 ...
- InnoDB引擎中的索引与算法9
5.1 InnoDB支持以下几种常见的索引: B+树索引 全文索引 哈希索引(自适应哈希索引) 关于哈希索引的说明: -- 1.InnoDB的哈希索引是自适应的,其根据表的使用情况自动生成哈希索引,不 ...
随机推荐
- SQL Server中使用convert进行日期转换(转载)
一般存入数据库中的时间格式为yyyy-mm-dd hh:mm:ss 如果要转换为yyyy-mm-dd 短日期格式.可以使用convert函数.下面是sqlserver帮助中关于convert函数的声 ...
- React-引入图片的方法
方法一: import imgURL from '../../images/logo.png'; <img src={imgURL} alt="1"/> 方法二: &l ...
- Quartz_配置
quartz_jobs.xml job 任务 其实就是1.x版本中的<job-detail>,这个节点是用来定义每个具体的任务的,多个任务请创建多个job节点即可 name(必填) 任务名 ...
- 在Mac终端显示 Git 当前所在分支
1.进入你的home目录 cd ~ 2.编辑.bashrc文件 vi .bashrc 3.将下面的代码加入到文件的最后处 function git_branch { branch="`git ...
- 使用rem进行自适应页面布局
设计师给到我们前端的设计稿一般是按照iphone6屏幕(iphone6 两倍屏 设备 分辨率(物理尺寸) 屏幕宽高 PPI 状态栏高度 导航栏高度 标签栏高度 iPhone6 750×1334 px ...
- Python_初识函数和返回值_22
#len s = '金老板小护士' len(s) def my_len(): #自定义函数 i = 0 for k in s: i += 1 print(i) length = my_len() pr ...
- 后台跑包方法 断开ssh程序也能继续执行的方法screen命令
aircrack-ng -w 字典路径 握手包路径 screen -S 001创建会话 screen -ls 列出窗口列表 screen -r 5位数字 进入会话指令 如果会话恢复不了,则是有可能 ...
- c#词频统计命令行程序
这里将用c#写一个关于词频统计的命令行程序. 预计时间分配:输入处理3h.词条排序打印2h.测试3h. 实际时间分配:输入处理1h.词条排序打印2h.测试3h.程序改进优化6h. 下面将讲解程序的完成 ...
- 软件工程导论课后习题Github作业(把一个英文句子中的单词次序逆序,单词中字母正常排列)
Java源代码 package yly; import java.util.Scanner; public class ruanjian { public static void main(St ...
- Spring整合SpringMVC
整合:把在springMVC配置文件中的spring提取出来整合为另一份配置文件 希望: 1).Spring的配置文件只是用来配置和业务逻辑有关的功能(数据源.事务控制.切面....) 2).Spri ...
