51nod1238 最小公倍数之和 V3

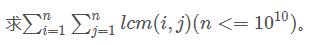
又被这神仙题给坑爆了。

神仙题解。

一开始我把lcm变成ij/gcd然后按照常规套路去推，推到最后发现不是miu * Id而是miu · Id......这还搞鬼啊。

正解居然跟这个差不多，先转成求其中一部分的函数，然后再加和......这谁顶得住呀。

大概就是先求这个

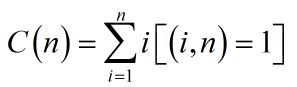
一顿操作之后得到了phi有关的式子......

然后原式就是这个

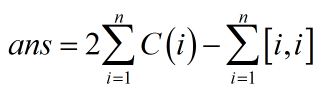
然后带进去推一推就出来杜教筛了...这第一步真是神奇。

最后是这个。

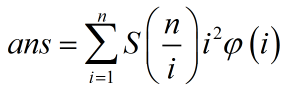
按照套路，前面分块，后面配一个g(x) = x²即可。

 #include <cstdio>
 #include <map>

 typedef long long LL;
 const int N = , T = ;
 const LL MO = ;

 std::map<LL, LL> mp;
 LL inv2, inv6, F[N];
 int p[N], top, phi[N];
 bool vis[N];

 inline LL qpow(LL a, LL b) {
     LL ans = ;
     while(b) {
         if(b & ) ans = ans * a % MO;
         a = a * a % MO;
         b = b >> ;
     }
     return ans;
 }

 inline LL S(LL x) {
     x %= MO;
     return x * (x + ) /  % MO;
 }

 inline LL G(LL x) {
     x %= MO;
     return (x <<  | ) % MO * (x + ) % MO * x % MO * inv6 % MO;
 }

 inline LL H(LL x) {
     LL temp = S(x);
     return temp * temp % MO;
 }

 inline void getp(int n) {
     phi[] = ;
     for(int i = ; i <= n; i++) {
         if(!vis[i]) {
             p[++top] = i;
             phi[i] = i - ;
         }
         for(int j = ; j <= top && i * p[j] <= n; j++) {
             vis[i * p[j]] = ;
             if(i % p[j] == ) {
                 phi[i * p[j]] = phi[i] * p[j];
                 break;
             }
             phi[i * p[j]] = phi[i] * (p[j] - );
         }
     }
     for(int i = ; i <= n; i++) {
         F[i] = (F[i - ] + 1ll * i * i % MO * phi[i] % MO) % MO;
     }
     return;
 }

 LL getF(LL x) {
     if(x <= ) return ;
     if(x <= T) return F[x];
     if(mp.count(x)) return mp[x];
     LL ans = H(x);
     for(LL i = , j; i <= x; i = j + ) {
         j = x / (x / i);
         ans -= (G(j) - G(i - ) + MO) * getF(x / i) % MO;
         ans %= MO;
     }
     return mp[x] = (ans + MO) % MO;
 }

 int main() {
     inv2 = (MO + ) / ;
     inv6 = qpow(, MO - );
     getp(T);
     LL ans = , n;
     scanf("%lld", &n);
     for(LL i = , j; i <= n; i = j + ) {
         j = n / (n / i);
         ans += S(n / i) * (getF(j) - getF(i - ) + MO) % MO;
         ans %= MO;
     }
     printf("%lld\n", (ans + MO) % MO);
     return ;
 }

AC代码