HMM模型学习笔记（维特比算法）

维特比算法（Viterbi）

维特比算法

 编辑

维特比算法是一种动态规划算法用于寻找最有可能产生观测事件序列的-维特比路径-隐含状态序列,特别是在马尔可夫信息源上下文和隐马尔可夫模型中。术语“维特比路径”和“维特比算法”也被用于寻找观察结果最有可能解释相关的动态规划算法。例如在统计句法分析中动态规划算法可以被用于发现最可能的上下文无关的派生(解析)的字符串，有时被称为“维特比分析”。

 

中文名

维特比算法

外文名

Viterbi Algorithm

提出时间

1967年

提出者

安德鲁·维特比

应用领域

CDMA和GSM数字蜂窝网络等

维特比算法由安德鲁·维特比(Andrew Viterbi)于1967年提出，用于在数字通信链路中解卷积以消除噪音。 此算法被广泛应用于CDMA和GSM数字蜂窝网络、拨号调制解调器、卫星、深空通信和802.11无线网络中解卷积码。现今也被常常用于语音识别、关键字识别、计算语言学和生物信息学中。例如在语音(语音识别)中，声音信号作为观察到的事件序列,而文本字符串,被看作是隐含的产生声音信号的原因，因此可对声音信号应用维特比算法寻找最有可能的文本字符串。[1] 

数学之美维特比算法

维特比算法的基础可以概括成下面三点：

1. 如果概率最大的路径p(或者说最短路径)经过某个点，比如途中的X22，那么这条路径上的起始点S到X22的这段子路径Q，一定是S到X22之间的最短路径。否则，用S到X22的最短路径R替代Q，便构成一条比P更短的路径，这显然是矛盾的。证明了满足最优性原理。
2. 从S到E的路径必定经过第i个时刻的某个状态，假定第i个时刻有k个状态，那么如果记录了从S到第i个状态的所有k个节点的最短路径，最终的最短路径必经过其中一条，这样，在任意时刻，只要考虑非常有限的最短路即可。

3. 结合以上两点，假定当我们从状态i进入状态i+1时，从S到状态i上各个节的最短路径已经找到，并且记录在这些节点上，那么在计算从起点S到第i+1状态的某个节点Xi+1的最短路径时，只要考虑从S到前一个状态i所有的k个节点的最短路径，以及从这个节点到Xi+1，j的距离即可。

 

 

应用：

推断天气等

尝试用高中概率知识去理解一下 Veterbi 算法。内容绝对粗浅，100% 抄袭，欢迎指正。用一个别人家的栗子来说一下。

1.题目背景：

从前有个村儿，村里的人的身体情况只有两种可能：健康或者发烧。
假设这个村儿的人没有体温计或者百度这种神奇东西，他唯一判断他身体情况的途径就是到村头我的偶像金正月的小诊所询问。
月儿通过询问村民的感觉，判断她的病情，再假设村民只会回答正常、头晕或冷。
有一天村里奥巴驴就去月儿那去询问了。
第一天她告诉月儿她感觉正常。
第二天她告诉月儿感觉有点冷。
第三天她告诉月儿感觉有点头晕。
那么问题来了，月儿如何根据阿驴的描述的情况，推断出这三天中阿驴的一个身体状态呢?
为此月儿上百度搜 google ，一番狂搜，发现维特比算法正好能解决这个问题。月儿乐了。

2.已知情况：

隐含的身体状态 = { 健康 , 发烧 }

可观察的感觉状态 = { 正常 , 冷 , 头晕 }

月儿预判的阿驴身体状态的概率分布 = { 健康：0.6 , 发烧： 0.4 }

月儿认为的阿驴身体健康状态的转换概率分布 = {
健康->健康： 0.7 ,
健康->发烧： 0.3 ,
发烧->健康：0.4 ,
发烧->发烧： 0.6
}

月儿认为的在相应健康状况条件下，阿驴的感觉的概率分布 = {
健康，正常：0.5 ，冷 ：0.4 ，头晕： 0.1 ；
发烧，正常：0.1 ，冷 ：0.3 ，头晕： 0.6 
}
阿驴连续三天的身体感觉依次是： 正常、冷、头晕 。

3.题目：

已知如上，求：阿驴这三天的身体健康状态变化的过程是怎么样的？

4.过程：

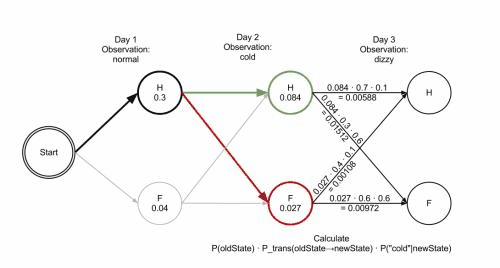
根据 Viterbi 理论，后一天的状态会依赖前一天的状态和当前的可观察的状态。那么只要根据第一天的正常状态依次推算找出到达第三天头晕状态的最大的概率，就可以知道这三天的身体变化情况。
传不了图片，悲剧了。。。
1.初始情况：

• P(健康) = 0.6，P(发烧)=0.4。

2.求第一天的身体情况：
计算在阿驴感觉正常的情况下最可能的身体状态。

• P(今天健康) = P(正常|健康)*P(健康|初始情况) = 0.5 * 0.6 = 0.3
• P(今天发烧) = P(正常|发烧)*P(发烧|初始情况) = 0.1 * 0.4 = 0.04

那么就可以认为第一天最可能的身体状态是：健康。
3.求第二天的身体状况：
计算在阿驴感觉冷的情况下最可能的身体状态。
那么第二天有四种情况，由于第一天的发烧或者健康转换到第二天的发烧或者健康。

• P(前一天发烧，今天发烧) = P(前一天发烧)*P(发烧->发烧)*P(冷|发烧) = 0.04 * 0.6 * 0.3 = 0.0072
• P(前一天发烧，今天健康) = P(前一天发烧)*P(发烧->健康)*P(冷|健康) = 0.04 * 0.4 * 0.4 = 0.0064
• P(前一天健康，今天健康) = P(前一天健康)*P(健康->健康)*P(冷|健康) = 0.3 * 0.7 * 0.4 = 0.084
• P(前一天健康，今天发烧) = P(前一天健康)*P(健康->发烧)*P(冷|发烧) = 0.3 * 0.3 *.03 = 0.027

那么可以认为，第二天最可能的状态是：健康。
4.求第三天的身体状态：
计算在阿驴感觉头晕的情况下最可能的身体状态。

• P(前一天发烧，今天发烧) = P(前一天发烧)*P(发烧->发烧)*P(头晕|发烧) = 0.027 * 0.6 * 0.6 = 0.00972
• P(前一天发烧，今天健康) = P(前一天发烧)*P(发烧->健康)*P(头晕|健康) = 0.027 * 0.4 * 0.1 = 0.00108
• P(前一天健康，今天健康) = P(前一天健康)*P(健康->健康)*P(头晕|健康) = 0.084 * 0.7 * 0.1 = 0.00588
• P(前一天健康，今天发烧) = P(前一天健康)*P(健康->发烧)*P(头晕|发烧) = 0.084 * 0.3 *0.6 = 0.01512

那么可以认为：第三天最可能的状态是发烧。

5.结论

根据如上计算。这样月儿断定，阿驴这三天身体变化的序列是：健康->健康->发烧。

这个算法大概就是通过已知的可以观察到的序列，和一些已知的状态转换之间的概率情况，通过综合状态之间的转移概率和前一个状态的情况计算出概率最大的状态转换路径，从而推断出隐含状态的序列的情况。

转载自：https://www.cnblogs.com/Renyi-Fan/p/7865985.html

参考：https://zh.wikipedia.org/wiki/%E7%BB%B4%E7%89%B9%E6%AF%94%E7%AE%97%E6%B3%95