Kosaraju 算法检测有向图的强连通性

给定一个有向图 G = (V, E) ，对于任意一对顶点 u 和 v，有 u --> v 和 v --> u，亦即，顶点 u 和 v 是互相可达的，则说明该图 G 是强连通的（Strongly Connected）。如下图中，任意两个顶点都是互相可达的。

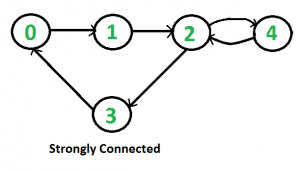
对于无向图，判断图是否是强连通的，可以直接使用深度优先搜索（DFS）或广度优先搜索（BFS），从任意一个顶点出发，如果遍历的结果包含所有的顶点，则说明图是强连通的。

而对于有向图，则不能使用 DFS 或 BFS 进行直接遍历来判断。如下图中，如果从顶点 0 开始遍历则可判断是强连通的，而如果从其它顶点开始遍历则无法抵达所有节点。

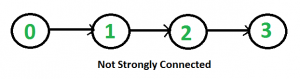
那么，该如何判断有向图的强连通性呢？

实际上，解决该问题的较好的方式就是使用强连通分支算法（SCC：Strongly Connected Components），可以在 O(V+E) 时间内找到所有的 SCC。如果 SCC 的数量是 1，则说明整个图是强连通的。

有向图 G = (V, E) 的一个强连通分支是一个最大的顶点集合 C，C 是 V 的子集，对于 C 中的每一对顶点 u 和 v，有 u --> v 和 v --> u，亦即，顶点 u 和 v 是互相可达的。

实现 SCC 的一种算法就是 Kosaraju 算法。Kosaraju 算法基于深度优先搜索（DFS），并对图进行两次 DFS 遍历，算法步骤如下：

1. 初始化设置所有的顶点为未访问的；
2. 从任意顶点 v 开始进行 DFS 遍历，如果遍历结果没有访问到所有顶点，则说明图不是强连通的；
3. 置换整个图（Reverse Graph）；
4. 设置置换后的图中的所有顶点为未访问过的；
5. 从与步骤 2 中相同的顶点 v 开始做 DFS 遍历，如果遍历没有访问到所有顶点，则说明图不是强连通的，否则说明图是强连通的。

Kosaraju 算法的思想就是，如果从顶点 v 可以抵达所有顶点，并且所有顶点都可以抵达 v，则说明图是强连通的。

 using System;
 using System.Collections.Generic;
 using System.Linq;

 namespace GraphAlgorithmTesting
 {
   class Program
   {
     static void Main(string[] args)
     {
       Graph g = new Graph();
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );

       Console.WriteLine();
       Console.WriteLine("Graph Vertex Count : {0}", g.VertexCount);
       Console.WriteLine("Graph Edge Count : {0}", g.EdgeCount);
       Console.WriteLine();

       Console.WriteLine("Is graph strongly connected: {0}", g.Kosaraju());

       Console.ReadKey();
     }

     class Edge
     {
       public Edge(int begin, int end, int weight)
       {
         this.Begin = begin;
         this.End = end;
         this.Weight = weight;
       }

       public int Begin { get; private set; }
       public int End { get; private set; }
       public int Weight { get; private set; }

       public override string ToString()
       {
         return string.Format(
           "Begin[{0}], End[{1}], Weight[{2}]",
           Begin, End, Weight);
       }
     }

     class Graph
     {
       private Dictionary<int, List<Edge>> _adjacentEdges
         = new Dictionary<int, List<Edge>>();

       public Graph(int vertexCount)
       {
         this.VertexCount = vertexCount;
       }

       public int VertexCount { get; private set; }

       public IEnumerable<int> Vertices { get { return _adjacentEdges.Keys; } }

       public IEnumerable<Edge> Edges
       {
         get { return _adjacentEdges.Values.SelectMany(e => e); }
       }

       public int EdgeCount { get { return this.Edges.Count(); } }

       public void AddEdge(int begin, int end, int weight)
       {
         if (!_adjacentEdges.ContainsKey(begin))
         {
           var edges = new List<Edge>();
           _adjacentEdges.Add(begin, edges);
         }

         _adjacentEdges[begin].Add(new Edge(begin, end, weight));
       }

       public bool Kosaraju()
       {
         // Step 1: Mark all the vertices as not visited (For first DFS)
         bool[] visited = new bool[VertexCount];
         for (int i = ; i < visited.Length; i++)
           visited[i] = false;

         // Step 2: Do DFS traversal starting from first vertex.
         DFS(, visited);

         // If DFS traversal doesn’t visit all vertices, then return false.
         for (int i = ; i < VertexCount; i++)
           if (visited[i] == false)
             return false;

         // Step 3: Create a reversed graph
         Graph reversedGraph = Transpose();

         // Step 4: Mark all the vertices as not visited (For second DFS)
         for (int i = ; i < visited.Length; i++)
           visited[i] = false;

         // Step 5: Do DFS for reversed graph starting from first vertex.
         // Staring Vertex must be same starting point of first DFS
         reversedGraph.DFS(, visited);

         // If all vertices are not visited in second DFS, then
         // return false
         for (int i = ; i < VertexCount; i++)
           if (visited[i] == false)
             return false;

         return true;
       }

       void DFS(int v, bool[] visited)
       {
         visited[v] = true;

         if (_adjacentEdges.ContainsKey(v))
         {
           foreach (var edge in _adjacentEdges[v])
           {
             if (!visited[edge.End])
               DFS(edge.End, visited);
           }
         }
       }

       Graph Transpose()
       {
         Graph g = new Graph(this.VertexCount);

         foreach (var edge in this.Edges)
         {
           g.AddEdge(edge.End, edge.Begin, edge.Weight);
         }

         return g;
       }
     }
   }
 }

参考资料

• Connectivity in a directed graph
• Strongly Connected Components
• Tarjan's Algorithm to find Strongly Connected Components

本篇文章《Kosaraju 算法检测有向图的强连通性》由 Dennis Gao 发表自博客园，未经作者本人同意禁止任何形式的转载，任何自动或人为的爬虫转载行为均为耍流氓。