剑指Offer面试题:9.二进制中1的个数
一、题目:二进制中1的个数
题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。
二、可能引起死循环的解法
一个基本的思路:先判断整数二进制表示中最右边一位是不是1。接着把输入的整数右移一位,此时原来处于从右边数起的第二位被移到最右边了,再判断是不是1。这样每次移动一位,直到整个整数变成0为止。
怎么判断一个整数的最右边是不是1:只要把整数和1做位与运算看结果是不是0就知道了。
public static int NumberOf1Solution1(int n)
{
int count = ; while (n > )
{
if ((n & ) == )
{
count++;
} n = n >> ;
} return count;
}
PS:右移运算符m>>n表示把m右移n位。右移n位的时候,最右边的n位将被丢弃。如果数字原先是一个正数,则右移之后在最左边补n个0;如果数字原先是负数,则右移之后在最左边补n个1。例如下面对两个八位二进制数进行右移操作:
00001010>>2=00000010
10001010>>3=11110001
那么,问题来了:上面的方法如果输入一个负数,比如0x80000000,如果一直做右移运算,最终这个数字就会变成0xFFFFFFFF而陷入死循环。
三、避免引起死循环的解法
为了避免死循环,我们可以不右移输入的数字i:
(1)首先把i和1做与运算,判断i的最低位是不是为1。
(2)接着把1左移一位得到2,再和i做与运算,就能判断i的次低位是不是1。
(3)这样反复左移,每次都能判断i的其中一位是不是1。
public static int NumberOf1Solution2(int n)
{
int count = ;
uint flag = ;
while (flag >= )
{
if ((n & flag) > )
{
count++;
} flag = flag << ;
} return count;
}
PS:这个解法中循环的次数等于整数二进制的位数,32位的整数需要循环32次。
四、高效新颖的解法
把一个整数减去1,再和原整数做与运算,会把该整数最右边一个1变成0。那么一个整数的二进制表示中有多少个1,就可以进行多少次这样的操作。

public static int NumberOf1Solution3(int n)
{
int count = ; while (n > )
{
count++;
n = (n - ) & n;
} return count;
}
PS:把一个整数减去1之后再和原来的整数做位与运算,得到的结果相当于是把整数的二进制表示中的最右边一个1变成0。很多二进制的问题都可以用这个思路解决。
五、单元测试
5.1 测试用例
// 输入0,期待的输出是0
[TestMethod]
public void NumberOfOneInBinaryTest1()
{
Assert.AreEqual(BinaryHelper.NumberOf1Solution2(),);
Assert.AreEqual(BinaryHelper.NumberOf1Solution3(),);
} // 输入1,期待的输出是1
[TestMethod]
public void NumberOfOneInBinaryTest2()
{
Assert.AreEqual(BinaryHelper.NumberOf1Solution2(), );
Assert.AreEqual(BinaryHelper.NumberOf1Solution3(), );
} // 输入10,期待的输出是2
[TestMethod]
public void NumberOfOneInBinaryTest3()
{
Assert.AreEqual(BinaryHelper.NumberOf1Solution2(), );
Assert.AreEqual(BinaryHelper.NumberOf1Solution3(), );
} // 输入0x7FFFFFFF,期待的输出是31
[TestMethod]
public void NumberOfOneInBinaryTest4()
{
Assert.AreEqual(BinaryHelper.NumberOf1Solution2(0x7FFFFFFF), );
Assert.AreEqual(BinaryHelper.NumberOf1Solution3(0x7FFFFFFF), );
} // 输入0xFFFFFFFF(负数),期待的输出是32
[TestMethod]
public void NumberOfOneInBinaryTest5()
{
Assert.AreEqual(BinaryHelper.NumberOf1Solution2(0xFFFFFFFF), );
Assert.AreEqual(BinaryHelper.NumberOf1Solution3(0xFFFFFFFF), );
} // 输入0x80000000(负数),期待的输出是0
[TestMethod]
public void NumberOfOneInBinaryTest6()
{
Assert.AreEqual(BinaryHelper.NumberOf1Solution2(0x80000000), );
Assert.AreEqual(BinaryHelper.NumberOf1Solution3(0x80000000), );
}
5.2 测试结果
(1)测试通过情况:
(2)代码覆盖率:
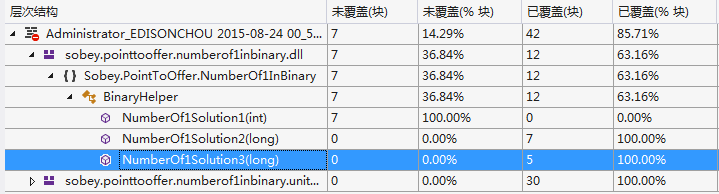
剑指Offer面试题:9.二进制中1的个数的更多相关文章
- 剑指Offer - 九度1513 - 二进制中1的个数
剑指Offer - 九度1513 - 二进制中1的个数2013-11-29 23:35 题目描述: 输入一个整数,输出该数二进制表示中1的个数.其中负数用补码表示. 输入: 输入可能包含多个测试样例. ...
- 【剑指Offer】11、二进制中1的个数
题目描述: 输入一个整数,输出该数二进制表示中1的个数.其中负数用补码表示. 解题思路: 本题有以下两个解决方案: (1)依次判断每一位.判断的方法是先与1相与,为1则说明该位为1 ...
- 剑指offer 11. 位运算 二进制中1的个数
题目描述 输入一个整数,输出该数二进制表示中1的个数.其中负数用补码表示. //思想:用1(1自身左移运算,其实后来就不是1了)和n的每位进行位与,来判断1的个数 private stat ...
- 剑指offer(11)二进制中1的个数
题目描述 输入一个整数,输出该数二进制表示中1的个数.其中负数用补码表示. 题目分析 首先我们要了解计算机中负数使用补码表示的,原码.补码的概念以及原理可以参考这里,这个题目我们应该从二进制入手,值得 ...
- 剑指offer【12】- 二进制中1的个数
输入一个整数,输出该数二进制表示中1的个数.其中负数用补码表示. public class Solution { public int NumberOf1(int n) { String str = ...
- 剑指offer编程题Java实现——面试题10二进制中1的个数
题目: 请实现一个函数,输入一个整数,输出该整数二进制表示中1的个数.例如,把9表示成二进制是1001,有2位是1,该函数输出2解法:把整数减一和原来的数做与运算,会把该整数二进制表示中的最低位的1变 ...
- 剑指offer面试题3 二维数组中的查找(c)
剑指offer面试题三:
- 剑指offer——面试题15:二进制中 1的个数
// 面试题15:二进制中1的个数 // 题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数.例如 // 把9表示成二进制是1001,有2位是1.因此如果输入9,该函数输出2. #inc ...
- 剑指offer面试题3二维数组中的查找
题目: 在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序.请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数. 需要与面试官确认的是,这 ...
- 剑指offer-面试题10:二进制中1的个数
题目:请实现一个函数,输入一个函数,输出该数二进制表示中1的个数.例如把9 表示成二进制是1001,有2位是1.因此如果输入9,该函数输出2. 这道题最典型的方法就是用移位统计,就比如统计9的二进制1 ...
随机推荐
- JS 数据类型转换
JS 数据类型转换 方法主要有三种 转换函数.强制类型转换.利用js变量弱类型转换. 1. 转换函数: js提供了parseInt()和parseFloat()两个转换函数.前者把值转换成整数,后者把 ...
- C++ 系列:C++ 对象模型
1 何为C++对象模型 C++对象模型可以概括为以下2部分: 1.语言中直接支持面向对象程序设计的部分: 2.对于各种支持的底层实现机制 语言中直接支持面向对象程序设计的部分,如构造函数.析 ...
- [PHP]加密解密函数
非常给力的authcode加密函数,Discuz!经典代码(带详解) function authcode($string, $operation = 'DECODE', $key = '', $exp ...
- ng1.3+表单验证<AngularJs>
前一篇文章说过,ng1.3+以后对于表单验证有了优化,它不再需要一个详细的表达式状态创建元素显示或隐藏. 例如:我们在ng1.3之前的版本都需要如下写法: <div class="er ...
- “玲珑杯”ACM比赛 Round #7 B -- Capture(并查集+优先队列)
题意:初始时有个首都1,有n个操作 +V表示有一个新的城市连接到了V号城市 -V表示V号城市断开了连接,同时V的子城市也会断开连接 每次输出在每次操作后到首都1距离最远的城市编号,多个距离相同输出编号 ...
- Redis集群搭建1
wget .168.0.201:6379 192.168.0.201:6380 192.168.0.201:6381 192.168.0.202:16379 192.168.0.202:16380 1 ...
- python学习 2数学公式
递归 def fact(n): if n <= 1: return 1 else: return n * fact(n - 1) 斐波那契数列: 第0项是0,第1项是1,从第2项开始,每一项都等 ...
- 动作手游实时PVP帧同步方案(客户端)
1.概述 1.1.基于UDP的帧同步方案 在技术选型方面,之所以选择帧同步方案,在Kevin的一篇介绍PVP帧同步后台实现的文章中已经做了详细叙述,这里简单摘要如下: 高一致性.如果每一帧的输入都同步 ...
- HDU5800 To My Girlfriend(DP)
题目 Source http://acm.hdu.edu.cn/showproblem.php?pid=5800 Description Dear Guo I never forget the mom ...
- [资料分享]2016 黑马 Java 19期视频+Hadoop大数据实战视频
下载链接: 链接:http://pan.baidu.com/s/1bToXK6 密码:7k43 解压密码: www.lthack.com 或者 2cifang.com 或者 2cifang.com_2 ...
