codeforces 427 div.2 F. Roads in the Kingdom

F. Roads in the Kingdom

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In the Kingdom K., there are n towns numbered with integers from 1 to n. The towns are connected by n bi-directional roads numbered with integers from 1 to n. The i-th road connects the towns u_i and v_i and its length is l_i. There is no more than one road between two towns. Also, there are no roads that connect the towns with itself.

Let's call the inconvenience of the roads the maximum of the shortest distances between all pairs of towns.

Because of lack of money, it was decided to close down one of the roads so that after its removal it is still possible to reach any town from any other. You have to find the minimum possible inconvenience of the roads after closing down one of the roads.

Input

The first line contains the integer n (3 ≤ n ≤ 2·10⁵) — the number of towns and roads.

The next n lines contain the roads description. The i-th from these lines contains three integers u_i, v_i, l_i (1 ≤ u_i, v_i ≤ n, 1 ≤ l_i ≤ 10⁹) — the numbers of towns connected by the i-th road and the length of the i-th road. No road connects a town to itself, no two roads connect the same towns.

It's guaranteed that it's always possible to close down one of the roads so that all the towns are still reachable from each other.

Output

Print a single integer — the minimum possible inconvenience of the roads after the refusal from one of the roads.

Examples

Input

3
1 2 4
2 3 5
1 3 1

Output

5

Input

5
2 3 7
3 1 9
4 1 8
3 5 4
4 5 5

Output

18

题意 ：

　　给定n个点 n条边 （保证联通 ，边无向 ，无重边 ，无自环）

　　断掉某条边以后 保证联通的情况下，图上有一条最长路

　　求最长路的最小值

思路 ：

　　n个联通的点 n条边

　　即 树上多了一个环

　　断掉的边只能在环上

　　所以 题意转化为 从环上断掉一个点以后 树上直径的最小化

　　首先 dfs 找出环

　　然后得到非环上边的最长路（求以环上点为根的子树直径）

　　之后得到环上点到其子树的最长路 记为 点  i  的权值  val [ i ]

　　样例二：

　　　　　　

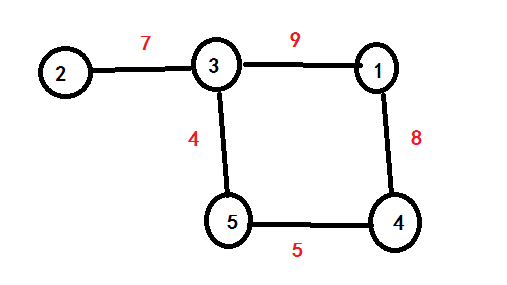
　　得到 当前最长直径是 点 3 的子树  长度为 7   记录下来为   L1  （我在这里错了几次）

　　得到每个点的权值

val   [ 1 ]  =    0

val   [ 3 ]  =    7

val   [ 4 ]  =    0

val   [ 5 ]  =    0

然后得到环上的 前缀路径和 与后缀路径和

　　point     1  ->  3  ->   5  ->  4  ->  1  ->  3  ->  5  ->  4

　　road         9        4        5       8       9       4        5

　　pre- >    0       9        13     18     26      35     39       44  ->

　　suf <-   44       35        31      26      18        9       5       0   <-

　　然后  容易知道  到点 i  的  “前缀和”+ “点权值”  （pre [ i ] + val [ i ]）  表示  环上第一个点（上图中为1）到 i 的 子树的最长路径

　　由于  “树上 离任意一点最远的一定是  直径的某个端点”

　　这样由区间最大值就可以得到 一个直径端点   然后往 “前面” 和 “后面” 找到 离端点最远的另一个点 就是直径的第二个端点

　　每次的区间大小为环的长度 （表示断掉一条边以后的路径前缀和） 每次向右移动一次 得到 第二个直径  并更新 ans

　　区间最大值的维护可以通过线段树      维护一个前缀的  一个后缀的

　　最后答案输出 max（ans,L1)  即可

　　

　　　　

 #include <bits/stdc++.h>

 #define mp make_pair
 #define pb push_back
 #define lson l,mid,pos<<1
 #define rson mid+1,r,pos<<1|1
 #define fi first
 #define se second

 using namespace std;

 typedef long long LL;
 typedef pair<long long ,int> pli;

 const long long INF = 0x3f3f3f3f3f3f3f3f;

 vector <int > nt[];
 vector <int > cc[];
 int noloop[];
 int cnt[];
 LL val[];
 LL toval[];
 LL id[];
 int idfrm[];
 pli tree1[<<];
 pli tree2[<<];
 LL pre[];
 LL suf[];
 int mark=;
 LL zz010=;
 void dfs1(int x,int fa)
 {
     noloop[x]=;
     for (int i=;i<nt[x].size();i++){
         if (fa==nt[x][i])continue;
         cnt[nt[x][i]]--;
         if (cnt[nt[x][i]]==)dfs1(nt[x][i],x);
     }
 }
 LL dfs2(int x,int fa)
 {
     LL ret=;
     LL ret2=;
     for (int i=;i<nt[x].size();i++){
         if (fa==nt[x][i]||noloop[nt[x][i]]==)continue;
         LL tmp=dfs2(nt[x][i],x)+cc[x][i];
         if (tmp>ret){
             ret2=ret;
             ret=tmp;
         }else if (tmp>ret2)ret2=tmp;
     }
     zz010=max(zz010,ret+ret2);
     return val[x]=ret;
 }
 void dfs3(int x,int fa)
 {
     idfrm[mark]=x;
     id[x]=mark;
     for (int i=;i<nt[x].size();i++){
         if (noloop[nt[x][i]]||nt[x][i]==fa||id[nt[x][i]])continue;
         toval[mark++]=cc[x][i];
         dfs3(nt[x][i],x);
         return ;
     }
     for (int i=;i<nt[x].size();i++){
         if (id[nt[x][i]]!=)continue;
         toval[mark]=cc[x][i];
         return ;
     }
 }
 void push_up(pli tree[],int pos)
 {
     tree[pos]=max(tree[pos<<],tree[pos<<|]);
 }
 void upd(pli tree[],int l,int r,int pos,int x,long long val)
 {
     if (l==r){
         tree[pos].fi=val;
         tree[pos].se=x;
         return ;
     }
     int mid=(l+r)>>;
     if (x<=mid)upd(tree,lson,x,val);
     else upd(tree,rson,x,val);
     push_up(tree,pos);
 }
 pli query(pli tree[],int l,int r,int pos,int l1,int r1)
 {
     if (l1>r1)return mp(-INF,);
     if (l>=l1&&r1>=r){
         return tree[pos];
     }
     pli mx=mp(-INF,);
     int mid=(l+r)>>;
     if (mid>=l1)mx=query(tree,lson,l1,r1);
     if (mid+<=r1)mx=max(mx,query(tree,rson,l1,r1));
     return mx;
 }
 int main()
 {
     int n;
     scanf("%d",&n);
     int a,b;
     long long v;
     for (int i=;i<n;i++){
         scanf("%d%d%I64d",&a,&b,&v);
         nt[a].pb(b);
         nt[b].pb(a);
         cc[a].pb(v);
         cc[b].pb(v);
         cnt[a]++;
         cnt[b]++;
     }
     for (int i=;i<=n;i++){
         if (nt[i].size()==)dfs1(i,-);
     }
     for (int i=;i<=n;i++){
         if (noloop[i]==)dfs2(i,-);
     }
     for (int i=;i<=n;i++){
         if (!noloop[i]){
             dfs3(i,-);
             break;
         }
     }
     long long tmp=;
     for (int i=;i<=mark;i++){
         idfrm[i+mark]=idfrm[i];
         toval[i+mark]=toval[i];
     }
     toval[]=toval[mark];
     for (int i=;i<=*mark;i++){
         pre[i]=pre[i-]+toval[i-];
         upd(tree1,,*mark,,i,val[idfrm[i]]+pre[i]);
     }
     for (int i=*mark;i>=;i--){
         suf[i]=suf[i+]+toval[i];
         upd(tree2,,*mark,,i,val[idfrm[i]]+suf[i]);
     }
     LL ans=INF;
     int flag=;
     for (int i=;i<=mark;i++){
         pli now_mx=query(tree1,,*mark,,i,i+mark-);
         pli tmp1=query(tree1,,*mark,,now_mx.se+,i+mark-);
         pli tmp2=query(tree2,,*mark,,i,now_mx.se-);
         LL dis1=0LL,dis2=0LL,dis3=,dis4=;
         if (tmp1.se!=)dis1=val[idfrm[now_mx.se]]+val[idfrm[tmp1.se]]+pre[tmp1.se]-pre[now_mx.se];
         if (tmp2.se!=)dis2=val[idfrm[now_mx.se]]+val[idfrm[tmp2.se]]-pre[tmp2.se]+pre[now_mx.se];
         ans=min(ans,max(dis1,dis2));
     }     cout<<max(ans,zz010);
     return ;
 }

最后   数组记得开大点   前缀和与后缀和  为 环上点数量的两倍