剑指offer（65）：获取数据流中的中位数

参考 https://blog.csdn.net/u011080472/article/details/51291089

题目描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

分析

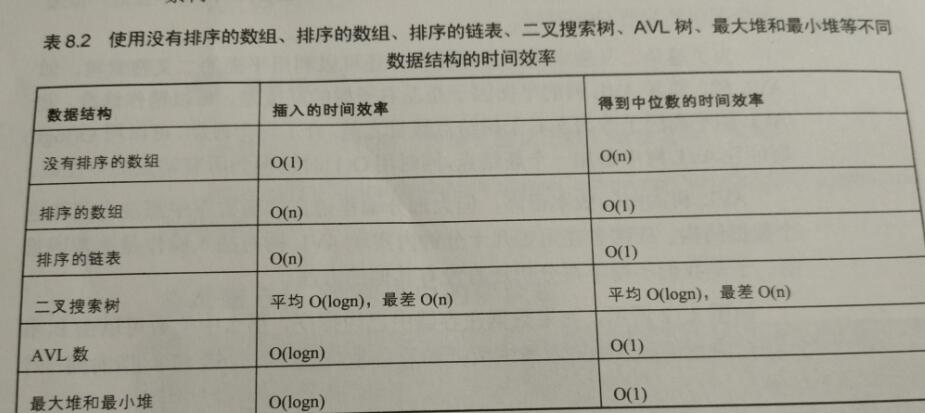
获取中位数有多种方法，但是各种方法的时间效率不一。下面是多种方法的时间复杂度的比较：有图可以知道使用AVL二叉平衡树的方法和使用最大堆最小堆的方法是总的时间复杂度最优的。但是AVL二叉平衡树没有现成的数据结构的实现，因此可以考虑java集合中的PriorityQueue优先队列（也就是堆，默认为小根堆）来实现比较高校的中位数查找。

有关优先队列PriorityQueue，请参考https://www.cnblogs.com/lijingran/p/9143510.html

思路：考虑将数据序列从中间开始分为两个部分，左边部分使用大根堆表示，右边部分使用小根堆存储。每遍历一个数据，计数器count增加1，当count是偶数时，将数据插入小根堆；当count是奇数时，将数据插入大根堆。当所有数据遍历插入完成后（时间复杂度为O(logn)

，如果count最后为偶数，则中位数为大根堆堆顶元素和小根堆堆顶元素和的一半；如果count最后为奇数，则中位数为小根堆堆顶元素。

牛客AC：

import java.util.PriorityQueue;
import java.util.Comparator;

public class Solution {

    private int count = ;  // 数据流中的数据个数
    // 优先队列集合实现了堆，默认实现的小根堆
    private PriorityQueue<Integer> minHeap = new PriorityQueue<>();
    // 定义大根堆，更改比较方式
    private PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(, new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;     // o1 - o2 则是小根堆
        }
    });

    public void Insert(Integer num) {
        if ((count & ) == ) {
            // 当数据总数为偶数时，新加入的元素，应当进入小根堆
            // （注意不是直接进入小根堆，而是经大根堆筛选后取大根堆中最大元素进入小根堆）
            // 1.新加入的元素先入到大根堆，由大根堆筛选出堆中最大的元素
            maxHeap.offer(num);
            int filteredMaxNum = maxHeap.poll();
            // 2.筛选后的【大根堆中的最大元素】进入小根堆
            minHeap.offer(filteredMaxNum);
        } else {
            // 当数据总数为奇数时，新加入的元素，应当进入大根堆
            // （注意不是直接进入大根堆，而是经小根堆筛选后取小根堆中最大元素进入大根堆）
            // 1.新加入的元素先入到小根堆，由小根堆筛选出堆中最小的元素
            minHeap.offer(num);
            int filteredMinNum = minHeap.poll();
            // 2.筛选后的【小根堆中的最小元素】进入小根堆
            maxHeap.offer(filteredMinNum);
        }
        count++;
    }

    public Double GetMedian() {
        // 数目为偶数时，中位数为小根堆堆顶元素与大根堆堆顶元素和的一半
        if ((count & ) == ) {
            return new Double((minHeap.peek() + maxHeap.peek())) / ;
        } else {
            return new Double(minHeap.peek());
        }
    }

}