二叉树终极教程--BinarySearchTree

　　BinarySearchTreeMap的实现

　　

 public interface Map<K extends Comparable<K>, V> {
     void put(K k, V v);

     V get(K k);

     void delete(K k);

     boolean contains(K k);

     boolean isEmpty();

     int size();

     int size(K lo, K hi);

     K min();

     K max();

     K floor(K k);

     K ceiling(K k);

     // the number of keys less than key
     int rank(K k);

     K select(int k);

     void deleteMin();

     void deleteMax();

     // keys in [lo , hi] in sorted order
     Iterable<K> keys(K lo, K hi);

     Iterable<K> keys();
 }

Map　Interface

---

　　二叉树的定义

　　在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。二叉树的左子节点 <  父节点　< 右子节点

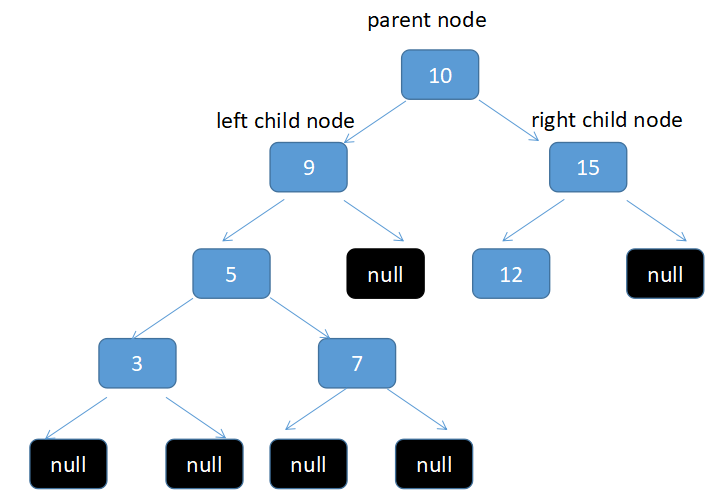
　　这是typical的二叉树的样子, null 代表子节点为空，从这张图可以看出，左子节点 9 小于 父节点 10 小于 右子节点　

　　

     private class Node<K, V> {
         private K k;
         private V v;
         private Node<K, V> left;
         private Node<K, V> right;
         private int size;
         Node(K k, V v) { this.k = k; this.v = v; }
         Node(K k, V v, int size) { this.k = k; this.v = v; this.size = size;}
     }

Node(节点)对象

　　　　　　　　

---

　　 二叉树的插入操作

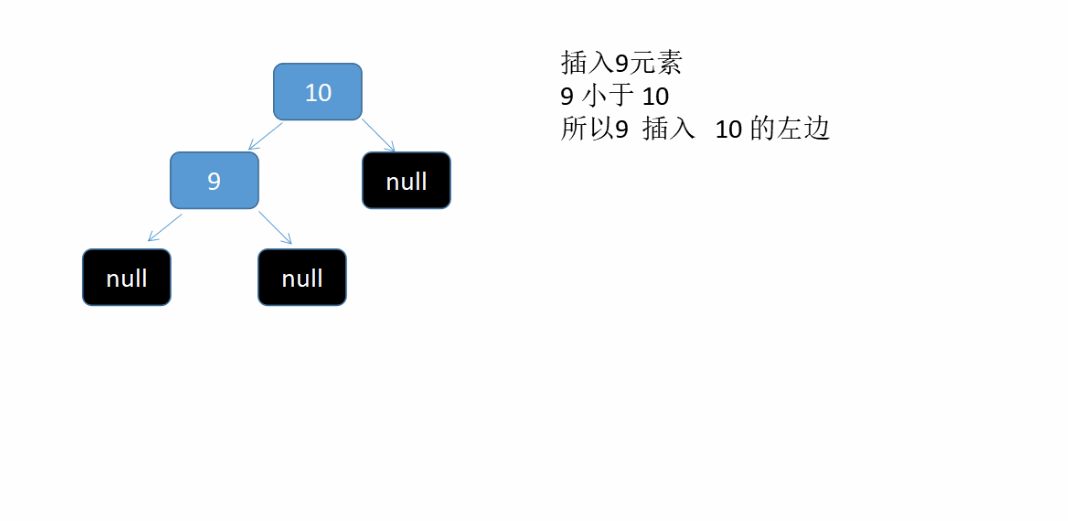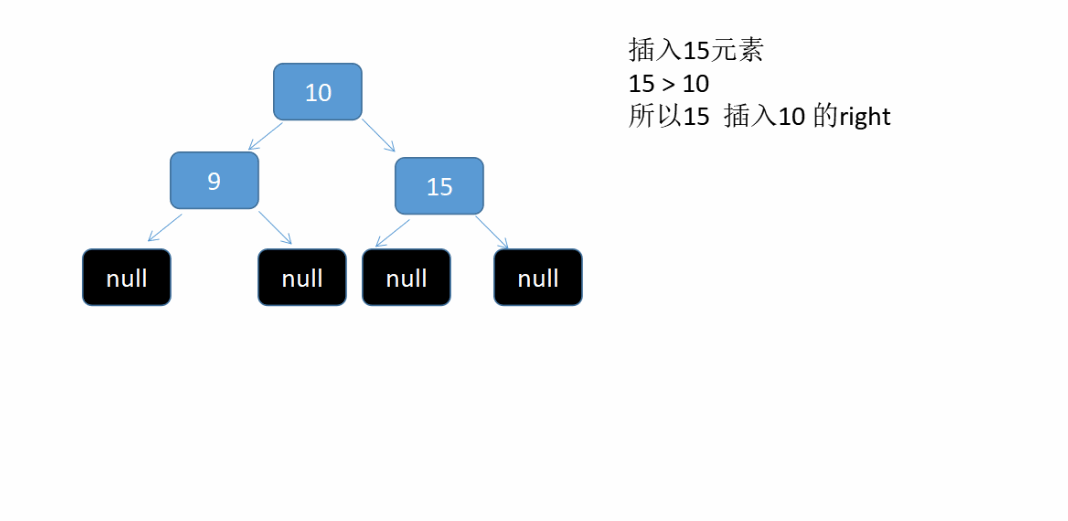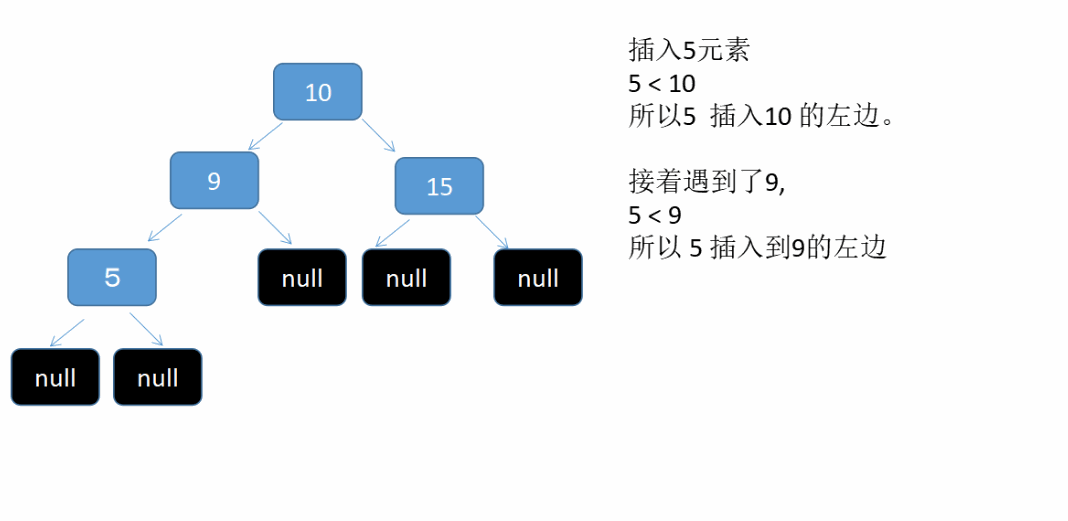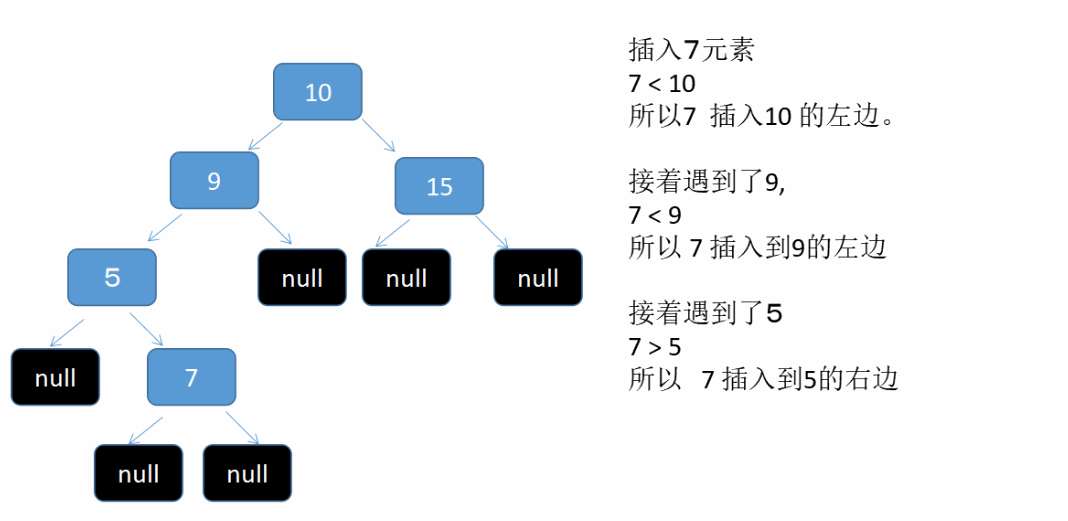
　  假设我们依次插入 10 ， 9， 15， 5 , 7 这5个元素到二叉树中。see what will happen 这是个动态图

     @Override
     public void put(K k, V v) {
         root = put(root, k, v);　//root 是根节点
     }

     private Node<K, V> put(Node<K, V> node, K k, V v) {
         if (node == null) return new Node<>(k, v, 1);
         int cmp = node.k.compareTo(k);
         if (cmp > 0) { //node的k大一点 放到左边的数中
             node.left = put(node.left, k, v);
         } else if (cmp < 0) { //node的k小一点 放到右边的数中
             node.right = put(node.right, k, v);
         } else node.v = v;

         node.size = size(node.left) + size(node.right) + 1;
         return node;
     }

put operation (插入)

---

　　二叉树的get 方法

　　get方法简单来说就是要找到那个key相同的对象。比如我们要在「10 ， 9， 15， 5 , 7 」上图所示中找到　７

　　

　　

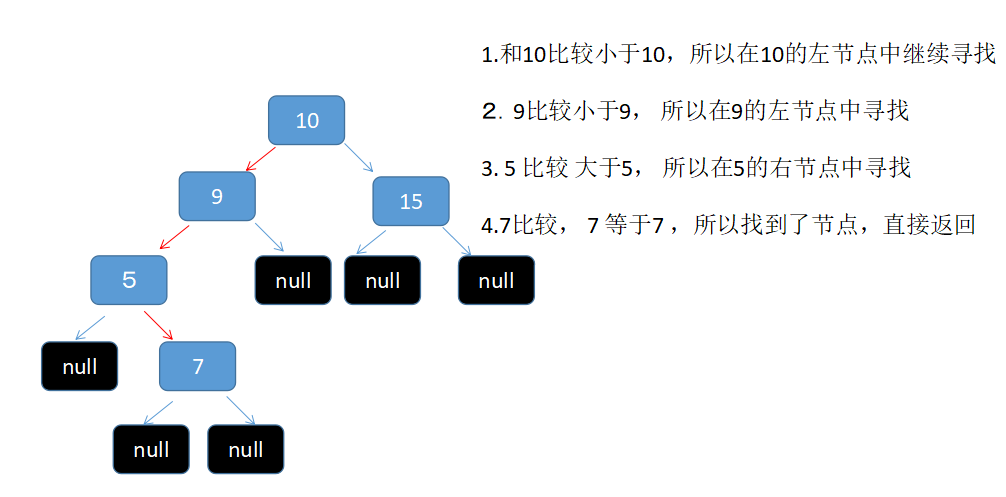
     @Override
     public V get(K k) {
         return get(root, k);
     }

     private V get(Node<K, V> node, K k) {

         if (node == null) return null; //not find
         else if (node.k.compareTo(k) > 0) { //node的k大一点 放到左边的数中
             return get(node.left, k);
         } else if (node.k.compareTo(k) < 0) { //node的k小一点 放到右边的数中
             return get(node.right, k);
         } else {                      //equal
             return node.v;
         }

     }

get operation

　　

---

　　二叉树的删除操作

　　其实想象一下，当你删除一个node的时候，你需要找一个替代node来代替这个node。

　　这里又分3种情况。首先假设你有如下的树结构

　　

　　１．第一种情况是这个删除的节点的左右节点都是null。

　　　　比如我要删除3节点。其实只要直接把3节点reset 为null 就可以了。变成如下

　　

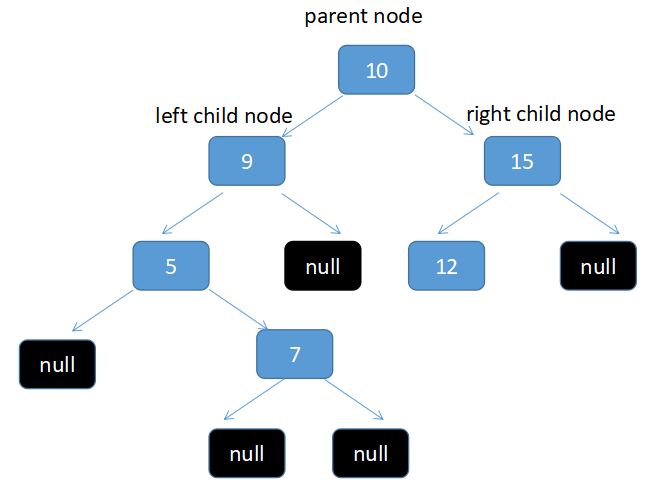
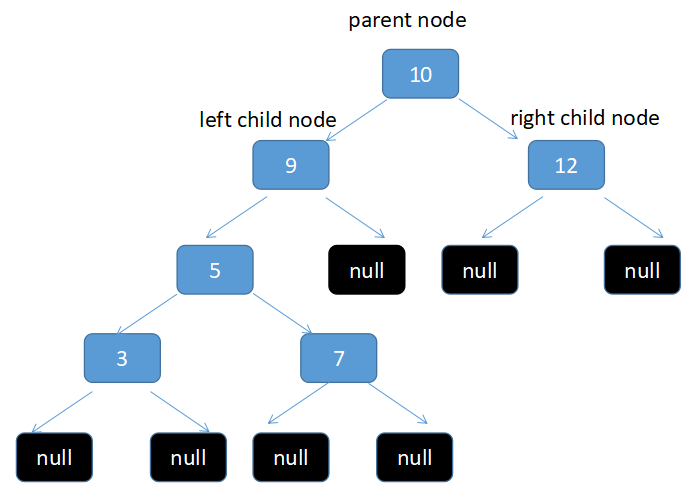
　　　２．第二种情况是删除的节点的2个子节点中有一个子节点为null

　　　　　比如我要删除15。 15 的左节点是12 右节点是 null，所以符合这个情况

　　　　   这个时候只需要直接把需要删除的节点 reset 为 非空的子节点就可以了

所以在这里只需要把15的值替代为12

　　

　　３．第三种情况是删除的节点的2个子节点都不为null，

　　　　这个时候其实可以有2个选择，一个是把删除的节点替换为右子节点为根节点的那个树中最小的节点

　　　　比如我要删除10， 右节点为15（二叉树的删除操作的那个图，不是上面的那个图），15这个节点为根节点的树中总共有2个元素（15和12），12是最小的。所以把需要删除的节点替换为12。删除后如下

　　

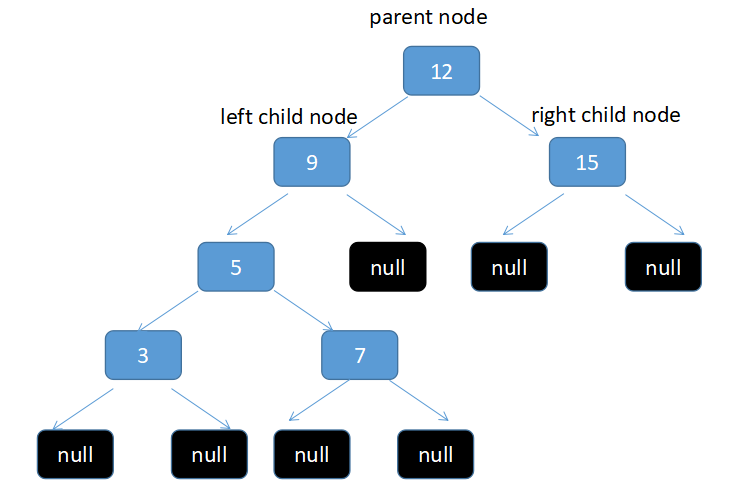
　　　　另外一种选择是把左节点为根节点的树中最大的值取出来，把需要删除的那个节点替换为这个左节点最大的元素（2个选择没什么区别）

　　　　

     @Override
     public void delete(K k) {
         delete(root, k);
     }
     //delete the k in the node tree and reset the size prorperty of this tree and subtrees to correct value
     private Node<K, V> delete(Node<K, V> node, K k) {
         if (node == null) return null;  //没有找到这个node

         int cmp = node.k.compareTo(k);
         if (cmp > 0) {
             node.left = delete(node.left, k);
             node.size = size(node.left) + size(node.right) + 1;
             return node;
         } else if (cmp < 0) {
             node.right = delete(node.right, k);
             node.size = size(node.left) + size(node.right) + 1;
             return node;
         } else {    //hit the key
             if (node.right == null) //if the right node is null then just replace this node with left node
                 return node.left;
             else if (node.left == null) // if the left node is null then just replace this node with right node
                 return node.right;
             else {
                 return deleteMin(node.right); // if both the subnodes are not null replace this node with the smallest node in the right sub node
             }
         }
     }

     //删除从参数node开始的最小的node
     private Node<K, V> deleteMin(Node<K, V> node) {
         return delete(node, min(node));
     }

     private Node<K, V> deleteMax(Node<K, V> node) {
         return delete(node, max(node));
     }

     @Override
     public void deleteMin() {
         deleteMin(root);
     }

     @Override
     public void deleteMax() {
         deleteMax(root);
     }

     @Override
     public K min() {
         return min(root);
     }

     //get the smallest node in the given node
     private K min(Node<K, V> node) {
         if (node == null) return null;
         for (; node.left != null; node = node.left);
         return node.k;
     }

     @Override
     public K max() {
         return max(root);
     }
     //get the most max node in the given node
     private K max(Node<K, V> node) {
         if (node == null) return null;
         for (node = root; node.right != null; node = node.right);
         return node.k;
     }

delete operation 删除操作

---

　　　分析

　　　　BinarySearchTree 有一个最大的缺点，就是如果插入的元素是ordered，比如我插入 1 2 3 4 5  6 这样子，元素都会排在一边。这样子查找起来路径很长，效率很低。

　　　　如果插入的元素是随机的，那么所有的get put 操作的时间复杂度应该是 和　log2(N) 成正比的

　　　　具体的实现可以参考这个。https://github.com/Cheemion/algorithms/blob/master/src/com/algorithms/tree/BinarySearchTreeMap.java

　　　　有什么错误的地方欢迎大家指正哈