hihocoder 网络流二·最大流最小割定理

网络流二·最大流最小割定理

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi：在上一周的Hiho一下中我们初步讲解了网络流的概念以及常规解法，小Ho你还记得内容么？

小Ho：我记得！网络流就是给定了一张图G=(V,E)，以及源点s和汇点t。每一条边e(u,v)具有容量c(u,v)。网络流的最大流问题求解的就是从s到t最多能有多少流量。

小Hi：那这个问题解决办法呢？

小Ho：解决网络流的基本思路就是寻找增广路，不断更新残留网络。直到找不到新的增广路，此时得到的流就是该网络的最大流。

小Hi：没错，看来你记得很牢嘛。

小Ho：哎嘿嘿，不过这里我有一个问题，为什么找不到增广路时就已经找到了最大流呢？

小Hi：这一次我就来解决你的疑惑，首先我们要从网络流的割开始讲起。

对于一个网络流图G=(V,E)，其割的定义为一种点的划分方式：将所有的点划分为S和T=V-S两个部分，其中源点s∈S，汇点t∈T。

对于一个割(S,T)，我们定义净流f(S,T)表示穿过割(S,T)的流量之和，即：

f(S,T) = Σf(u,v) | u∈S,v∈T

举个例子(该例子选自算法导论)：

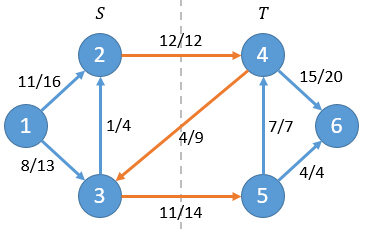
净流f = f(2,4)+f(3,4)+f(3,5) = 12+(-4)+11 = 19

同时我们定义割的容量C(S,T)为所有从S到T的边容量之和，即：

C(S,T) = Σc(u,v) | u∈S,v∈T

同样在上面的例子中，其割的容量为：

c(2,4)+c(3,5)=12+11=23

小Ho：也就是说在计算割(S,T)的净流f(S,T)时可能存在反向的流使得f(u,v)<0，而容量C(S,T)一定是非负数。

小Hi：你这么说也没错。实际上对于任意一个割的净流f(S,T)总是和网络流的流量f相等。比如上面例子中我们改变一下割的方式：

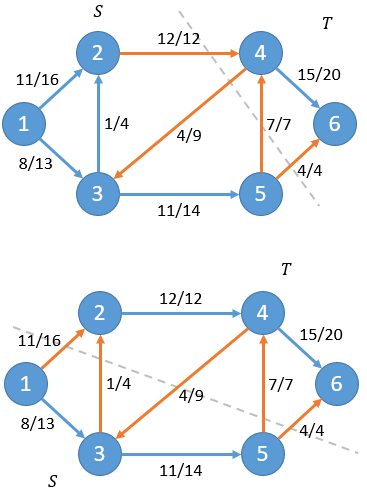
可以计算出对于这两种情况净流f(S,T)仍然等于19。

一个直观的解释是：根据网络流的定义，只有源点s会产生流量，汇点t会接收流量。因此任意非s和t的点u，其净流量一定为0，也即是Σ(f(u,v))=0。而源点s的流量最终都会通过割(S,T)的边到达汇点t，所以网络流的流f等于割的静流f(S,T)。

严格的证明如下：

f(S,T) = f(S,V) - f(S,S)
从S到T的流等于从S到所有节点的流减去从S到S内部节点的流
f(S,T) = f(S,V)
由于S内部的节点之间存在的流一定有对应的反向流，因此f(S,S)=0
f(S,T) = f(s,V) + f(S-s,V)
再将S集合分成源点s和其他属于S的节点
f(S,T) = f(s,V)
由于除了源点s以外其他节点不会产生流，因此f(S-s,V)=0
f(S,T) = f(s,V) = f

所以f(S,T)等于从源点s出来的流，也就是网络的流f。

小Ho：简单理解的话，也就是说任意一个割的净流f(S,T)都等于当前网络的流量f。

小Hi：是这样的。而对于任意一个割的净流f(S,T)一定是小于等于割的容量C(S,T)。那也即是，对于网络的任意一个流f一定是小于等于任意一个割的容量C(S,T)。

而在所有可能的割中，存在一个容量最小的割，我们称其为最小割。

这个最小割限制了一个网络的流f上界，所以有：

对于任一个网络流图来说，其最大流一定是小于等于最小割的。

小Ho：但是这和增广路又有什么关系呢？

小Hi：接下来就是重点了。利用上面讲的知识，我们可以推出一个最大流最小割定理：

对于一个网络流图G=(V,E)，其中有源点s和汇点t，那么下面三个条件是等价的：
1. 流f是图G的最大流
2. 残留网络Gf不存在增广路
3. 对于G的某一个割(S,T)，此时f = C(S,T)

首先证明1 => 2：

我们利用反证法，假设流f是图G的最大流，但是残留网络中还存在有增广路p，其流量为fp。则我们有流f'=f+fp>f。这与f是最大流产生矛盾。

接着证明2 => 3：

假设残留网络Gf不存在增广路，所以在残留网络Gf中不存在路径从s到达t。我们定义S集合为：当前残留网络中s能够到达的点。同时定义T=V-S。
此时(S,T)构成一个割(S,T)。且对于任意的u∈S,v∈T，有f(u,v)=c(u,v)。若f(u,v)<c(u,v)，则有Gf(u,v)>0，s可以到达v，与v属于T矛盾。
因此有f(S,T)=Σf(u,v)=Σc(u,v)=C(S,T)。

最后证明3 => 1：

由于f的上界为最小割，当f到达割的容量时，显然就已经到达最大值，因此f为最大流。

这样就说明了为什么找不到增广路时，所求得的一定是最大流。

小Ho：原来是这样，我明白了。

输入

第1行：2个正整数N,M。2≤N≤500，1≤M≤20,000。

第2..M+1行：每行3个整数u,v,c(u,v)，表示一条边(u,v)及其容量c(u,v)。1≤u,v≤N，0≤c(u,v)≤100。

给定的图中默认源点为1，汇点为N。可能有重复的边。

输出

第1行：2个整数A B，A表示最小割的容量，B表示给定图G最小割S集合的点数。

第2行：B个空格隔开的整数，表示S集合的点编号。

若存在多个最小割可以输出任意一个的解。

样例输入

6 7
1 2 3
1 3 5
2 4 1
3 4 2
3 5 3
4 6 4
5 6 2

样例输出

5 4
1 2 3 5

分析：最小割最大流，dicnic；
代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, rt<<1
#define Rson mid+1, R, rt<<1|1
const int maxn=5e2+;
using namespace std;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
int n,m,k,t,h[maxn],tot,vis[maxn],s,cur[maxn];
bool flag;
set<int>ans;
struct node
{
    int to,nxt,cap,flow;
}e[<<];
void add(int x,int y,int z)
{
    e[tot].to=y;
    e[tot].nxt=h[x];
    e[tot].cap=z;
    h[x]=tot++;
    e[tot].to=x;
    e[tot].nxt=h[y];
    h[y]=tot++;
}
bool bfs()
{
    memset(vis,,sizeof vis);
    queue<int>p;
    p.push(s);
    vis[s]=;
    if(flag)ans.insert(s);
    while(!p.empty())
    {
        int x=p.front();p.pop();
        for(int i=h[x];i!=-;i=e[i].nxt)
        {
            int to=e[i].to,cap=e[i].cap,flow=e[i].flow;
            if(!vis[to]&&cap>flow)
            {
                vis[to]=vis[x]+;
                p.push(to);
                if(flag)ans.insert(to);
            }
        }
    }
    return vis[t];
}
int dfs(int x,int a)
{
    if(x==t||a==)return a;
    int ans=,j;
    for(int&i=cur[x];i!=-;i=e[i].nxt)
    {
        int to=e[i].to,cap=e[i].cap,flow=e[i].flow;
        if(vis[to]==vis[x]+&&(j=dfs(to,min(a,cap-flow)))>)
        {
            e[i].flow+=j;
            e[i^].flow-=j;
            ans+=j;
            a-=j;
            if(a==)break;
        }
    }
    return ans;
}
int max_flow(int s,int t)
{
    int flow=,i;
    while(bfs())
    {
        rep(i,,n)cur[i]=h[i];
        flow+=dfs(s,inf);
    }
    return flow;
}
int main()
{
    int i,j;
    memset(h,-,sizeof h);
    scanf("%d%d",&n,&m);
    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    s=,t=n;
    printf("%d",max_flow(s,t));
    flag=true;
    bfs();
    printf(" %d\n",ans.size());
    for(int x:ans)printf("%d ",x);
    printf("\n");
    //system("Pause");
    return ;
}