hihocoder第42周 3*N骨牌覆盖（状态dp+矩阵快速幂）

http://hihocoder.com/contest/hiho42/problem/1

给定一个n，问我们3*n的矩阵有多少种覆盖的方法

第41周做的骨牌覆盖是2*n的，状态转移方程是dp[i] = dp[i-1] + dp[i-2],递推数列可以用矩阵快速幂来加速计算

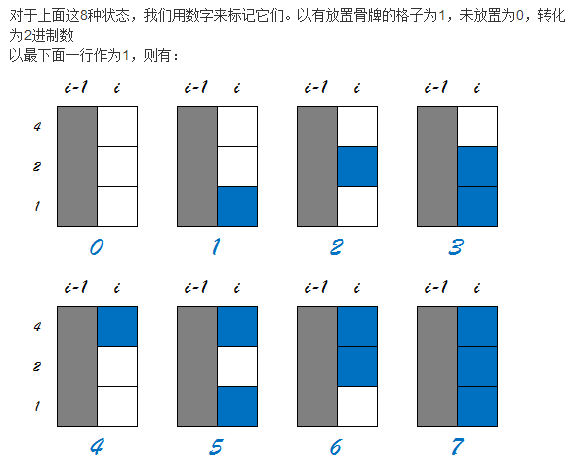
我们可以用状态dp来做这一题，如果某个格子上被铺了骨牌，就标记为1，否则为0

那么每一列一共有8个状态。

两种状态的表示法

第一种：

dp[i][s] 表示填满第i行后，第i+1行的状态为s，

那么s的转移情况如下，

0->1,4,7

1->0,6

2->5

3->4

4->0,3

5->2

6->1

7->0

那么就可以构造出转换的矩阵

 int mat[][] = {
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  }
 };

初始时，只有状态0存在，状态1,2,3,4,5,6,7都不存在

所以初始的向量为 A = [1,0,0,0,0,0,0,0,0]

转换n次后为，  A*mat^n

转化n次后，获得的是第i+1行的不同状态的个数，我们要的是第i+1行状态为0的个数，即A[0]

 #include <stdio.h>
 #include <string.h>
 #include <stdlib.h>
 #include <algorithm>
 #include <iostream>
 #include <queue>
 #include <stack>
 #include <vector>
 #include <map>
 #include <set>
 #include <string>
 #include <math.h>
 using namespace std;
 #pragma warning(disable:4996)
 typedef long long LL;
 const int INF =  << ;
 const int MOD = ;
 /*

 */
 int mat[][] = {
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  }
 };
 int mat2[][] = {
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
     { , , , , , , ,  },
 };
 struct Matrix
 {
     int mat[][];
     Matrix()
     {
         memset(mat, , sizeof(mat));
     }
 };
 Matrix operator*(const Matrix &lhs, const Matrix &rhs)
 {
     Matrix ret;//零矩阵
     for (int i = ; i < ; ++i)
     {
         for (int j = ; j < ; ++j)
         {
             for (int k = ; k < ; ++k)
             {
                 ret.mat[i][j] = (ret.mat[i][j] + lhs.mat[i][k] * rhs.mat[k][j]) % MOD;
             }
         }
     }

     return ret;
 }
 Matrix operator^(Matrix a, int n)
 {
     Matrix ret;//单位矩阵
     for (int i = ; i < ; ++i)
     {
         for (int j = ; j < ; ++j)
             ret.mat[i][j] = mat2[i][j];
     }
     while (n)
     {
         if (n & )
         {
             ret = ret * a;
         }
         n >>= ;
         a = a * a;
     }
     return ret;
 }

 int main()
 {
     int n;
     while (scanf("%d", &n) != EOF)
     {        

         Matrix  a;
         for (int i = ; i < ; ++i)
         {
             for (int j = ; j < ; ++j)
                 a.mat[i][j] = mat[i][j];
         }
         a = a^n;
         cout << a.mat[][] << endl;

     }
     return ;
 }

第二种转换方法为：

dp[i][s]表示填满第i-1行时，第i行的状态为s

同样的，可以得到转化的矩阵， 其实，两种转化的方法就是转化矩阵的不同

 #include <stdio.h>
 #include <string.h>
 #include <stdlib.h>
 #include <algorithm>
 #include <iostream>
 #include <queue>
 #include <stack>
 #include <vector>
 #include <map>
 #include <set>
 #include <string>
 #include <math.h>
 using namespace std;
 #pragma warning(disable:4996)
 typedef long long LL;
 const int INF = <<;
 const int MOD = ;
 /*

 */
 int mat[][] = {
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  }
 };
 int mat2[][] = {
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
         { , , , , , , ,  },
 };
 struct Matrix
 {
     int mat[][];
     Matrix()
     {
         memset(mat, , sizeof(mat));
     }
 };
 Matrix operator*(const Matrix &lhs, const Matrix &rhs)
 {
     Matrix ret;//零矩阵
     for (int i = ; i < ; ++i)
     {
         for (int j = ; j < ; ++j)
         {
             for (int k = ; k < ; ++k)
             {
                 ret.mat[i][j] = (ret.mat[i][j] + lhs.mat[i][k] * rhs.mat[k][j]) % MOD;
             }
         }
     }

     return ret;
 }
 Matrix operator^(Matrix a, int n)
 {
     Matrix ret;//单位矩阵
     for (int i = ; i < ; ++i)
     {
         for (int j = ; j < ; ++j)
             ret.mat[i][j] = mat2[i][j];
     }
     while (n)
     {
         if (n & )
         {
             ret = ret * a;
         }
         n >>= ;
         a = a * a;
     }
     return ret;
 }

 int main()
 {
     int n;
     while (scanf("%d", &n) != EOF)
     {
         n += ;
         Matrix  a;
         for (int i = ; i < ; ++i)
         {
             for (int j = ; j < ; ++j)
                 a.mat[i][j] = mat[i][j];
         }
         a = a^n;
         cout << a.mat[][] << endl;

     }
     return ;
 }