hdu GuGuFishtion 6390 数论 欧拉函数
题目:http://acm.hdu.edu.cn/showproblem.php?pid=6390
直接开始证明:
我们设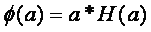 …………………………………….....…...............……………...(1)
…………………………………….....…...............……………...(1)
则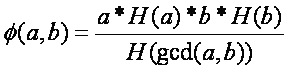 …................................….…(2)
…................................….…(2)
为什么是这样呢,因为我们知道
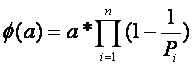
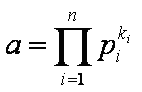
同理得到b的分解和的分解
我们会发现,虽然a和b的分解里可以有相等的部分,但是在里的也就是我们假设为的部分是不会有重复的,那么要由*得出也就是要去除重复部分,的重复部分就是a的和b的的重复部分;那么因为都是乘法,相同的部分就是最大公约数(因为每个都是素数也就是如果a和b的分解没有相同的数那么gcd(, )是不会大于1的);
由此我们开始继续对(2)的后续推论。
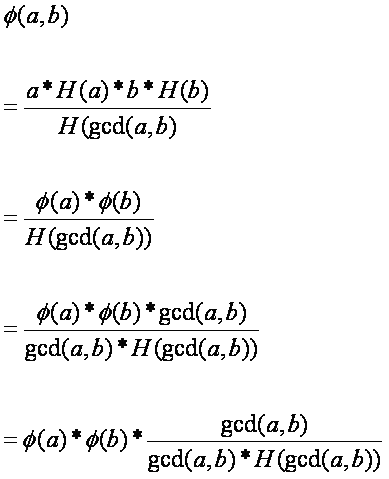
我先设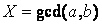 ,那么
,那么
也就是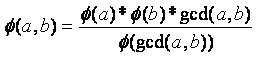
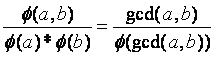 (看了很多博客,就给了个易得,虽然说确实很简单但是对于我这个菜鸡就不友好了)
(看了很多博客,就给了个易得,虽然说确实很简单但是对于我这个菜鸡就不友好了)
这一部分的证明是看了这个大佬的博客的:http://www.cnblogs.com/H-Riven/p/9494391.html
(再提供给同样是数论萌新的人一篇文库【有需要的话】:https://wenku.baidu.com/view/542961fdba0d4a7302763ad5.html)
设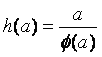
设 (即在
(即在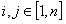 的情况下
的情况下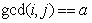 的数量)
的数量)
那么我们实际上就是要求: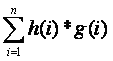 ,对于
,对于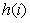 我们可以预处理得到。但是
我们可以预处理得到。但是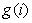 就没那么容易得到了;
就没那么容易得到了;
现在题目就变成求对于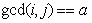 ,在
,在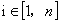 、
、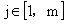 的情况下有多少种方案;
的情况下有多少种方案;
这里我设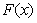 为
为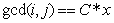 的数量 (C*x表示x的倍数);即可以和HDU1695一样得到
的数量 (C*x表示x的倍数);即可以和HDU1695一样得到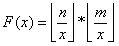 的结论
的结论
设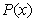 为
为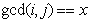 的数量
的数量
那么:
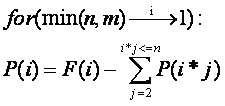
倒过来求的原因是因为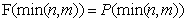 ,也就是我们可以知道最后一位的准确值,那么反过来就可以推到每个位置准确值了;
,也就是我们可以知道最后一位的准确值,那么反过来就可以推到每个位置准确值了;
那么答案就已经出来了;又因为要求的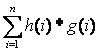 ,对于每个
,对于每个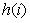 ,是含有有除法的,所以这里要用除法逆元,因为每次的mod都是不同的,所以说每次都要得到逆元,因为
,是含有有除法的,所以这里要用除法逆元,因为每次的mod都是不同的,所以说每次都要得到逆元,因为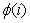 一定会小于min(n,m);所以说每次打从1到 min(n,m)的表比单个值的计算快;
一定会小于min(n,m);所以说每次打从1到 min(n,m)的表比单个值的计算快;
以下是代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e6+;
ll euler[N], inv[N]={, }, F[N], P[N], n, m, mod, mins;
void Euler(){///打欧拉表
register int i, j;
for(i=; i<N; ++i){ euler[i]=i; }
for(i=; i<N; ++i){
if(euler[i]==i){
for(j=i; j<N; j+=i)
euler[j]=euler[j]-euler[j]/i;
}
}
}
void Inv(){///打表求逆元
for(register int i=; i<=mins; ++i){
inv[i]=(ll)(mod-mod/i)*inv[mod%i]%mod;
}
}
int main( ){
Euler();
int T;
register ll ans;
register int i, j;
scanf("%d", &T);
while(T--){
scanf("%I64d%I64d%I64d", &n, &m, &mod);
mins=min(n, m);
Inv();
for(i=; i<=mins; ++i){
F[i]=(n/i)*(m/i)%mod;
}
for(i=mins; i>=; --i){
P[i]=F[i];
for(j=; j*i<=mins; ++j){
P[i]-=P[i*j];
if(P[i]<){
P[i]+=mod;
}
}
}
ans=;
for(i=; i<=mins; ++i){
ans=(ans+(i*inv[euler[i]]%mod)*P[i]%mod)%mod;
}
printf("%I64d\n", ans);
}
}
拙劣的代码
hdu GuGuFishtion 6390 数论 欧拉函数的更多相关文章
- 数论-欧拉函数-LightOJ - 1370
我是知道φ(n)=n-1,n为质数 的,然后给的样例在纸上一算,嗯,好像是找往上最近的质数就行了,而且有些合数的欧拉函数值还会比比它小一点的质数的欧拉函数值要小,所以坚定了往上找最近的质数的决心—— ...
- 【poj 3090】Visible Lattice Points(数论--欧拉函数 找规律求前缀和)
题意:问从(0,0)到(x,y)(0≤x, y≤N)的线段没有与其他整数点相交的点数. 解法:只有 gcd(x,y)=1 时才满足条件,问 N 以前所有的合法点的和,就发现和上一题-- [poj 24 ...
- GuGuFishtion HDU - 6390 (欧拉函数,容斥)
GuGuFishtion \[ Time Limit: 1500 ms\quad Memory Limit: 65536 kB \] 题意 给出定义\(Gu(a, b) = \frac{\phi(ab ...
- HDU 1695 GCD (欧拉函数+容斥原理)
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- BZOJ-2190 仪仗队 数论+欧拉函数(线性筛)
今天zky学长讲数论,上午水,舒爽的不行..后来下午直接while(true){懵逼:}死循全程懵逼....(可怕)Thinking Bear. 2190: [SDOI2008]仪仗队 Time Li ...
- HDU 5430 Reflect(欧拉函数)
题目: http://acm.hdu.edu.cn/showproblem.php?pid=5430 从镜面材质的圆上一点发出一道光线反射NNN次后首次回到起点. 问本质不同的发射的方案数. 输入描述 ...
- hdu 5279 Reflect phi 欧拉函数
Reflect Time Limit: 1 Sec Memory Limit: 256 MB 题目连接 http://bestcoder.hdu.edu.cn/contests/contest_chi ...
- HDU 1695 GCD(欧拉函数+容斥原理)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1695 题意:x位于区间[a, b],y位于区间[c, d],求满足GCD(x, y) = k的(x, ...
- Codeforces_776E: The Holmes Children (数论 欧拉函数)
题目链接 先看题目中给的函数f(n)和g(n) 对于f(n),若自然数对(x,y)满足 x+y=n,且gcd(x,y)=1,则这样的数对对数为f(n) 证明f(n)=phi(n) 设有命题 对任意自然 ...
随机推荐
- ajax请求超时判断(转载)
ajax请求时有个参数可以借鉴一下 var ajaxTimeOut = $.ajax({ url:'', //请求的URL timeout : 1000, //超时时间设置,单位毫秒 type : ' ...
- 关于Backbone和Underscore再说几点
1. Backbone本身没有DOM操作功能,所以我们需要导入JQuery/Zepto/Ender 2. Backbone依赖于underscore.js: http://documentcloud. ...
- 12.17daily_scrum
悬浮窗的优化设计工作已经展开,各界面的测试也在有条不紊的进行,大家都尽量做到了在发现了软件自身的一些问题和bug后,做到在第一时间及时恢复和修改,工作进度的安排也在预期之中,明日的任务发布如下: 具体 ...
- 《Linux内核设计与实现》第一二章读书笔记
第一章 Linux内核简介 1.Unix简介 (一)概念:支持抢占式多任务.多进程.虚拟内存.换页.动态链接和TCP/IP网络的现代化操作系统. (二)Unix特点(层次化结构): Unix很简洁,仅 ...
- c# WndProc事件 消息类型
转载:https://www.cnblogs.com/idben/p/3783997.html WM_NULL = 0x0000; WM_CREATE = 0x0001;应用程序创建一个窗口 WM_D ...
- 对常用软件的评价(TGP腾讯游戏平台)
1,首先说下界面,这款软件的界面有些类似于QQ的界面,登录方式和QQ的方式是一样的,可以简单的说是一款给游戏用的QQ,就是里面的用户变成了游戏 2,功能,简单的说就是将你常玩的游戏放于这游戏平台的表面 ...
- 单片机pc指针
单片机的PC是指程序计数器(Program Counter).程序计数器PC用于存放下一条将要执行的指令地址,是一个16位专用寄存器,不能通过MOV指令来操作,对用户来说是不可见的.当执行一条指令时, ...
- 【Leetcode】222. Count Complete Tree Nodes
Question: Given a complete binary tree, count the number of nodes. Definition of a complete binary t ...
- SVN Update Error: Please execute the 'Cleanup' command
尝试用下面两种方法 svn clean up 中有一个选项break lock勾选上 把对应的文件来里的.svn里面的lock文件删除. svn local delete, incoming dele ...
- jquer导航锚点链接动画效果和返回顶部代码
$(function(){ $(".index_nav li a").click(function(event){ //绑定按钮的单击事件 var index = this.tit ...
