bzoj千题计划205：bzoj3529: [Sdoi2014]数表

http://www.lydsy.com/JudgeOnline/problem.php?id=3529

有一张n*m的数表，其第i行第j列（1 < =i < =n，1 < =j < =m）的数值为能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。

20000 组询问  n<=1e5

f（k）表示 k 的 约数和

g（k）表示 

f（k）的求法：

http://www.cnblogs.com/TheRoadToTheGold/p/8228969.html

g（k）的求法：

http://www.cnblogs.com/TheRoadToTheGold/p/6609495.html

假设没有a的限制

不妨令n<=m

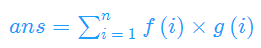
即

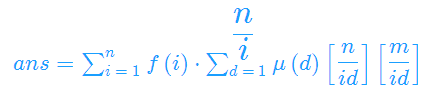
令i*d=t，把后面两个下取整提到前面

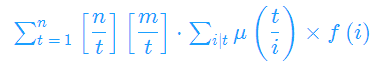
令

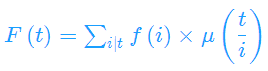
则

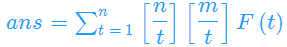
预处理出F(t)，除法分块便可以在O（sqrt(n)）求解

但是现在有f(i)<=a 的限制

离线处理，读入所有的询问

所以把f(i)按f(i)的值从小到大排序

询问按a的值从小到大排序

用树状数组维护当前F(t)的值

在处理这个询问之前

找出所有<=本次询问a的f(i)

在树状数组中i及i的倍数位置加上f(i)

取模不用管，自然溢出即可

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

#define N 100001
#define M 20001

typedef long long LL;

int T;

int miu[N];

int p[N];
bool vis[N];

struct nodef
{
    int d,val;
}f[N];
int c[N];

bool cmpf(nodef A,nodef B)
{
    if(A.val!=B.val) return A.val<B.val;
    return A.d<B.d;
}

struct Query
{
    int id;
    int n,m,a;
}Q[M];

bool cmpQ(Query A,Query B)
{
    return A.a<B.a;
}

int ans[M];

struct BIT
{
    int s[N];

    #define lowbit(x) x&-x

    void add(int x,int val)
    {
        while(x<N-)
        {
            s[x]=s[x]+val;
            x+=lowbit(x);
        }
    }

    int query(int x)
    {
        int sum=;
        while(x)
        {
            sum=sum+s[x];
            x-=lowbit(x);
        }
        return sum;
    }

}Bit;

void read(int &x)
{
    x=; int f=; char c=getchar();
    while(!isdigit(c)) { if(c=='-') f=-; c=getchar(); }
    while(isdigit(c))  { x=x*+c-''; c=getchar(); }
    x*=f;
}

void pref()
{
    int cnt=;
    miu[]=;
    f[].d=;
    f[].val=;
    for(int i=;i<N;++i)
    {
        f[i].d=i;
        if(!vis[i])
        {
            p[++cnt]=i;
            miu[i]=-;
            f[i].val=i+;
            c[i]=;
        }
        for(int j=;j<=cnt;++j)
        {
            if(i*p[j]>=N) break;
            vis[i*p[j]]=true;
            if(i%p[j]==)
            {
                f[i*p[j]].val=f[i].val*p[j]+c[i];
                c[i*p[j]]=c[i];
                break;
            }
            miu[i*p[j]]=-miu[i];
            f[i*p[j]].val=f[i].val*(p[j]+);
            c[i*p[j]]=f[i].val;
        }
    }
    sort(f+,f+N,cmpf);
}

void init()
{
    read(T);
    for(int i=;i<=T;++i)
    {
        read(Q[i].n);
        read(Q[i].m);
        read(Q[i].a);
        Q[i].id=i;
    }
    sort(Q+,Q+T+,cmpQ);
}

void solve()
{
    int nowQ=;
    while(Q[nowQ].a<=) nowQ++;
    int nowd=;
    int j,res;
    int tot,lastsum,nowsum;
    for(;nowQ<=T;++nowQ)
    {
        while(nowd<N && f[nowd].val<=Q[nowQ].a)
        {
            for(int i=f[nowd].d;i<N;i+=f[nowd].d)
                Bit.add(i,f[nowd].val*miu[i/f[nowd].d]);
            nowd++;
        }
        if(Q[nowQ].n>Q[nowQ].m) swap(Q[nowQ].n,Q[nowQ].m);
        tot=lastsum=;
        for(int i=;i<=Q[nowQ].n;i=j+)
        {
            j=min(Q[nowQ].n/(Q[nowQ].n/i),Q[nowQ].m/(Q[nowQ].m/i));
            nowsum=Bit.query(j);
            res=nowsum-lastsum;
            res=res*(Q[nowQ].n/i)*(Q[nowQ].m/i);
            tot+=res;
            lastsum=nowsum;
        }
        tot+= tot< ? 1LL<< : ;
        ans[Q[nowQ].id]=tot;
    }
    for(int i=;i<=T;++i) cout<<ans[i]<<'\n';
}

int main()
{
    pref();
    init();
    solve();
}