NLP自然语言处理系列5-支持向量机(SVM)

1.什么是支持向量机

　　支持向量机（Support Vector Machine，SVM）是一种经典的分类模型，在早期的文档分类等领域有一定的应用。了解SVM的推导过程是一个充满乐趣和挑战的过程，耐心的看完整个过程，你会受益良多。所以，小Dream也决定好好讲一讲SVM的推导过程，还是跟此前一样，讲解务必追求通俗易懂，深入浅出。

　　首先要说的是，支持向量机最主要是用于分类。假设有一个训练样本集D={（x₁,y₁），（x₂,y₂），（x₃,y₃），...（x_n,y_n）}，支持向量机分类学习最主要的思想就是基于训练集D在样本空间中，找到一个划分超平面，将不同类别的样本分开。

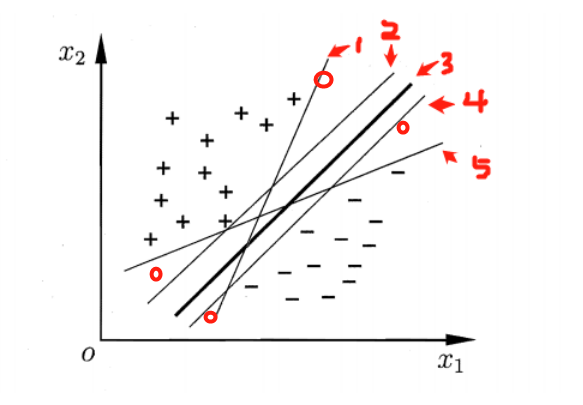
图一类别划分超平面

　　如图一所示，那些能够将+、-两类样本分开的直线（超平面），都是合理的分类器。那么，哪个分类器是最优的呢？我们可以看到，当一个新的样本（样本可能有扰动）出现在图中4个红色圆圈所在位置时，分类器1，2，4，5就极有可能把他分错。根据图一，肉眼可见，分类器3是图中的最优分类器，因为它忍受样本干扰的能力是最强的，用术语说，就是最鲁棒的。那么怎么从数学上来定义这个最优的超平面呢？

　　在样本空间中，假设划分超平面是这样的一个平面：

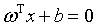（1）

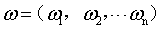　　称为超平面的法向量，b定义了超平面到空间远点的距离，回忆一下高中的立体几何，我们知道，超平面可以由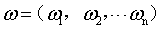和b唯一确定。那么。怎么样的一个超平面是最优的呢？

　　首先，我问这样一个问题，样本空间中任意一个样本，到该划分超平面的距离应该怎么表示？（赶紧回忆一下，点到平面的距离

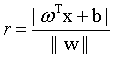　（2）

　　我们先假设超平面能够将所有的样本正确的进行分类。对任意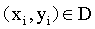如果样本属于正类，则有y_i=+1，且；如果样本属于负类，则有y_i=-1，且。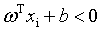

　　我们可以选择合适的b，使得离超平面最近的哪一类点满足如下的条件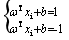：，这些点就称为支持向量。那么所有样本可以这样表示：

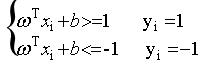（3）

　　如图二所示，支持向量用圈圈圈住了。两个异类的支持向量的距离可以表示为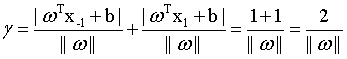：（4）

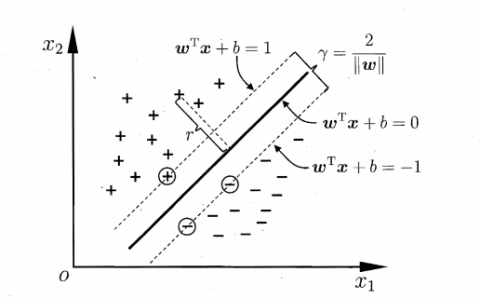　　图二支持向量与间隔

　　那么选择最优的划分超平面就可以转为成如下的数学表达式：

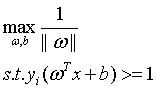　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (5)

　　为了计算简便，（5）式等价于如下：

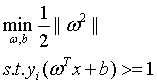　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（6）

　　怎么样，这就是SVM的基本型了，有没有感受到数学语言的魅力？简洁、明确而又优美。

2. 支持向量机如何学习

　　既然我们明确了SVM是个怎么样的问题，接下来要考虑的就是如何利用数据集D求得上述的超平面。

　　我们期望根据式6，获得一个模型：

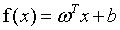　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (7)

　　式6是一个凸二次规划问题，可能会有相关的优化计算包可以求解。但是SVM有自己的更为高效的求解方式，我们来好好说一下。

　　求解这种带限制条件的极值问题，用的最多的应该式拉格朗日乘子法。我们对式6的每个约束条件乘以拉格朗日乘子: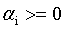

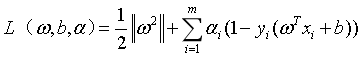　　　　　　　　　　　　　　　　　　 (8)

　　其中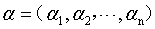为拉格朗日乘子向量，注意向量的长度和数据集D中样本的数目相同。根据拉格朗日极值法，分别对w和b求偏导，并取极值得到：

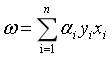　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (9)

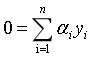　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (10)

　　将式（9）（10）带入式（8），可以得到：

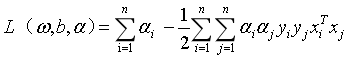
　　参考https://blog.csdn.net/zlsjsj/article/details/80522650

　　我们可以得到式6的对偶问题：

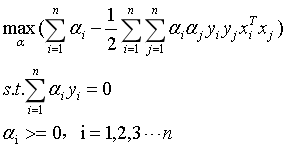　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(11)

　　这么多公式，相信大家看到都有点烦了，这里总结一下，理一理思路。

　　我们得到式6的SVM基本型之后，想要用一种高效的方式来求解SVM的划分超平面。在限定条件下的极值问题，我们想到了拉格朗日乘子法。通过求偏导、解极值之后，我们消去w和b，问题变成了解决式6的对偶问题式11。这样的话，求解w和b就转化成了求解拉格朗日乘子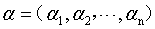。将所有拉格朗日乘子求出之后，就得到了模型：

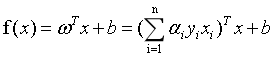
　　这里我们注意，拉格朗日乘子的个数与数据集样本的个数相同。

　　那么，式11该如何高效的求解呢？下面我们SMO（Sequential Minimal Optimization）算法就登场了。

　　SMO算法的基本思路是各个击破，逐个参数优化求解。具体来说就是，先选定一个参数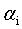，然后固定除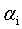之外的所有其他参数，这样就可以根据式11求极值，求得合适的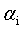。具体来说，是这样的，先选定两个参数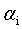和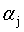，根据式11的限制条件会有：

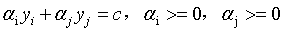　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (12)

　　其中，。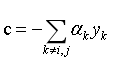

　　可以用式12将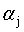用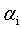来表示，带入到式11中，得到一个关于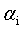的单变量二次规划（二次函数求极值）问题，就可以高效的进行求解了。

2. SVM中的核函数

　　上述的SVM问题的定义及求解过程中，隐含了一个假设，就是存在一个超平面，能够将两类样本分开，即问题是线性可分的。那么，如果问题不是线性可分的呢？例如，很简答的“异或”问题就是线性不可分的。

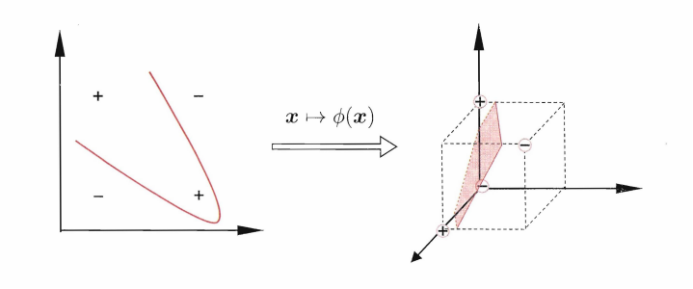
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　图三线性不可分问题及其非线性映射

　　如图三所示，在二维空间中，没有办法找到一条直线，将“异或”问题进行正确的区分。那么如何解决线性不可分的问题呢？在图三中，将四个样本经过一个映射函数，映射到三维空间中，就可以通过一个平面将该问题划分开了。

　　这样我们就有了利用SVM去分类线性不可分问题的思路了。我们可以通过一个映射函数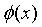，将样本从原空间映射到高维空间，再利用上面章节的SVM原理进行分类就可以了。

　　下面我们再简单说一下利用升维的办法用SVM进行分类的过程。

　　训练样本集经过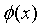进行映射，变成了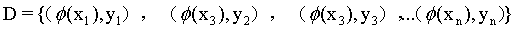，那么我们要获得这样一个模型：

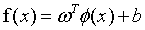　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（13）

　　在如下的限制条件下：

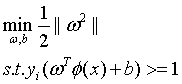　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（14）

　　同样，得到它的对偶问题：

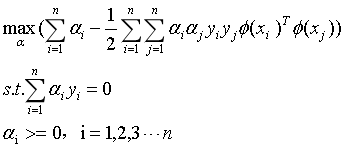　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（15）

　　同样，问题的本质并没有改变，我们其实还是可以用SMO算法求解向量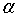。只是多了一步，要计算，当样本空间的维度很大时，这个计算量时很大的。为了简化计算，我们聪明的算法专家提出了核函数的概念，所谓核函数，就是为了简化上述计算而设计出来的函数，它满足如下要求：

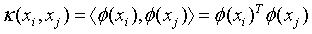　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（16）

　　那么式15就可以改写为：

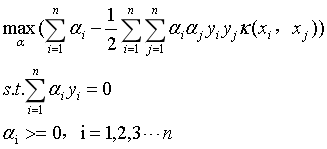　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（17）

　　我们仔细回顾下抑或问题的映射过程，可以发现，其实映射过程不是唯一的，只要满足一定的性质，映射函数可以很多，同样核函数也可以很多。

　　我们先列出来常用的核函数：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　图四常用核函数列表

　　那么，加入我们使用的高斯核，则式17可以表示为：

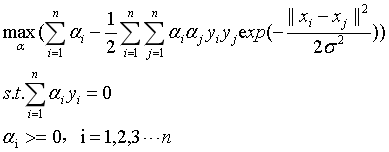　　　　　　　　　　　　　　　　　　　　　　　　（18）

　　我们可以看到加入核函数后，能够顺利解决线性不可分的问题，但是计算过程却并没有因此而变得复杂。

　　关于核函数的选择以及过拟合的处理，可以用软间隔的技术，大体的思想就是在最大化间隔的同时，允许一些样本出现在间隔里。感兴趣的同学可以出门百度一下，这里不再详述。

　　这篇博客可能没有太多原创的思考，但是都是小Dream根据自己的理解一个字一个字码的，可能在遣词造句上没有教科书那么严谨。但是我觉得技术博客存在意义就在于用一种朴实易懂的语言介绍一些在实际工作中非常实用的技巧、经验和技术。

---------------------------------------------------------------------------------------------------------------------------------

分享时刻：

　　你要记住，人生聚散起伏太常见。生命太短，铭记那些温暖与真诚吧，倒掉那些凉掉的茶水。