昨天，刚接触道了李群和李代数，查了许多资料，也看了一些视屏。今天来谈谈自己的感受。

李群是有一个挪威数学家提出的，在十九二十世纪得到了很大的发展。

其归于非组合数学，现在简单介绍李群和李代数的概念。群的定义是一种集合加上一种运算的代数结构。其集合记为A，运算记为 . ,当其满足以下四条性质时，就称其为（A,.）群。

为了大家更好的理解，我还是放上讲师（高博slam十四讲其四）的ppt吧。

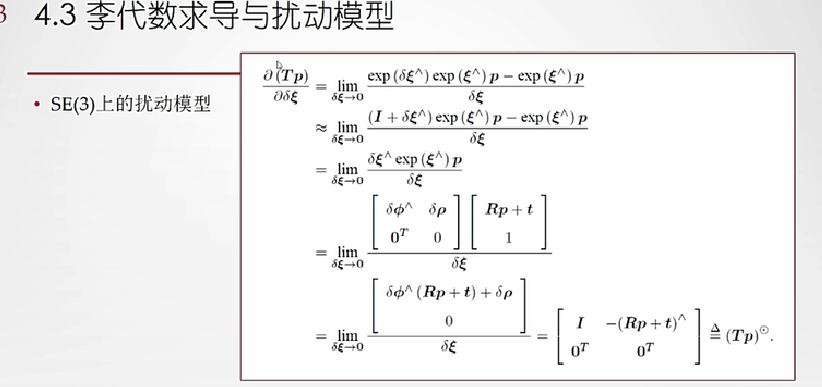
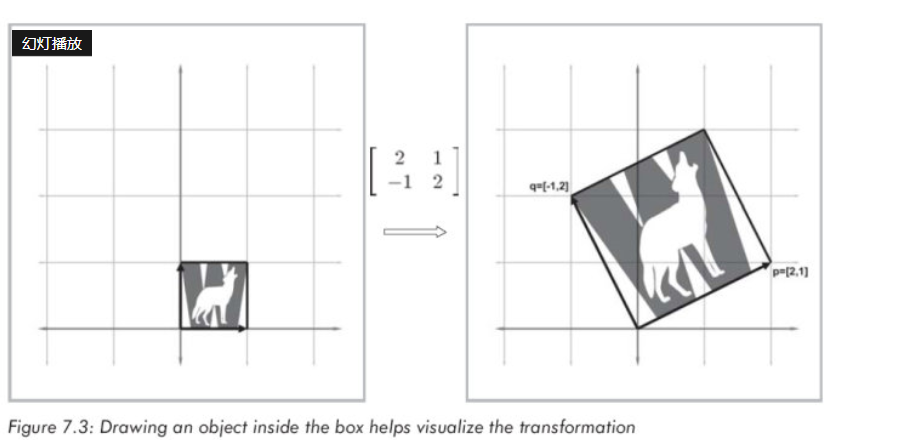
矩阵旋转

李群与李代数在slam中的应用的更多相关文章

  1. 视觉SLAM中的数学基础 第四篇 李群与李代数（2）

    前言 理解李群与李代数,是理解许多SLAM中关键问题的基础.本讲我们继续介绍李群李代数的相关知识,重点放在李群李代数的微积分上,这对解决姿态估计问题具有重要意义. 回顾 为了描述三维空间里的运动,我们 ...

  2. 视觉SLAM中的数学基础 第三篇 李群与李代数

    视觉SLAM中的数学基础 第三篇 李群与李代数 前言 在SLAM中,除了表达3D旋转与位移之外,我们还要对它们进行估计,因为SLAM整个过程就是在不断地估计机器人的位姿与地图.为了做这件事,需要对变换 ...

  3. 从零开始一起学习SLAM | 为啥需要李群与李代数？

    很多刚刚接触SLAM的小伙伴在看到李群和李代数这部分的时候,都有点蒙蒙哒,感觉突然到了另外一个世界,很多都不自觉的跳过了,但是这里必须强调一点,这部分在后续SLAM的学习中其实是非常重要的基础,不信你 ...

  4. SLAM中的EKF，UKF，PF原理简介

    这是我在知乎上问题写的答案,修改了一下排版,转到博客里.   原问题: 能否简单并且易懂地介绍一下多个基于滤波方法的SLAM算法原理? 目前SLAM后端都开始用优化的方法来做,题主想要了解一下之前基于 ...

  5. SLAM中的优化理论（一）—— 线性最小二乘

    最近想写一篇系列博客比较系统的解释一下 SLAM 中运用到的优化理论相关内容,包括线性最小二乘.非线性最小二乘.最小二乘工具的使用.最大似然与最小二 乘的关系以及矩阵的稀疏性等内容.一方面是督促自己对 ...

  6. SLAM中的优化理论（二）- 非线性最小二乘

    本篇博客为系列博客第二篇,主要介绍非线性最小二乘相关内容,线性最小二乘介绍请参见SLAM中的优化理论(一)-- 线性最小二乘.本篇博客期望通过下降法和信任区域法引出高斯牛顿和LM两种常用的非线性优化方 ...

  7. 视觉SLAM中相机详解

    视觉SLAM中,通常是指使用相机来解决定位和建图问题. SLAM中使用的相机往往更加简单,不携带昂贵的镜头,以一定的速率拍摄周围的环境,形成一个连续的视频流. 相机分类: 单目相机:只是用一个摄像头进 ...

  8. SLAM中的变换（旋转与位移）表示方法

    1.旋转矩阵 注:旋转矩阵标题下涉及到的SLAM均不包含位移. 根据同一点P在不同坐标系下e(e1,e2,e3)e'(e1',e2',e3')的坐标a(a1,a2,a3)a'(a1',a2',a3') ...

  9. 视觉SLAM中的数学基础 第二篇 四元数

    视觉SLAM中的数学基础 第二篇 四元数 什么是四元数 相比欧拉角,四元数(Quaternion)则是一种紧凑.易于迭代.又不会出现奇异值的表示方法.它在程序中广为使用,例如ROS和几个著名的SLAM ...

随机推荐

  1. Java语言的主要特点

    Java语言有很多的优点,可靠.安全.编译和解释型语言.分布式.多线程.完全面向对象.与平台无关性等等. 与平台无关性 Java语言最大的优势在于与平台无关性,也就是可以跨平台使用. 绝大多数的编程语 ...

  2. 怎么查看自己电脑的IP地址

    1/2 使用Windows+R键打开“运行”窗口,然后输入CMD进入命令提示窗口 进入命令窗口之后,输入:ipconfig/all 回车即可看到整个电脑的详细的IP配置信息 1/3 使用网络状态查看I ...

  3. 数据库迁移之从oracle 到 MySQL最简单的方法

    数据库迁移之从oracle 到 MySQL最简单的方法 因工作需要将oracle数据库换到MySQL数据库,数据量比较大,百万级别的数据,表也比较多,有没有一种既快捷又安全的方法呢?答案是肯定的,下面 ...

  4. Docker容器学习与分享02

    1.docker容器的创建 首先运行一个centos容器,感受一下Docker容器的便捷 首先先看一下镜像仓库 发现仓库里没有镜像,也就是没有创建容器的模板,这时考虑从REPOSITORY中拉取镜像( ...

  5. XtraEditors七、ProgressBarControl、MarqueeProgressBarControl、ProgressPanel控件

    一.ProgressBarControl 进度条控件 效果如下: 示例代码: using System; using System.Collections.Generic; using System. ...

  6. 【转】为什么Github没有记录你的Contributions

    【转】为什么Github没有记录你的Contributions 字数985 阅读0 评论0 喜欢0 记录下为什么github 提交的时候，没有记录到 github 的那个日历上。 Paste_Imag ...

  7. 【Python求助】在eclipse和pycharm中，通过adb install安装中文名字APK时老是报错，如何解决

    # -*- coding: utf-8 -*- import os import sys import subprocess import time from uiautomator import d ...

  8. SecureCRT Win免安装版本，简单好用

    SecureCRT是一款支持SSH(SSH1和SSH2)的终端仿真程序,简单地说是Windows下登录UNIX或Linux服务器主机的软件. 这个简单好用,程序员必备. 下载地址:SecureCRT. ...

  9. 使用java实现hex和ascii码的转换

    几乎很少写JAVA代码,第一是确实不会,第二感觉JAVA写起来不爽(较python.golang),但总有万不得已必须要用java的时候.这里记录下使用java实现的hex十六进制和acsii码之间的 ...

  10. PAT A1009 Product of Polynomials （25 分）——浮点，结构体数组

    This time, you are supposed to find A×B where A and B are two polynomials. Input Specification: Each ...