StanFord ML 笔记 第四部分

---

第四部分：

　　　　1.生成学习法 generate learning algorithm

　　　　2.高斯判别分析 Gaussian Discriminant Analysis

　　　　3.朴素贝叶斯 Navie Bayes

　　　　4.拉普拉斯平滑 Navie Bayes

---

一、生成学习法generate learning algorithm：

　　　　二类分类问题，不管是感知器算法还是逻辑斯蒂回归算法，都是在解空间中寻找一条直线从而把两种类别的样例分开，对于新的样例只要判断在直线的哪一侧即可；这种直接对问题求解的方法可以成为判别学习方法（discriminative learning algorithm）。而生成学习算法则是对两个类别分别进行建模，用新的样例去匹配两个模型，匹配度较高的作为新样例的类别，比如良性肿瘤与恶性肿瘤的分类，首先对两个类别分别建模，比如分别计算两类肿瘤是否扩散的概率，计算肿瘤大小大于某个值的概率等等；再比如狗与大象的分类，分别对狗与大象建模，比如计算体重大于某个值的概率，鼻子长度大于某个值的概率等等。

比如说良性肿瘤和恶性肿瘤的问题，对良性肿瘤建立model1（y=0），对恶性肿瘤建立model2（y=1），p(x|y=0)表示是良性肿瘤的概率,p(x|y=1)表示是恶性肿瘤的概率.

根据贝叶斯公式（Bayes rule）推导出y在给定x的概率为：

　　　　注释如下：

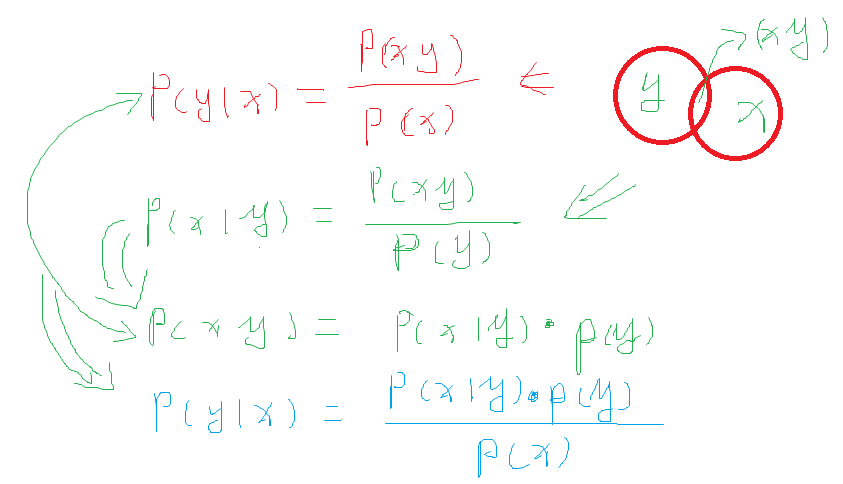
二、高斯判别分析 Gaussian Discriminant Analysis：

　　　　

　　　　先看概念：高维高斯分布的理解

　　1. 如何描述问题？

　　1.0 问题的假设是什么？

　　　　这个模型对于数据有非常强的假设：

　　　　它假设变量是连续的，并且每一个特征都符合正态分布（即高斯分布）

　　　　即输入特征满足多元正态分布（后面来讲）

　　　　对应一个二元分类问题 y = h(x), 需要满足下面的分布：

　　1.1 如何用模型描述问题？ 

　　　　由于有了上面的假设，问题可以描述为：

　　　　当需要分类是，通过贝叶斯公式计算其属于某一类的概率：

　　1.2 如何定义求解目标？

　　　　算法的求解目标为使其联合概率最大化，即

　　2. 如何求解问题？

　　　　对似然函数求导得到

　　　　算法表述在图上可以为

　　什么是多元正态分布（The Multivariate Normal Distribution）？

　　　　多元正态分布描述的是 n 维随机变量的分布情况,这里的μ变成了向量,  σ也变成了矩阵Σ。写作