JZYZOJ 2042 多项式逆元 NTT 多项式

http://172.20.6.3/Problem_Show.asp?id=2042

题意：求一个次数界为n的多项式在模P并模x^m的意义下的逆元。P=7*17*2^23+1。

多项式逆元的含义以及求逆元的方法：http://blog.miskcoo.com/2015/05/polynomial-inverse

公式推导一下。主要还是NTT的使用，我NTT写错了调了半天，太zz了。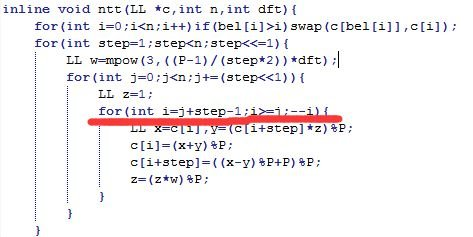

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #include<complex>
 using namespace std;
 #define LL long long
 const LL P=(LL)**(<<)+;
 const int maxn=;
 LL a[maxn]={},b[maxn]={},e[maxn]={},zz[][maxn]={};
 int bel[maxn]={};
 int bt,s,tot=;
 LL mpow(LL x,LL k){
     if(k<){x=mpow(x,P-);k=-k;}
     LL z=;
     while(k){
         if(k&)z=(z*x)%P;
         x=(x*x)%P;
         k/=;
     }return z;
 }
 inline void getit(){ for(int i=;i<s;i++)bel[i]=((bel[i>>]>>)|((i&)<<(bt-))); }
 inline void ntt(LL *c,int n,int dft){
     for(int i=;i<n;i++)if(bel[i]>i)swap(c[bel[i]],c[i]);
     for(int step=;step<n;step<<=){
         LL w=mpow(,((P-)/(step*))*dft);
         for(int j=;j<n;j+=(step<<)){
             LL z=;
             for(int i=j;i<j+step;++i){
                 LL x=c[i],y=(c[i+step]*z)%P;
                 c[i]=(x+y)%P;
                 c[i+step]=((x-y)%P+P)%P;
                 z=(z*w)%P;
             }
         }
     }
     if(dft==-){
         LL mon=mpow(n,P-);
         for(int i=;i<n;i++)c[i]=(c[i]*mon)%P;
     }
 }
 inline void dontt(LL *c,LL *d,int x,int y){
     bt=;s=;int z=x+y-;
     for(;s<z;++bt)s<<=;
     getit();
     ntt(c,s,);ntt(d,s,);
     for(int i=;i<s;i++)c[i]=(c[i]*d[i])%P;
     ntt(c,s,-);ntt(d,s,);
 }
 inline void doit(int n,int m){
     if(m==){++tot; zz[tot][]=mpow(a[],P-); return ;}
     doit(n,(m+)/);int siz=(m+)/; ++tot;
     for(int i=;i<s;i++)e[i]=b[i]=bel[i]=;
     for(int i=;i<siz;i++){zz[tot][i]=(zz[tot-][i]*)%P;b[i]=zz[tot-][i];}
     for(int i=min(n,m)-;i>=;--i)e[i]=a[i];
     dontt(zz[tot-],b,siz,siz); siz=siz+siz-;
     dontt(zz[tot-],e,siz,min(n,m));
     for(int i=;i<m;i++)zz[tot][i]=((zz[tot][i]-zz[tot-][i])%P+P)%P;
 }
 int main(){
     //freopen("a.in","r",stdin);
     int n,m;scanf("%d%d",&n,&m);
     for(int i=;i<n;i++){scanf("%lld",&a[i]);a[i]=((a[i]%P)+P)%P;}
     doit(n,m);
     for(int i=;i<m;i++)printf("%lld ",zz[tot][i]);
     printf("\n");
     return ;
 }