洛谷 P1043 数字游戏 区间DP

题目描述

丁丁最近沉迷于一个数字游戏之中。这个游戏看似简单，但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。游戏是这样的，在你面前有一圈整数（一共n个），你要按顺序将其分为m个部分，各部分内的数字相加，相加所得的m个结果对10取模后再相乘，最终得到一个数k。游戏的要求是使你所得的k最大或者最小。

例如，对于下面这圈数字（n=4,m=2）：

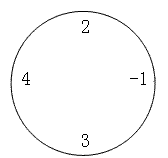
要求最小值时，((2−1)mod10)×((4+3)mod10)=1×7=7，要求最大值时，为((2+4+3)mod10)×(−1mod10)=9×9=81。特别值得注意的是，无论是负数还是正数，对10取模的结果均为非负值。

丁丁请你编写程序帮他赢得这个游戏。

输入格式

输入文件第一行有两个整数，n(1≤n≤50)和m(1≤m≤9)。以下n行每行有个整数，其绝对值 ≤\(10^4\)，按顺序给出圈中的数字，首尾相接。

输出格式

输出文件有2行，各包含1个非负整数。第1行是你程序得到的最小值，第2行是最大值。

输入输出样例

输入 #1 复制

4 2

4

3

-1

2

输出 #1 复制

7

81

分析

又是一道区间DP题

我们设\(f1[i][j][k]\)为将区间\([i,j]\)划分为\(k\)段的最小花费

那么就有\(f1[i][j][k]=min(f1[i][j][k],f1[i][c][k-1]*f1[c+1][j][1]);\)

其中尤其要注意\(k\)的范围\([2,min(m,d)]\),\(c\)的范围\([i+k-2,j)\)

如果范围错的话会出现爆\(long long\)的情况

\(f2\)最大花费的求法和\(f1\)完全相同

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=115;
ll f1[maxn][maxn][15],f2[maxn][maxn][15];
ll sum[maxn],a[maxn];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
        a[n+i]=a[i];
    }
    for(int i=1;i<=n*2;i++){
        sum[i]=sum[i-1]+a[i];
    }
    memset(f1,0x3f,sizeof(f1));
    for(int i=1;i<=n*2;i++){
    	for(int j=1;j<=n*2;j++){
    		f1[i][j][1]=((sum[j]-sum[i-1])%10+10)%10;
    		f2[i][j][1]=((sum[j]-sum[i-1])%10+10)%10;
    	}
    }
    for(int d=1;d<=n;d++){
        for(int i=1;i<=2*n-d+1;i++){
            int j=i+d-1;
            for(int k=2;k<=min(m,d);k++){
                for(int c=i+k-2;c<j;c++){
                    f1[i][j][k]=min(f1[i][j][k],f1[i][c][k-1]*f1[c+1][j][1]);
                    f2[i][j][k]=max(f2[i][j][k],f2[i][c][k-1]*f2[c+1][j][1]);
                }
            }
        }
    }
    ll ans=0x3f3f3f3f3f3f3f3f;
    ll ans1=-0x3f3f3f3f3f3f3f3f;
    for(int i=1;i<=n;i++){
        ans=min(ans,f1[i][i+n-1][m]);
        ans1=max(ans1,f2[i][i+n-1][m]);
    }
    printf("%lld\n%lld\n",ans,ans1);
    return 0;
}