Bellman-Ford算法例题：P3371 单源最短路径

看到还没人用Bellman-Ford过，赶紧水一发

lz非常弱，求各位大佬轻喷qwq

洛谷题目传送门：P3371

0.“松弛”操作

如果存在一条边$(u,v)$通过中继的方式可以让起点到$v$的距离缩短，那么就通过中继点缩短这个距离。

举个栗子：

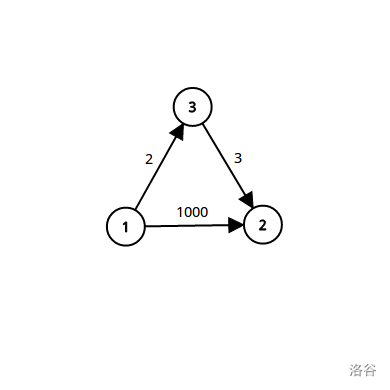
(用数组$dis[]$来表示起点到每个点的距离，以下同样)

一开始，$dis[2]=1000$，$dis[3]=2$（默认起点为1,以下同样）

通过3中继明显比从1直接到2要短，于是我们把$dis[2]$更新为$dis[3]+3=5$（从起点到3再到5）

于是你理解了什么是松弛

1.Bellman-Ford

Bellman-Ford的思想是用每条边进行松弛，每条边松弛$n-1$次，就一定能求出起点到每个点的距离

（如果你能感性理解你就不用看下面了）

为什么？因为每松弛1轮（我们管用每条边都松弛一次叫一轮），最短路就至少“生长”1个点。

再举个例子：

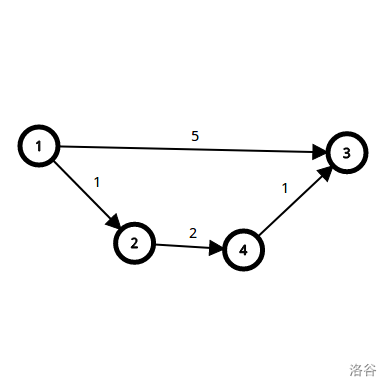
这是个很美丽的有向图。

最开始，除了$dis[1]$之外，其他所有$dis$都是无穷大。（到不了距离不就是无穷大嘛）。

第1轮松弛：

$dis[1]=0$（自己到自己距离肯定是0）

$dis[2]=min(dis[2],dis[1]+1)=min(INF,1)=1$

$dis[3]=min(dis[3],dis[1]+5)=min(INF,1)=1$

（由于边的顺序问题，松弛出来的结果可能不太一样）

（最坏情况可能只松弛1层）

（现在你明白“生长”是什么意思了吗）

第2轮松弛：

$dis[4]=min(dis[4],dis[2]+2)=min(INF,3)=3$

第3轮松弛：

$dis[3]=min(dis[3],dis[4]+1)=min(5,4)=4$

正好松弛了$n-1$轮。

因为，一个图最多有$n-1$层：例如，$1->2->3->...->n$，这个图（最坏情况）就正好要松弛$n-1$轮。

于是你理解了Bellman-Ford。

Code:

#include <bits/stdc++.h>

using namespace std;

#define MAXN 500005

#define INF 0x7fffffff

struct edge{

    int u,v,w;

    edge(){u=v=w=0;}

};

edge g[MAXN],cnt;

int n,m,s,dis[MAXN];

int main(){

    scanf("%d%d%d",&n,&m,&s);

    for(int i=1;i<=m;i++){

        int u,v,w;

        scanf("%d%d%d",&u,&v,&w);

        g[i].u=u;

        g[i].v=v;

        g[i].w=w;//存边

    }

    fill(dis+1,dis+1+n,INF);

    dis[s]=0;

    for(int i=1;i<=n-1;i++){//松弛n-1轮

        for(int j=1;j<=m;j++){

            int u=g[j].u,v=g[j].v,w=g[j].w;

            if(dis[u]==INF){continue;}//如果当前边的起点到不了那就没法松弛

            if(dis[v]>dis[u]+w){

                dis[v]=dis[u]+w;

            }

        }

    }

    for(int i=1;i<=n;i++){

        printf("%d ",dis[i]);

    }

    printf("\n");

    return 0;

}

一交，70pts，所以还要优化。

3.优化

但是，很多情况根本不用松弛$n-1$轮。

如果松弛到中间一轮松弛不动了（也就是$dis$不变了），那么以后再怎么松弛也不会变（因为已经求出最优解了），为什么可以思考一下。（其实就是我懒得写了233）

AC Code:

#include <bits/stdc++.h>

using namespace std;

#define MAXN 500005

#define INF 0x7fffffff

struct edge{

   int u,v,w;

   edge(){u=v=w=0;}

};

edge g[MAXN],cnt;

int n,m,s,dis[MAXN];

int main(){

   scanf("%d%d%d",&n,&m,&s);

   for(int i=1;i<=m;i++){

       int u,v,w;

       scanf("%d%d%d",&u,&v,&w);

       g[i].u=u;

       g[i].v=v;

       g[i].w=w;

   }

   fill(dis+1,dis+1+n,INF);

   dis[s]=0;

   for(int i=1;i<=n-1;i++){

       bool flag=true;

       for(int j=1;j<=m;j++){

           int u=g[j].u,v=g[j].v,w=g[j].w;

           if(dis[u]==INF){continue;}

           if(dis[v]>dis[u]+w){

               dis[v]=dis[u]+w;

               flag=false;

           }

       }

       if(flag){

           break;//如果没有松弛过那就没必要再松弛了

       }

   }

   for(int i=1;i<=n;i++){

       printf("%d ",dis[i]);

   }

   printf("\n");

   return 0;

}

4.时间复杂度

最坏情况$O(nm)$，最好情况$O(m)$（但是只有RP爆表的情况下才会达到），非常离谱。如果不是因为数据水人品好玄学原因，几乎一定会TLE。

还有一种Bellman-Ford优化，叫SPFA已死。所以，我建议在座的各位dalao先学Bellman-Ford再学SPFA

SPFA的最坏情况$O(nm)$，最好情况$O(m)$，但是除非故意卡（非常容易被卡！），一般都是$O(m)$

SPFA留着以后再讲吧，LZ要去吃饭了。