BZOJ2194:快速傅立叶之二(FFT)

Description

请计算C[k]=sigma(a[i]*b[i-k]) 其中 k < = i < n ，并且有 n < = 10 ^ 5。 a,b中的元素均为小于等于100的非负整数。

Input

第一行一个整数N,接下来N行，第i+2..i+N-1行，每行两个数，依次表示a[i],b[i] (0 < = i < N)。

Output

输出N行，每行一个整数，第i行输出C[i-1]。

Sample Input

5
3 1
2 4
1 1
2 4
1 4

Sample Output

24
12
10
6
1

Solution

QvQ我FFT也就能打个板子了

对FFT的运用还是不够到位，理解也只是仅仅停留在表面的地方

很多细节处以及证明并没有非常理解

啥时候数学底子够了再回来重新补FFT的证明什么奇奇怪怪的东西吧

反正学长告诉我我会打板子会用就好了

 

首先做这个题之前我还不知道FFT式子的基本形式（逃

 

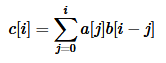
像这样下标和一定的式子就能用FFT进行优化了

下方公式转自https://blog.csdn.net/ycdfhhc/article/details/50636751

因为我不会markdown

一开始我们发现初始式子并不是FFT的形式没法搞

然后我们就将B数组翻转过来，然后发现下标和一定了……

然后把式子用另一个D表示出来，然后就可以FFT了……

答案C(0~n-1)对应D(n-1,n+n-2)

快二轮了感觉没啥希望

Code

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #define N (400000+100)
 using namespace std;

 double pi=acos(-1.0);
 int n,fn,l,r[N];
 struct complex
 {
     double x,y;
     complex (double xx=,double yy=)
     {
         x=xx; y=yy;
     }
 }a[N],b[N];

 complex operator + (complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
 complex operator - (complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
 complex operator * (complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
 complex operator / (complex a,double b){return complex(a.x/b,a.y/b);}

 void FFT(int n,complex *a,int opt)
 {
     for (int i=; i<n; ++i)
         if (i<r[i])
             swap(a[i],a[r[i]]);
     for (int k=; k<n; k<<=)
     {
         complex wn=complex(cos(pi/k),opt*sin(pi/k));
         for (int i=; i<n; i+=(k<<))
         {
             complex w=complex(,);
             for (int j=; j<k; ++j,w=w*wn)
             {
                 complex x=a[i+j], y=w*a[i+j+k];
                 a[i+j]=x+y; a[i+j+k]=x-y;
             }
         }
     }
     if (opt==-) for (int i=; i<n; ++i) a[i]=a[i]/n;
 }

 int main()
 {
     scanf("%d",&n); n--;
     for (int i=; i<=n; ++i)
         scanf("%lf%lf",&a[i].x,&b[n-i].x);
     fn=;
     while (fn<=n+n) fn<<=, l++;
     for (int i=; i<fn; ++i)
         r[i]=(r[i>>]>>) | ((i&)<<(l-));
     FFT(fn,a,); FFT(fn,b,);
     for (int i=; i<=fn; ++i)
         a[i]=a[i]*b[i];
     FFT(fn,a,-);
     for (int i=n; i<=n+n; ++i)
         printf("%d\n",(int)(a[i].x+0.5));
 }