数据结构（二） --- 伸展树（Splay Tree）

文章图片和代码来自邓俊辉老师课件

概述

伸展树（Splay Tree），也叫分裂树，是一种二叉排序树，它能在O(log n)内完成插入、查找和删除操作。它由丹尼尔·斯立特Daniel Sleator 和 罗伯特·恩卓·塔扬Robert Endre Tarjan 在1985年发明的。（出处百度百科）

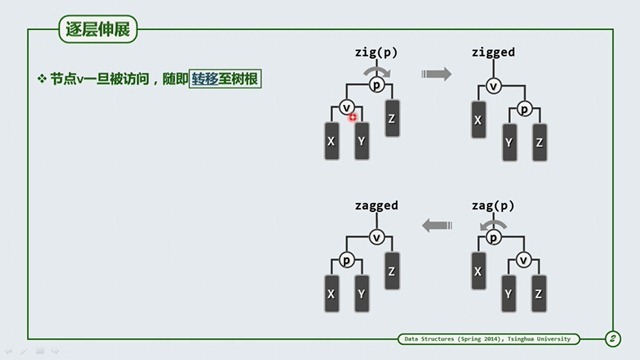
它的操作就是将访问到的元素放在根节点处。主要的操作就是 zip 和 zag

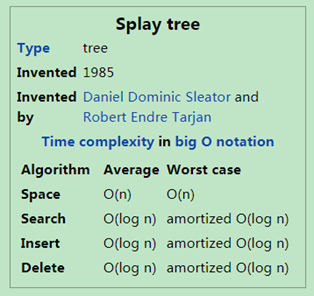
下面是空间/时间复杂度（出处）

算法分析

双层伸展

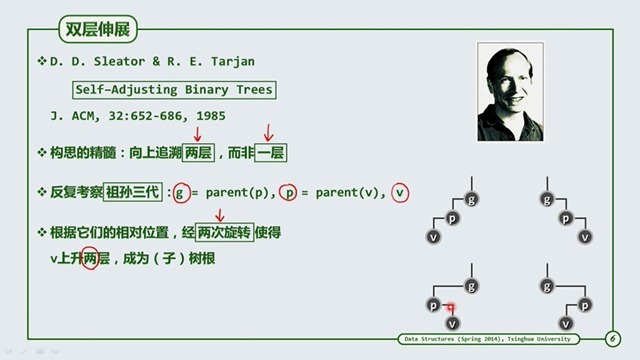
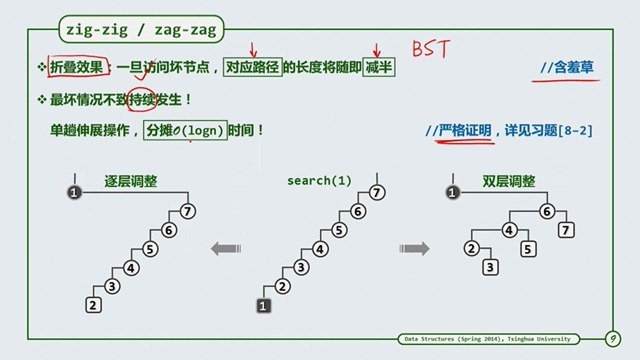
双层伸展的作用是提升了树平均的访问性能。构思的精髓 ： 向上追溯两层，而非一层。 右下角是伸展树需要处理的四种情况。具体的处理是怎么样的呢？

双层伸展主要在 zig-zip 和 zag-zag 的情况下发挥作用，例如要使v 升到根节点，双层伸展要求我们使用先对祖父节点zig，然后再做一次zip ，即是下部分三幅图演示的那样。下面我们看一下使用这种方法真的可以提升性能吗。

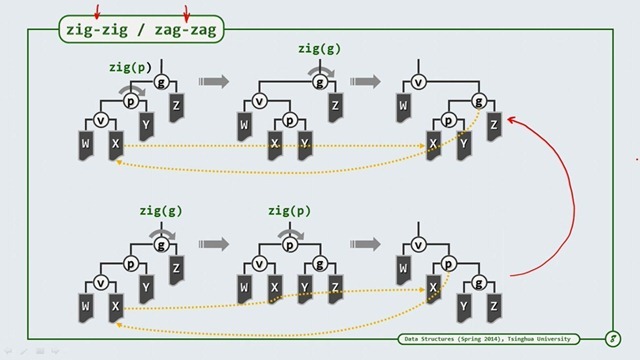
分摊性能

我们可以看到左边是逐层调整的方法，而右边是双层调整的方法，右边的子树的高度很明显比左边的矮了一半，当下一次又遇到最坏节点时，由于高度矮了一半了，那么性能自然就提升了。所以平均分摊时间可以达到 logn .

算法实现

代码是根绝邓老师的提供的代码用java改写的，添加了部分注释

主要处理的四种情况可以详见下面的代码

  1 package Splay;
  2
  3
  4 public class Node {
  5     Node left;
  6     Node right;
  7     Node parent;
  8     int value;
  9
 10     public Node(int value) {
 11         this.value = value;
 12     }
 13
 14     public boolean isLeftChild() {
 15         return parent != null && (parent.left == this);
 16         //根节点，我们直接返回false
 17     }
 18
 19     public boolean isRightChild() {
 20         return parent != null && (parent.right == this);
 21         //根节点，我们直接返回false
 22     }
 23
 24     @Override
 25     public String toString() {
 26         return "该节点的值为：" + value + " 左节点：" + ((left!=null)? left.value:"无") + " 右节点：" + ((right!=null)? right.value:"无") + " 父节点：" + ((parent!=null)? parent.value:"无");
 27     }
 28 }
 29 

  1 package Splay;
  2
  3
  4 import com.sun.org.apache.bcel.internal.generic.IF_ACMPEQ;
  5
  6 import javax.management.modelmbean.ModelMBean;
  7
  8 /**
  9  * Splay Tree (伸展树)
 10  *
 11  *
 12  */
 13 public class SplayTree {
 14
 15     public Node root;
 16
 17     /**
 18      * @param val 插入节点的值
 19      */
 20     public Node insert(int val) throws Exception {
 21         if (root == null) {
 22             root = new Node(val);
 23             return null;
 24         }
 25         Node node = search(val);
 26         //search操作查找是否存在该节点
 27         if (node.value == val) {
 28             return node;
 29         } else { //search操作找不到该节点,查找返回的是hot节点，插入的节点再和hot重新装配
 30             Node newRoot = new Node(val);
 31             if (val > node.value) {
 32                 node.parent = newRoot;
 33                 newRoot.left = node;
 34                 newRoot.right = node.right;
 35                 if (node.right != null) {
 36                     node.right.parent = newRoot;
 37                     node.right = null;
 38                 }
 39             } else {
 40                 node.parent = newRoot;
 41                 newRoot.right = node;
 42                 newRoot.left = node.left;
 43                 if (node.left != null) {
 44                     node.left.parent = newRoot;
 45                     node.left = null;
 46                 }
 47             }
 48             root = newRoot;
 49             return newRoot;
 50         }
 51     }
 52
 53     /**
 54      * 删除某个节点
 55      * @param val 删除的节点
 56      * @return true 成功删除，反之
 57      */
 58     public boolean delete(int val)throws Exception{
 59        Node node =  search(val);
 60         if (node.value == val) {  //找到该节点
 61             if (node.left == null) { //没有左子树
 62                 root = node.right;
 63                 node.right.parent = null;
 64                 node.right = null;
 65             } else if (node.right == null) { //没有右子树
 66                 root = node.left;
 67                 node.left.parent = null;
 68                 node.left = null;
 69             }else { //节点存在左右子树
 70                 //暂时切除左子树，然后右子树中最小的节点，在连接起来
 71                 Node lTree = node.left;
 72                 lTree.parent = null;
 73                 root.left = null;
 74                 search(node.value);
 75                 //最小的节点必然上升到了根节点,此时的root应该是右子树中最小的节点
 76                 root.left = lTree;
 77                 lTree.parent = root;
 78                 node = null; //原来的节点置null
 79             }
 80             return true;
 81         }else {
 82             return false;
 83         }
 84     }
 85
 86     /**
 87      * 计算整个树的高度
 88      *
 89      * @return
 90      */
 91     public int height() {
 92         Node node;
 93         int lh = 1, rh = 1;
 94         node = root.left;
 95         while (node != null) {
 96             lh++;
 97             node = node.left;
 98         }
 99
100         node = root.right;
101         while (node != null) {
102             rh++;
103             node = node.right;
104         }
105
106         return Math.max(lh, rh);
107     }
108
109     /**
110      *  中序递归打印
111      * @param node
112      */
113     public void printMidNum(Node node) {
114         if (node != null) {
115             printMidNum(node.left);
116             System.out.print(node.value + " ");
117 //            System.out.println(node.toString());
118             printMidNum(node.right);
119         }
120     }
121
122
123     /**
124      * @param value 使用伸展策略搜寻的某个值，
125      * @return 返回查找到的node, 树中没有该元素返回null
126      */
127     public Node search(int value) throws Exception {
128         /*
129           搜索某个节点是不是存在，调用splay方法
130          */
131         Node compare;
132         Node target; //目标节点
133         Node hot = null; //目标附近节点
134         compare = root;
135
136         if (compare == null) {
137             throw new Exception("该树为空树");
138         }
139         //查找某个节点
140         while (true) {
141             if (compare == null) {
142                 target = null;
143                 break;
144             } else if (compare.value == value) {
145                 target = compare;
146                 break;
147             }
148             if (compare.value > value) {
149                 hot = compare;
150                 compare = compare.left;
151             } else {
152                 hot = compare;
153                 compare = compare.right;
154             }
155         }
156
157         if (target == null) {
158             root = splay(hot);
159             return null;
160         }
161
162         return (root = splay(target));
163     }
164
165
166     public void attachAsLChild(Node parent, Node lChild) {
167         parent.left = lChild;
168         if (lChild != null)
169             lChild.parent = parent;
170     }
171
172     void attachAsRChild(Node parent, Node rChild) {
173         parent.right = rChild;
174         if (rChild != null)
175             rChild.parent = parent;
176     }
177
178     /**
179      * 传入的 v 必须存在于树中，由调用的方法保证
180      * splay 方法针对情况进行转换，转换的思路是重新对各个节点的位置装配，装配的意思指的是
181      * 根据初始的位置和最终的位置拆解-重连的操作
182      *
183      * @param v v为因最近访问而需伸展的节点位置
184      * @return 调整之后新树根应为被伸展的节点，故返回该节点的位置以便上层函数更新树根
185      */
186     public Node splay(Node v) {
187         if (v == null) return null;
188         //*v的父亲与祖父
189         Node p;
190         Node g;
191         while ((p = v.parent) != null && (g = p.parent) != null) { //自下而上，反复对*v做双层伸展
192             Node gg = g.parent; //每轮之后*v都以原曾祖父（great-grand parent）为父
193             if (v.isLeftChild()) {
194                 if (p.isLeftChild()) { //zig-zig
195                     attachAsLChild(g, p.right);
196                     attachAsLChild(p, v.right);
197                     attachAsRChild(p, g);
198                     attachAsRChild(v, p);
199                 } else { //zig-zag
200                     attachAsLChild(p, v.right);
201                     attachAsRChild(g, v.left);
202                     attachAsLChild(v, g);
203                     attachAsRChild(v, p);
204                 }
205             } else if (p.isRightChild()) { //zag-zag
206                 attachAsRChild(g, p.left);
207                 attachAsRChild(p, v.left);
208                 attachAsLChild(p, g);
209                 attachAsLChild(v, p);
210             } else { //zag-zig
211                 attachAsRChild(p, v.left);
212                 attachAsLChild(g, v.right);
213                 attachAsRChild(v, g);
214                 attachAsLChild(v, p);
215             }
216
217             //重连子树，并判断是否loop是否结束
218             if (gg == null)
219                 v.parent = null; //若*v原先的曾祖父*gg不存在，则*v现在应为树根
220             else //否则，*gg此后应该以*v作为左或右孩子
221                 if (g == gg.left) {
222                     attachAsLChild(gg, v);
223                 } else {
224                     attachAsRChild(gg, v);
225                 }
226
227         }
228         //双层伸展结束时，必有g == NULL，但p可能非空,即是目标到根节点之间还有一个节点，需要一次单旋解决
229         if ((p = v.parent) != null) {
230             if (v.isLeftChild()) {
231                 attachAsLChild(p, v.right);
232                 attachAsRChild(v, p);
233             } else {
234                 attachAsRChild(p, v.left);
235                 attachAsLChild(v, p);
236             }
237         }
238         v.parent = null;
239         return v;
240     }
241
242
243 }
244
245
246 

代码中的注释已经说明了各个操作的流程，需要注意的是insert 和 delete方法，由于这两个方法在实现的时候都会先调用search方法，我们使用了一个hot 节点，表示离目标节点最近的节点，让hot 节点上升到根节点，方便我们在insert和delete后续的使用。

综合评价

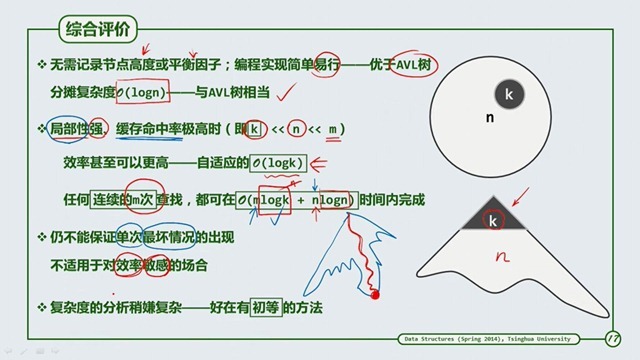
不能保证单次最坏情况的出现的原因是，假如我们一开始要找的那个点就在最底下，那么就可能达到了最坏的情况。

参考资料

• 邓俊辉老师的数据结构课程