NumPy - 线性代数

NumPy 包包含numpy.linalg模块，提供线性代数所需的所有功能。此模块中的一些重要功能如下表所述。

序号	函数及描述
1.	`dot` 两个数组的点积
2.	`vdot` 两个向量的点积
3.	`inner` 两个数组的内积
4.	`matmul` 两个数组的矩阵积
5.	`determinant` 数组的行列式
6.	`solve` 求解线性矩阵方程
7.	`inv` 寻找矩阵的乘法逆矩阵

`numpy.dot()`

此函数返回两个数组的点积。对于二维向量，其等效于矩阵乘法。对于一维数组，它是向量的内积。对于 N 维数组，它是a的最后一个轴上的和与b的倒数第二个轴的乘积。

import numpy.matlib

import numpy as np 

a = np.array([[1,2],[3,4]])

b = np.array([[11,12],[13,14]])

np.dot(a,b)

Python

输出如下：

[[37  40]

 [85  92]]

Python

要注意点积计算为：

[[1*11+2*13, 1*12+2*14],[3*11+4*13, 3*12+4*14]]

`numpy.vdot()`

此函数返回两个向量的点积。如果第一个参数是复数，那么它的共轭复数会用于计算。如果参数id是多维数组，它会被展开。

例子

import numpy as np

a = np.array([[1,2],[3,4]])

b = np.array([[11,12],[13,14]])

print np.vdot(a,b)

Python

输出如下：

Python

注意：1*11 + 2*12 + 3*13 + 4*14 = 130。

`numpy.inner()`

此函数返回一维数组的向量内积。对于更高的维度，它返回最后一个轴上的和的乘积。

例子

import numpy as np

print np.inner(np.array([1,2,3]),np.array([0,1,0]))

# 等价于 1*0+2*1+3*0

Python

输出如下：

Python

例子

# 多维数组示例

import numpy as np

a = np.array([[1,2], [3,4]]) 

print '数组 a：'

print a

b = np.array([[11, 12], [13, 14]]) 

print '数组 b：'

print b 

print '内积：'

print np.inner(a,b)

Python

输出如下：

数组 a：

[[1 2]

[3 4]]

数组 b：

[[11 12]

[13 14]]

内积：

[[35 41]

[81 95]]

Python

上面的例子中，内积计算如下：

1*11+2*12, 1*13+2*14

3*11+4*12, 3*13+4*14

Python

`numpy.matmul`

numpy.matmul()函数返回两个数组的矩阵乘积。虽然它返回二维数组的正常乘积，但如果任一参数的维数大于2，则将其视为存在于最后两个索引的矩阵的栈，并进行相应广播。

另一方面，如果任一参数是一维数组，则通过在其维度上附加 1 来将其提升为矩阵，并在乘法之后被去除。

例子

# 对于二维数组，它就是矩阵乘法

import numpy.matlib

import numpy as np 

a = [[1,0],[0,1]]

b = [[4,1],[2,2]]

print np.matmul(a,b)

Python

输出如下：

[[4  1]

 [2  2]]

Python

例子

# 二维和一维运算

import numpy.matlib

import numpy as np 

a = [[1,0],[0,1]]

b = [1,2]

print np.matmul(a,b)

print np.matmul(b,a)

Python

输出如下：

[1  2]

[1  2]

Python

例子

# 维度大于二的数组

import numpy.matlib

import numpy as np 

a = np.arange(8).reshape(2,2,2)

b = np.arange(4).reshape(2,2)

print np.matmul(a,b)

Python

输出如下：

[[[2   3]

   [6   11]]

  [[10  19]

   [14  27]]]

Python

`numpy.linalg.det()`

行列式在线性代数中是非常有用的值。它从方阵的对角元素计算。对于 2×2 矩阵，它是左上和右下元素的乘积与其他两个的乘积的差。

换句话说，对于矩阵[[a，b]，[c，d]]，行列式计算为ad-bc。较大的方阵被认为是 2×2 矩阵的组合。

numpy.linalg.det()函数计算输入矩阵的行列式。

例子

import numpy as np

a = np.array([[1,2], [3,4]])

print np.linalg.det(a)

Python

输出如下：

-2.0

Python

例子

b = np.array([[6,1,1], [4, -2, 5], [2,8,7]])

print b

print np.linalg.det(b)

print 6*(-2*7 - 5*8) - 1*(4*7 - 5*2) + 1*(4*8 - -2*2)

Python

输出如下：

[[ 6 1 1]

 [ 4 -2 5]

 [ 2 8 7]]

-306.0

-306

Python

`numpy.linalg.solve()`

numpy.linalg.solve()函数给出了矩阵形式的线性方程的解。

考虑以下线性方程：

x + y + z = 6

2y + 5z = -4

2x + 5y - z = 27

Python

可以使用矩阵表示为：

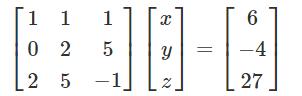
如果矩阵成为A、X和B，方程变为：

AX = B

Python

或

X = A^(-1)B

Python

`numpy.linalg.inv()`

我们使用numpy.linalg.inv()函数来计算矩阵的逆。矩阵的逆是这样的，如果它乘以原始矩阵，则得到单位矩阵。

例子

import numpy as np 

x = np.array([[1,2],[3,4]])

y = np.linalg.inv(x)

print x

print y

print np.dot(x,y)

Python

输出如下：

[[1 2]

 [3 4]]

[[-2.   1. ]

 [ 1.5 -0.5]]

[[  1.00000000e+00   1.11022302e-16]

 [  0.00000000e+00   1.00000000e+00]]

Python

例子

现在让我们在示例中创建一个矩阵A的逆。

import numpy as np

a = np.array([[1,1,1],[0,2,5],[2,5,-1]]) 

print '数组 a：'

print a

ainv = np.linalg.inv(a) 

print 'a 的逆：'

print ainv  

print '矩阵 b：'

b = np.array([[6],[-4],[27]])

print b 

print '计算：A^(-1)B：'

x = np.linalg.solve(a,b)

print x

# 这就是线性方向 x = 5, y = 3, z = -2 的解

Python

输出如下：

数组 a：

[[ 1 1 1]

 [ 0 2 5]

 [ 2 5 -1]]

a 的逆：

[[ 1.28571429 -0.28571429 -0.14285714]

 [-0.47619048 0.14285714 0.23809524]

 [ 0.19047619 0.14285714 -0.0952381 ]]

矩阵 b：

[[ 6]

 [-4]

 [27]]

计算：A^(-1)B：

[[ 5.]

 [ 3.]

 [-2.]]

Python

结果也可以使用下列函数获取

x = np.dot(ainv,b)