重新整理数据结构与算法(c#)—— 算法套路动态规划算法[二十六]

前言

动态规划算法的核心思想是:将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法。

这样一听和分治算法有点相似啊。

是的，分治算法也是将大问题分为小问题，但是他们毕竟不同，不同之处在什么地方呢?

分治算法是这样的，本来有一个大问题，把他们呢分成10个独立的小问题，每个问题都可以单独执行。

而动态规划是这样子的，他一个问题分为10个小问题，解决一个问题需要上一个问题得出的结论，在原先问题解决得基础上得到答案。

这个问题该怎么求呢？

比如我们看电视有很多个频道，我们会经常换台，如果频道多了，那么这时候选择多就出现难选择得问题了。

现在给我4Kg背包，如果给我1kg那么该怎么选呢？现在1kg给我

看下图:

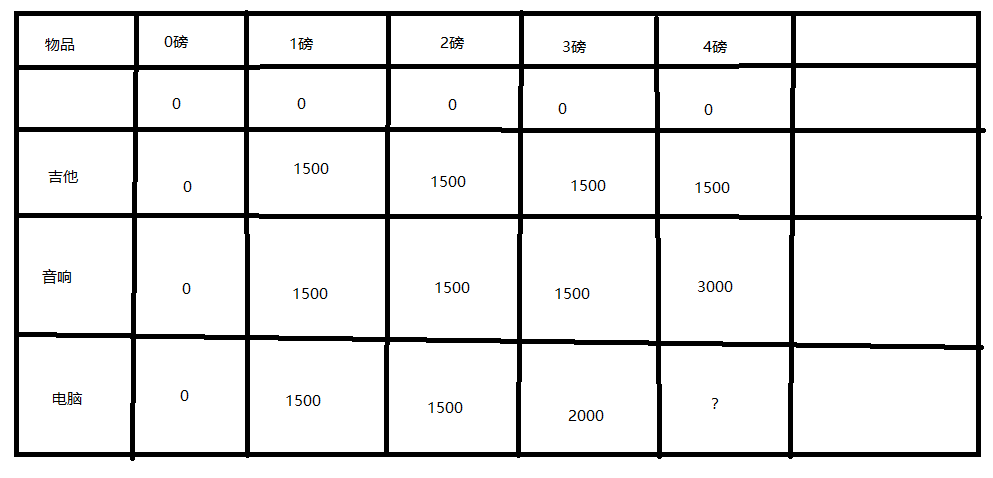
上面这个表格得意思是这样得，比如x轴1磅y轴吉他，这个1500的意思是假如背包只能装1kg，只能选吉他，那么背包价格为1500。

x轴1磅y轴音响的时候，这个1500的意思是假如背包只能装1kg，只能选吉他和音响，那么背包价格为1500。其他类推。

那么这些数据对这个4磅3个都可以选有什么用？

看红色这一块:

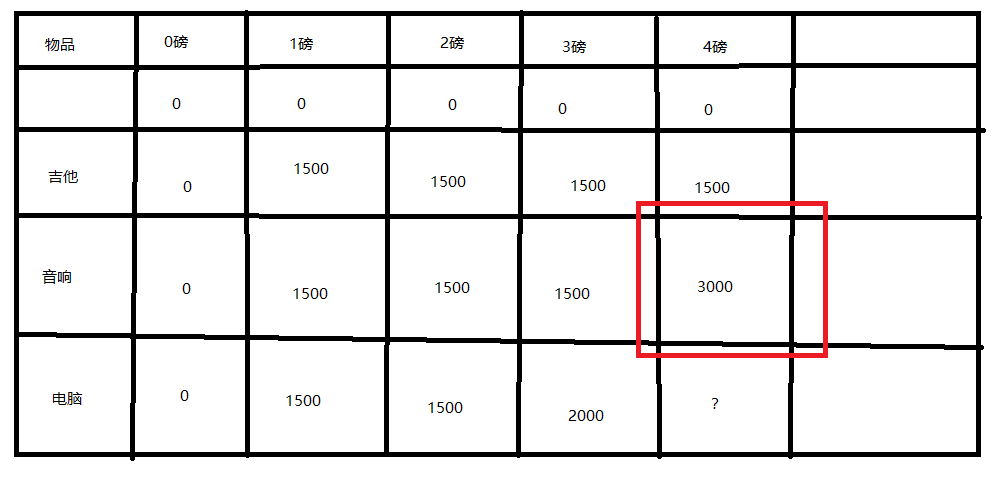
这个数据有什么用呢？假设我们4磅都装不下新增可以装的物品电脑，那么可想而知，其实结果就是3000。

为什么这么判断呢？假设装不下电脑，那么可以装的物品数量没变，而且背包大小没变，那么条件没有任何改变自然结果不变。

这时候分析：

1.假如4磅的时候装了3000的音响，那么这时候加入这个可以选电脑条件，那么是没有任何效果，还是3000。

2.假如3磅的时候装了一个电脑，那么多出的一磅该怎么选才最好呢？多出的一磅看下现在条件是啥？

现在的条件是背包1磅，有两个物品可以选这时候可以查表啊，如下图:

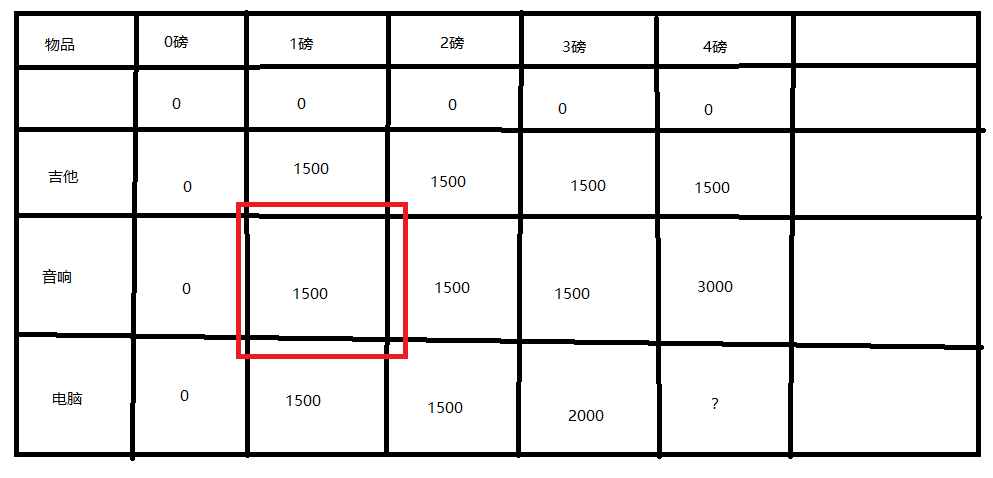
因为我们前面已经求出了背包1磅，有两个物品可以选的最优解。

这时候就得出最优解。

正文

代码如下:

int[] weight = {1,4,3 };
int[] val = {1500,3000,2000};
int m = 4;
int n = val.Length;
int[,] wv = new int[n+1,m+1];
//由于wv默认创建数组为0所以不必初始化第一行第一列为0
for (int i = 1; i <n+1; i++)
{
	for (int j = 1; j < m + 1; j++)
	{
		//如果现在背包的质量装不下新增物品的质量
		if (weight[i - 1] > j)
		{
			wv[i, j] = wv[i - 1, j];
		}
		else
		{
			//如果可以装下新增的商品,则尝试新增商品，取最大值
			wv[i, j] = Math.Max(wv[i-1,j],val[i-1]+wv[i-1,j-weight[i-1]]);
		}
	}
}
Console.WriteLine(wv[n,m]);
Console.Read();

结果为:

如果要记录加入了什么物品，可以这样。

代码如下:

static void Main(string[] args)
{
	//hanoiTower(5,'A','B','C');
	int[] weight = {1,4,3 };
	int[] val = {1500,3000,2000};
	string[] names = {"吉他","音响","电脑" };
	int m = 4;
	int n = val.Length;
	int[,] wv = new int[n+1,m+1];
	int[,] path = new int[n+1,m+1];
	//由于wv默认创建数组为0所以不必初始化第一行第一列为0
	for (int i = 1; i <n+1; i++)
	{
		for (int j = 1; j < m + 1; j++)
		{
			//如果现在背包的质量装不下新增物品的质量
			if (weight[i - 1] > j)
			{
				wv[i, j] = wv[i - 1, j];
			}
			else
			{
				//如果可以装下新增的商品,则尝试新增商品，取最大值
				if (val[i - 1] + wv[i - 1, j - weight[i - 1]] >= wv[i - 1, j])
				{
					wv[i, j] = val[i - 1] + wv[i - 1, j - weight[i - 1]];
					path[i, j] = 1;
				} else
				{
					wv[i, j] = wv[i - 1, j];
				}
			}
		}
	}
	Console.WriteLine(wv[n,m]);
	int a = n;
	int b = m;
	while (a > 0&&b>0)
	{
		if (path[a,b]==1)
		{
			Console.WriteLine("商品名字:"+names[a-1]+"重量:"+weight[a-1]+"价格:"+val[a-1]);
			b -= weight[a - 1];
		}
		a--;
	}
	Console.Read();
}

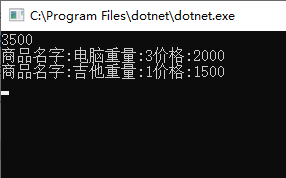
结果如下: