2021-05-27：定义何为step sum？比如680，680+68+6=754，680的step sum叫754。

2021-05-27：定义何为step sum？比如680，680+68+6=754，680的step sum叫754。给定一个整数num，判断它是不是某个数的step sum？

福大大 答案2021-05-27：

方法一：
自然智慧即可。二分法。在0到num之间找中点，然后求中点的step sum。如果step sum太大，取左边；如果step sum太小，取右边。时间复杂度是(log2N)*(log10N)。
方法二：
1.求出不大于num的最大的全1数，然后num/全1数。如果商大于等于10，直接返回false。
2.看余数。
2.1.当余数不为0时，num=余数，全1数=(全1数/10)，重复步骤1。
2.2.当余数为0时，返回true。
时间复杂度是log10N。

代码用golang编写。代码如下：

package main

import "fmt"

//05
func main() {
    count := 0
    for i := 1; i <= 11111; i++ {
        ret1 := isStepSum1(i)
        ret2 := isStepSum2(i)
        fmt.Println(i, ret1, ret2)
        count++
    }
    fmt.Println("正确数 = ", count)
}

//方法1
func isStepSum1(stepSum int) bool {
    L := 0
    R := stepSum
    M := 0
    cur := 0
    for L <= R {
        M = L + (R-L)>>1
        cur = getStepSum(M)
        if cur == stepSum {
            return true
        } else if cur < stepSum {
            L = M + 1
        } else {
            R = M - 1
        }
    }
    return false
}

func getStepSum(num int) int {
    sum := 0
    for num != 0 {
        sum += num
        num /= 10
    }
    return sum
}

//方法2
func isStepSum2(stepSum int) bool {
    global111 := getGlobal111(stepSum)
    for global111 > 0 {
        quotient := stepSum / global111  //商
        remainder := stepSum % global111 //余数
        if quotient >= 10 {
            return false
        }
        global111 /= 10
        stepSum = remainder
    }
    return true
}

func getGlobal111(num int) int {
    ans := 1
    anstemp := 11
    for anstemp <= num {
        ans = anstemp
        anstemp *= 10
        anstemp++
    }
    return ans
}

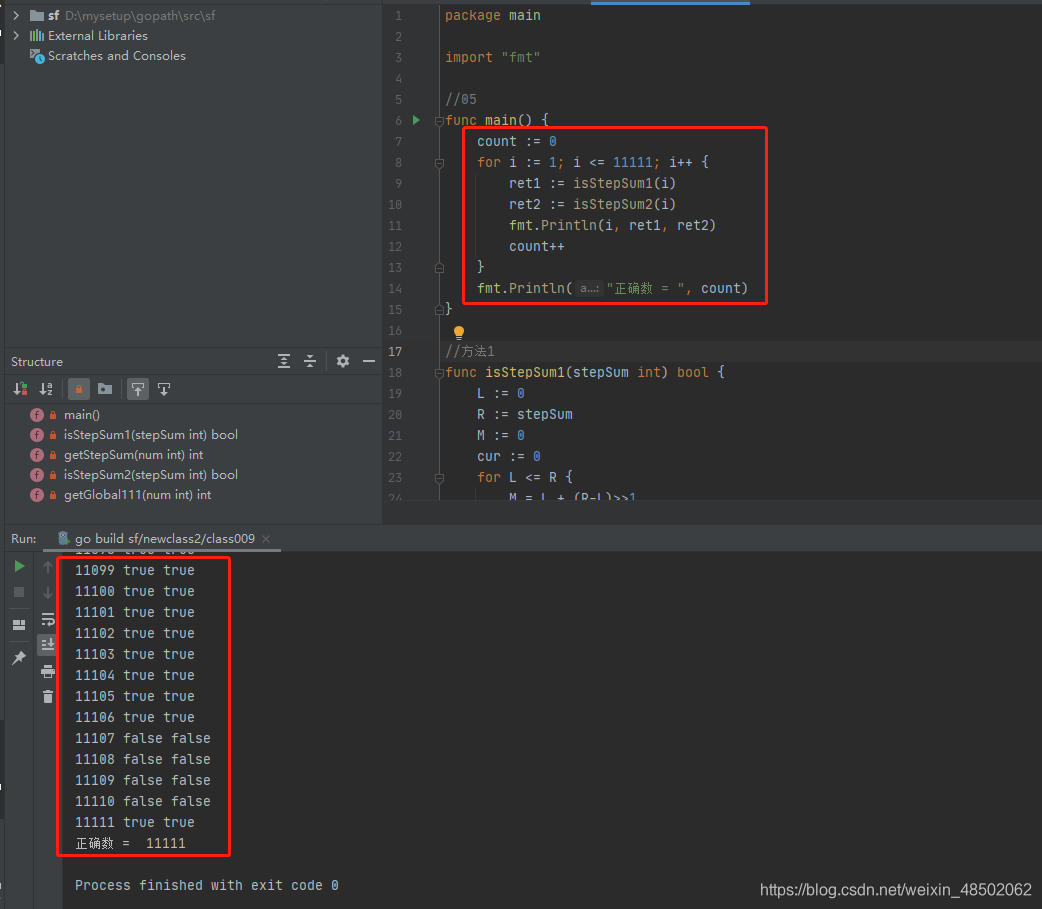
执行结果如下：

---

左神java代码