机器学习-决策树系列-GBDT算法-集成学习-30

目录

• 1. 复习
• 2. GBDT
• 3. gbdt应用于二分类：
• 3. gbdt应用于多类
• 4. 叶子节点输出值c的计算
• 5. GBDT的其他应用
• 6. GBDT+LR 代码实现

1. 复习

再开始学习GBDT算法之前 先复习一下之前的 线性回归 逻辑回归（二分类） 多分类

1. 线性回归
   
   找到一组W 使得 L 最小 进而求得F*
   
   

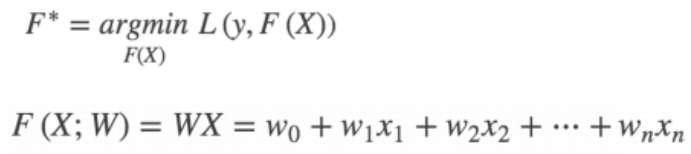
使用梯度下降法：

梯度下降的方向：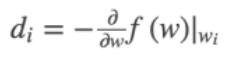

不断更新w: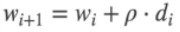

最终求得的w 可以表示为:

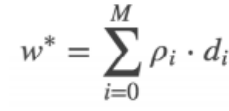
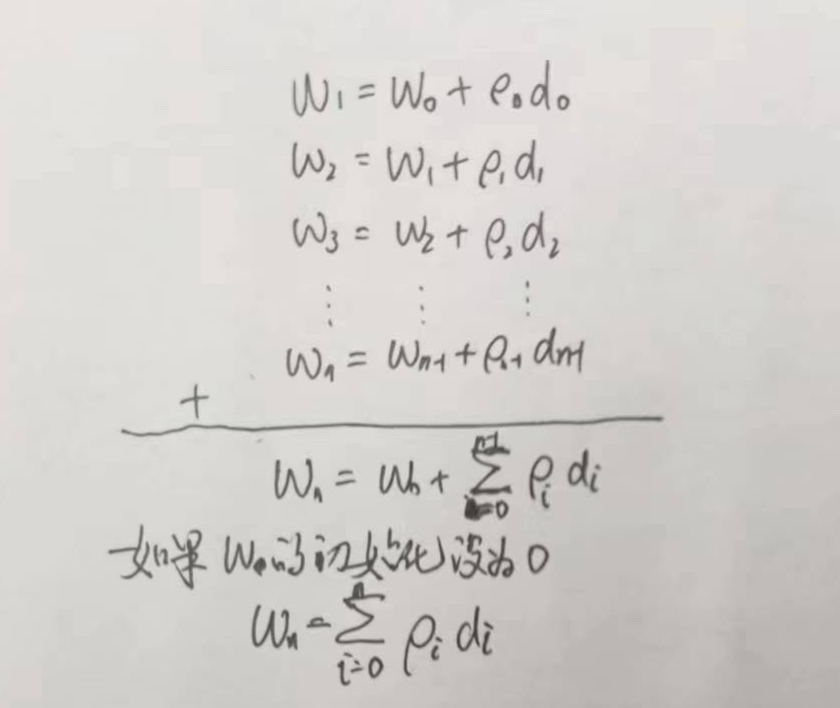
2.逻辑回归

逻辑回归 是 用于处理二分类的问题

只不过是将线性回归的输出 Wx结果 再用sigmoid函数 映射到 0-1 之间

sigmoid函数：

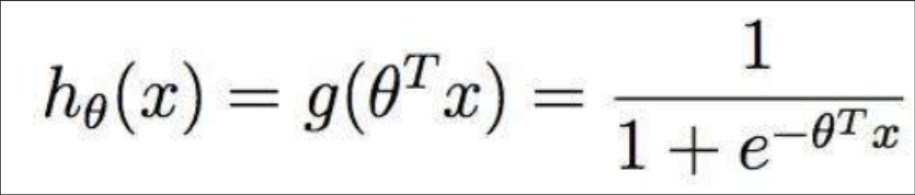
逻辑回归预测的结果是该样本为正例的概率

1. 多分类
   
   多分类：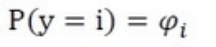

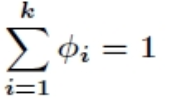
多分类求解的θ 跟线性回归的w不一样 而是一个矩阵



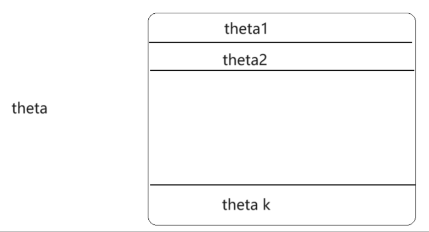
对于任意一条样本：

2. GBDT

gradient boost decision tree

初始化 第0棵 树 f0 （初始化的值 可以给0 为了快速拟合 给定一个先验概率 例如统计正例的比例）

计算残值 y-y_hat 训练第一棵树 f1

再计算残值 再训练 第二棵树 f2

...

直到满足收敛条件

模型做预测：sum(f1+f2+...+fm)

gbdt用于回归树

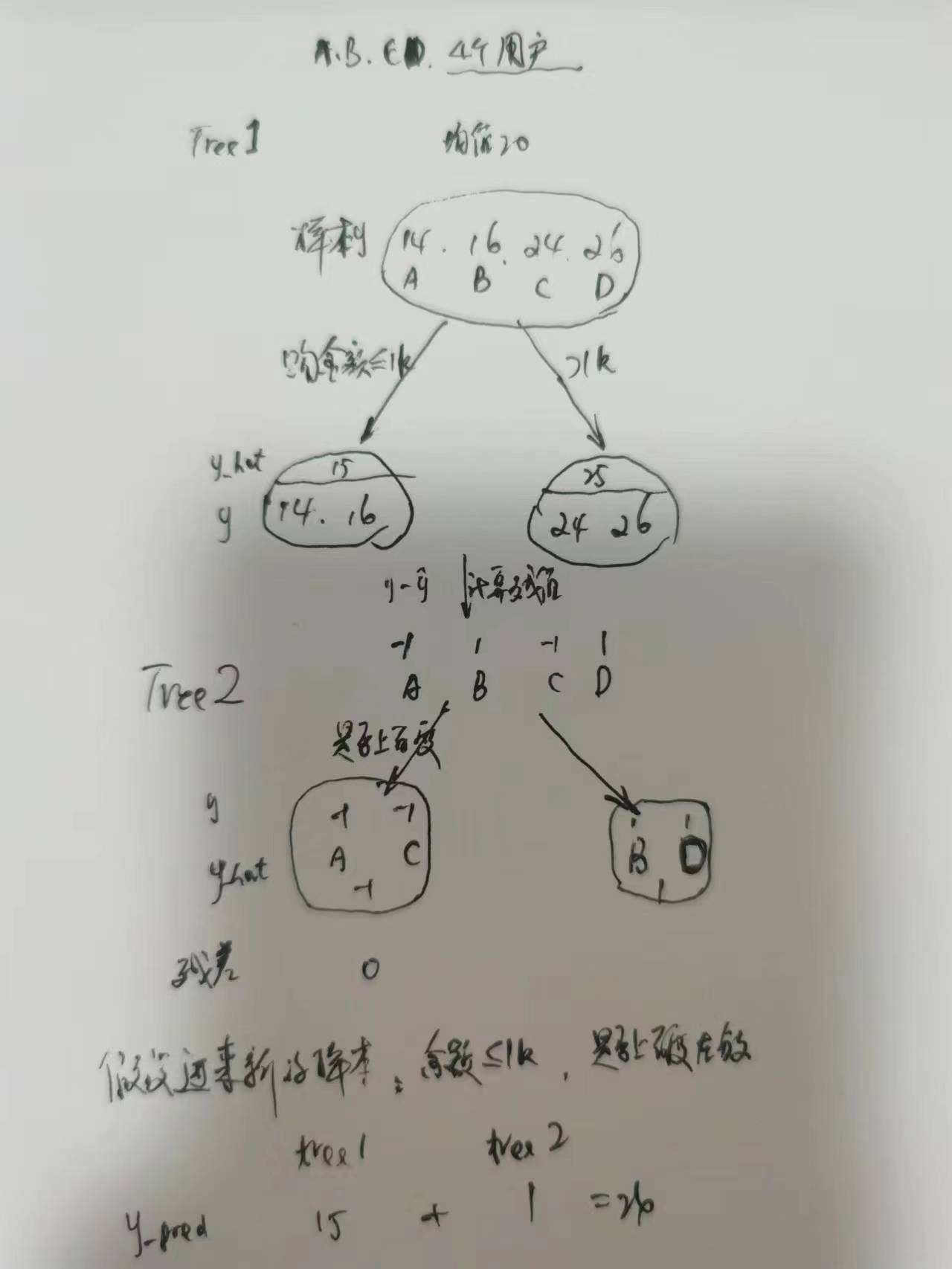
每一次计算都是为了减少上一次的残差。

AdaBoosting中关注正确错误的样本加权，也就是下一次会更重视上一次分错的。

3. gbdt应用于二分类：

之前学的逻辑回归，本质上是用一个线性模型去拟合对数几率：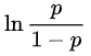

GBDT处理二分类也是一样，只是用一系列的梯度提升树去拟合这个对数几率。





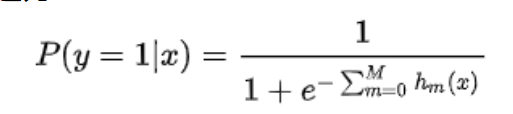
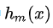
就是学习到的决策树

单条样本的熵：

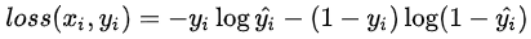
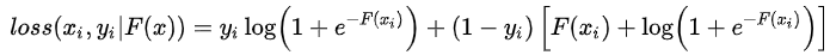
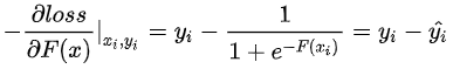
因此，与回归问题很类似，下一棵决策树的训练样本为：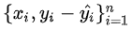

需要拟合的残差为真实标签与预测概率之差。

GBDT应用于二分类的算法：

1， 初始化：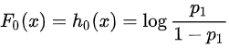

训练样本中y=1的比例，利用先验信息来初始化学习器

2. 训练的次数 for m=1, 2, 3, ...

3. 计算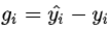

得到训练样本：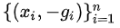



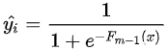
4. 得到学习器

3. gbdt应用于多类

多分类问题，则需要考虑以下softmax模型：



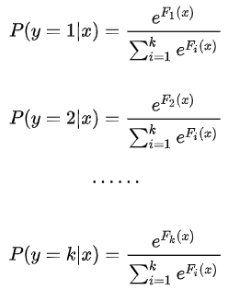
每一轮的训练实际上是训练了 k 棵树去拟合softmax的每一个分支模型的负梯度。

softmax模型的单样本损失函数为：

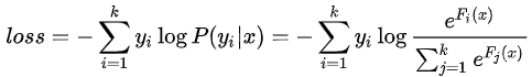
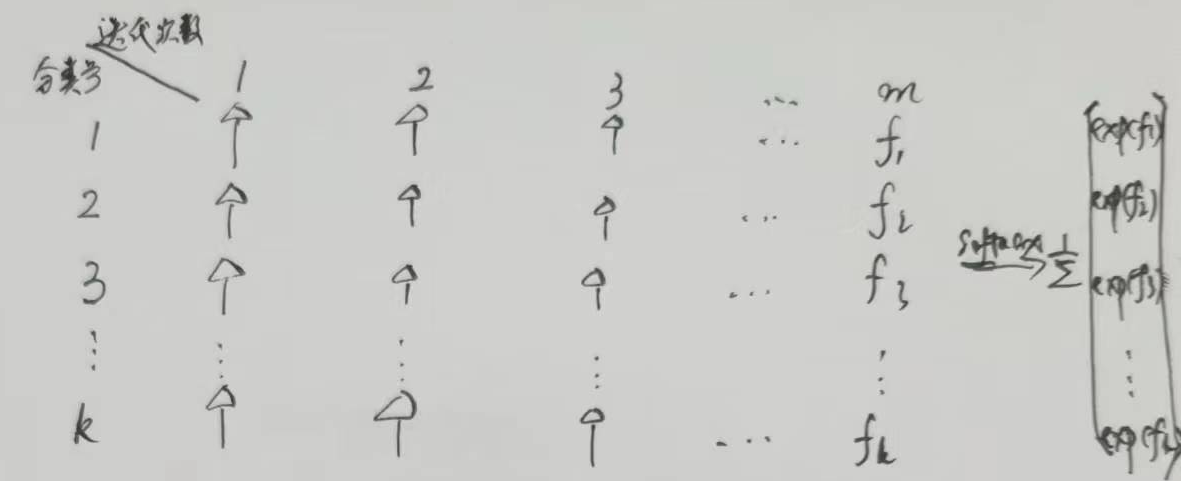
4. 叶子节点输出值c的计算

对于新生成的树，计算各个叶子节点的最佳残差拟合值c：



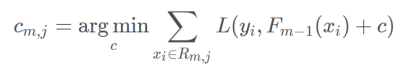
对于m次迭代， 所有落入j

推导过程：

GBDT算法：

1. init
2. -gradient
3. leaf node value update

5. GBDT的其他应用

1. 特征重要度
   
   树在做分叉的时候是根据某一特征值 来进行的
   
   特征j在单颗树中的重要度，是计算特征j在单颗树中带来的收益之和

例如：



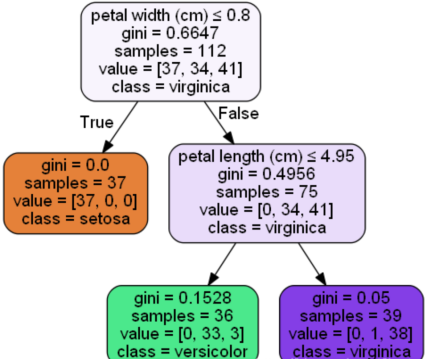
petal width (cm)就是根节点：feature importance=(112∗0.6647−75∗0.4956−37∗0)/112=0.5564007189

petal length (cm)的featureimportance=(75∗0.4956−39∗0.05−36∗0.1528)/112=0.4435992811

1. 特征组合对特征降维
   
   GBDT + LT
   
   

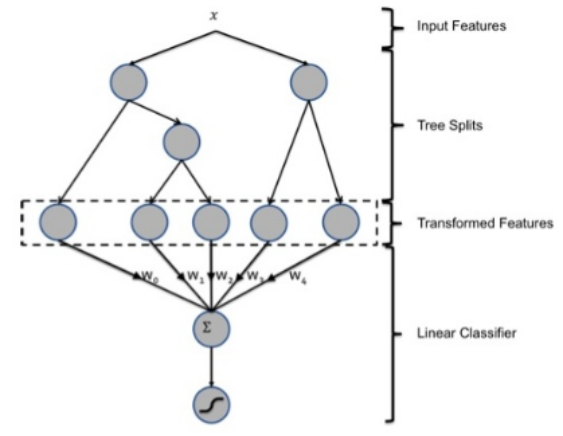
将X的特征（很多维度 几百个 甚至更多） 转化成GBDT输出的 几个组合特征

feature_1 feature_2, feature_3, feature_4, feature_5

x1 0 1 0 0 0

x2 1 0 0 0 0

...

再用这些新的特征去做一个LR 线性回归 给出预测值

6. GBDT+LR 代码实现

import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model._logistic import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
from sklearn.metrics._ranking import roc_auc_score

class GradientBoostingWithLr(object):
    def __init__(self):
        self.gbdt_model = None
        self.lr_model = None

        self.gbdt_encoder = None

        self.X_train_leafs = None
        self.X_test_leafs = None

        self.X_trans = None  # GBDT 转后之后的X

    def gbdt_train(self, X_train, y_train):
        """
        训练GBDT模型
        :return:
        """
        gbdt_model = GradientBoostingClassifier(
            n_estimators=10,
            max_depth=6,
            verbose=0,
            max_features=0.5  # 训练的时候 会计算那哪些特征 的收益 取最小 features are considered at each split.
        )
        gbdt_model.fit(X_train, y_train)
        return gbdt_model

    def lr_train(self, X_train, y_train):
        lr_model = LogisticRegression()
        lr_model.fit(X_train, y_train)
        return lr_model

    def gbdt_lr_train(self, X_train, y_train):
        self.gbdt_model = self.gbdt_train(X_train, y_train)

        # one_hot
        self.X_train_leafs = self.gbdt_model.apply(X_train)[:, :, 0]
        # print(self.X_train_leafs[0])
        self.gbdt_encoder = OneHotEncoder(categories="auto", sparse=False)
        self.X_transform= self.gbdt_encoder.fit_transform(self.X_train_leafs)
        # print(self.X_transform[0])

        self.lr_model = self.lr_train(self.X_transform, y_train)

    def predict(self, X_test, _test):
        self.X_test_leafs = self.gbdt_model.apply(X_test)[:, :, 0]
        (train_rows, cols) = self.X_train_leafs.shape
        X_trans_all = self.gbdt_encoder.fit_transform(np.concatenate((self.X_train_leafs, self.X_test_leafs), axis=0))

        y_pred = self.lr_model.predict_proba(X_trans_all[train_rows:])[:, 1]
        print(roc_auc_score(y_test, y_pred))

def load_data():
    iris_data = load_iris()
    X = iris_data.data
    y = iris_data.target == 2  # 原结果输出的是 0,1,2 根据是否==2 转化成 0,1
    return train_test_split(X, y, test_size=0.4, random_state=0)

if __name__ == '__main__':
    X_train, X_test, y_train, y_test = load_data()

    gblr = GradientBoostingWithLr()
    gblr.gbdt_lr_train(X_train, y_train)

    gblr.predict(X_test, y_test)