数论——扩展的欧几里德算法 - HDU2669
http://acm.hdu.edu.cn/showproblem.php?pid=2669
#include <iostream>
using namespace std;
int gcd(int a, int b, int &x, int &y) {
) {
x = , y = ;
return a;
}
int q = gcd(b, a%b, y, x);
y -= a / b * x;
return q;
}
int main() {
int a, b;
while (scanf("%d%d", &a, &b) != EOF) {
int x, y;
)
cout << "sorry" << endl;
else {
) {
x += b; y -= a;
}
cout << x << " " << y << endl;
}
}
;
}

这里的x2,y2是递归返回阶段,上一层的y和x,所以代码中的是y-=a/b*x。以21/8为示例,返回阶段递归示意图。

题目要求X必需为非负数,最后这个是很容易忽略掉的,很好看懂,但是写题目的时候没有想到可以这样写。
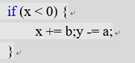

数论——扩展的欧几里德算法 - HDU2669的更多相关文章
- ACM数论之旅4---扩展欧几里德算法(欧几里德(・∀・)?是谁?)
为什么老是碰上 扩展欧几里德算法 ( •̀∀•́ )最讨厌数论了 看来是时候学一学了 度娘百科说: 首先, ax+by = gcd(a, b) 这个公式肯定有解 (( •̀∀•́ )她说根据数论中的相 ...
- (扩展欧几里德算法)zzuoj 10402: C.机器人
10402: C.机器人 Description Dr. Kong 设计的机器人卡尔非常活泼,既能原地蹦,又能跳远.由于受软硬件设计所限,机器人卡尔只能定点跳远.若机器人站在(X,Y)位置,它可以原地 ...
- 欧几里德与扩展欧几里德算法 Extended Euclidean algorithm
欧几里德算法 欧几里德算法又称辗转相除法,用于计算两个整数a,b的最大公约数. 基本算法:设a=qb+r,其中a,b,q,r都是整数,则gcd(a,b)=gcd(b,r),即gcd(a,b)=gcd( ...
- poj2142-The Balance(扩展欧几里德算法)
一,题意: 有两个类型的砝码,质量分别为a,b;现在要求称出质量为d的物品, 要用多少a砝码(x)和多少b砝码(y),使得(x+y)最小.(注意:砝码位置有左右之分). 二,思路: 1,砝码有左右位置 ...
- poj2115-C Looooops(扩展欧几里德算法)
本题和poj1061青蛙问题同属一类,都运用到扩展欧几里德算法,可以参考poj1061,解题思路步骤基本都一样.一,题意: 对于for(i=A ; i!=B ;i+=C)循环语句,问在k位存储系统中循 ...
- poj1061-青蛙的约会(扩展欧几里德算法)
一,题意: 两个青蛙在赤道上跳跃,走环路.起始位置分别为x,y. 每次跳跃距离分别为m,n.赤道长度为L.两青蛙跳跃方向与次数相同的情况下, 问两青蛙是否有方法跳跃到同一点.输出最少跳跃次数.二,思路 ...
- HDU 1576 A/B 扩展欧几里德算法
A/B Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submis ...
- 欧几里德算法及其扩展(推导&&模板)
有关欧几里德算法整理: 1.一些相关概念: <1>.整除性与约数: ①一个整数可以被另外一个整数整除即为d|a(表示d整除a,通俗的说是a可以被d整除),其含义也可以说成,存在某个整数k, ...
- ACM_扩展欧几里德算法
<pre name="code" class="cpp">/* 扩展欧几里德算法 基本算法:对于不完全为 0 的非负整数 a,b,gcd(a,b)表 ...
随机推荐
- SmartGit破解使用的个人方法
转自:https://www.cnblogs.com/nn839155963/p/5912788.html SmartGit是收费的,可以30天的试用期,30天试用期过后,smartgit 需要输入序 ...
- Java学习--jsp内置对象
九个内置对象,其中Out,request,response,session,application常用 get与post区别: request对象: response对象: 请求转发与请求重定向的区别 ...
- div实现水平和垂直都居中的三个超实用的方法
本文仅仅介绍作者认为的三种不错的方式, 方式一:transform: translate(-50%,-50%) 示例代码如下: .div{ position: absolute; top: 50%; ...
- Git简介、安装与配置
老规矩QAQ,先来简单介绍一下Git: Git是一个分布式版本控制系统,可以理解为是一个用于管理代码,控制版本,方便多人合作开发的一款工具. Git:分布式版本控制系统. SVN.CVS:集中式版本控 ...
- eclipse 断点调试快捷键
(1)Ctrl+M --切换窗口的大小(2)Ctrl+Q --跳到最后一次的编辑处(3)F2 --当鼠标放在一个标记处出现Tooltip时候按F2则把鼠标移开时Tooltip还会显示即Show Too ...
- Java基础之基本数据类型的包装类型
Java的基本数据类型的包装数据类型有多种: int Integer,short Short,boolean Boolean,float Float,double Double等等. Java包装类数 ...
- Jsp程序要在Tomcat下运行
首先,回顾下jsp与servlet的区别与联系 JSP经过编译后就成了servlet JSP本质就是Servlet,JVM只能识别java类,不能识别JSP代码,Web容器将JSP代码编译成JVM能够 ...
- Informatica 9.5安装部署
Informatica 结构 1个或多个资源库(Respository) PowerCenter数据整合引擎是基于元数据驱动的,提供了基于数据驱动的元数据知识库(Repository),该元数据知识 ...
- oralce的判断语句
大家对 IF ELSE 语句应该都很熟悉吧,它是用来对过程进行控制的.在 SQL 的世界中 CASE 语句有类似的效果.下面简单的介绍 CASE 语句的用法. CASE 语句的形式 事实上,CASE ...
- 并发编程------->操作系统的发展
手工操作 —— 穿孔卡片 1946年第一台计算机诞生--20世纪50年代中期,计算机工作还在采用手工操作方式.此时还没有操作系统的概念. 程序员将对应于程序和数据的已穿孔的纸带(或卡片)装入输入机,然 ...
