【bzoj2154】Crash的数字表格 莫比乌斯反演

题目描述

今天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时被a和b整除的最小正整数。例如，LCM(6, 8) = 24。回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下：

1  2  3  4  5

2  2  6  4  10

3  6  3  12 15

4  4  12 4  20

看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod 20101009的值。

输入

输入的第一行包含两个正整数，分别表示N和M。

输出

输出一个正整数，表示表格中所有数的和mod 20101009的值。

样例输入

4 5

样例输出

122

---

题解

莫比乌斯反演

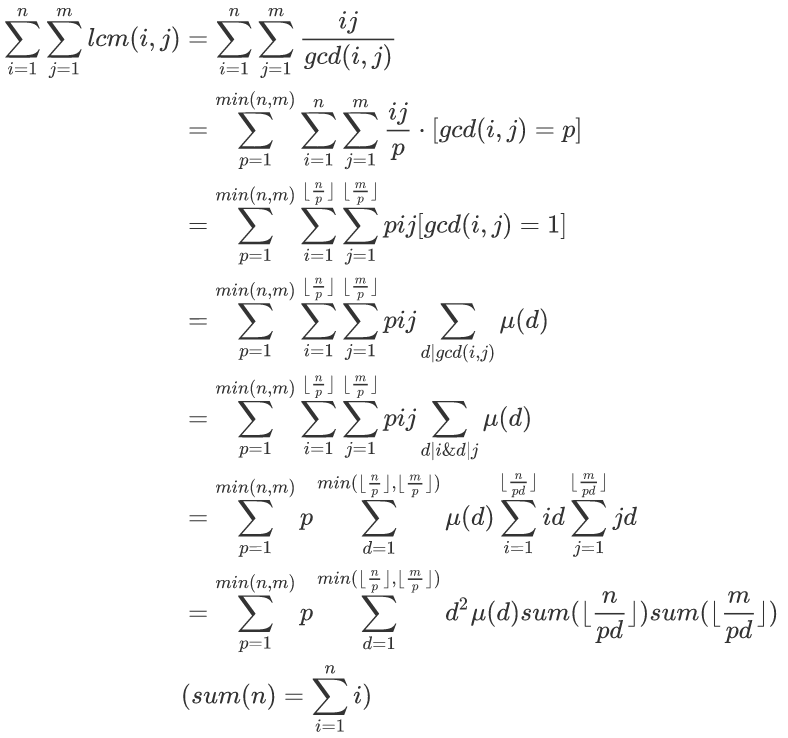
预处理mu和mu(i)*i^2及其前缀和。

然后先分块出n/p和m/p，然后再分块求出后面的一串，这样分块套分块时间复杂度是O(n)的，可以解决这道题。

#include <cstdio>
#include <algorithm>
#define N 10000010
#define mod 20101009
using namespace std;
typedef long long ll;
const int n = 10000000;
int mu[N] , prime[N] , tot;
ll sum[N];
bool np[N];
ll s(int x)
{
	return (ll)x * (x + 1) / 2 % mod;
}
ll query(int a , int b)
{
	int i , last;
	ll ans = 0;
	for(i = 1 ; i <= a && i <= b ; i = last + 1) last = min(a / (a / i) , b / (b / i)) , ans = (ans + (sum[last] - sum[i - 1] + mod) % mod * s(a / i) % mod * s(b / i) % mod) % mod;
	return ans;
}
int main()
{
	int i , j , last , a , b;
	ll ans = 0 , t;
	mu[1] = sum[1] = 1;
	for(i = 2 ; i <= n ; i ++ )
	{
		if(!np[i]) mu[i] = -1 , prime[++tot] = i;
		for(j = 1 ; j <= tot && i * prime[j] <= n ; j ++ )
		{
			np[i * prime[j]] = 1;
			if(i % prime[j] == 0)
			{
				mu[i * prime[j]] = 0;
				break;
			}
			else mu[i * prime[j]] = -mu[i];
		}
		sum[i] = (sum[i - 1] + (ll)mu[i] * i * i + mod) % mod;
	}
	scanf("%d%d" , &a , &b);
	for(i = 1 ; i <= a && i <= b ; i = last + 1) last = min(a / (a / i) , b / (b / i)) , ans = (ans + (s(last) - s(i - 1) + mod) % mod * query(a / i , b / i)) % mod;
	printf("%lld\n" , ans);
	return 0;
}