3D-2D:PnP

PnP(Perspective-n-Point):当知道n个3D空间点及其投影位置时，估计相机位姿。

2D-2D的对极几何方法需要八个或八个以上的点对(以八点法为例),且存在着初始化、纯旋转和尺度的问题。然而,如果两张图像中,其中一张特征点的 3D 位置已知（特征点的 3D 位置可以由三角化,或者由 RGB-D 相机的深度图确定）。那么最少只需三个点对(需要至少一个额外点验证结果)就可以估计相机运动。

因此,在双目或 RGB-D 的视觉里程计中,我们可以直接使用 PnP 估计相机运动。

而在单目视觉里程计中,必须先进行初始化,然后才能使用 PnP。

3D-2D 方法不需要使用对极约束,又可以在很少的匹配点中获得较好的运动估计,是最重要的一种姿态估计方法。

PnP有多种方法求解：直线线性变换（DLT）、P3P还有非线性方法，构建最小二乘问题并迭代求解（Bundle Adjustment）。

直线线性变换（DLT）

空间点P，齐次坐标为$P=\left(X,Y,Z,1\right)^{T}$

在图像$I_1$中，投影到特征点$x_1=\left(u_1,v_1,1\right)^{T}$(归一化平面齐次坐标表示)，并没有用到相机内参K，所以是归一化坐标而不是像素坐标。

定义增广矩阵$\left[R|t\right]$为一个3X4的矩阵，包含旋转与平移信息。

$s\begin{bmatrix} u_1 \\ v_1 \\ 1 \end{bmatrix} = \begin{bmatrix} t_1 & t_2 & t_3 & t_4 \\ t_5 & t_6 & t_7 & t_8 \\ t_9 & t_{10} & t_{11} & t_{12} \end{bmatrix}\begin{bmatrix} X \\ Y \\ Z \\1 \end{bmatrix}$

$su_1 = t_1X + t_2Y + t_3Z + t_4$

$sv_1 = t_5X + t_6Y + t_7Z + t_8$

$s = t_9X + t_{10}Y + t_{11}Z + t_{12}$

把s消去：

$u_1 = \frac{t_1X + t_2Y + t_3Z + t_4}{t_9X + t_{10}Y + t_{11}Z + t_{12}}$,$v_1 = \frac{t_5X + t_6Y + t_7Z + t_8}{t_9X + t_{10}Y + t_{11}Z + t_{12}}$

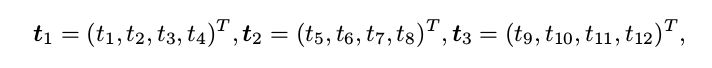
$u_1 =\frac{\textbf{t}_{1}^{T}P}{\textbf{t}_{3}^{T}P}$,$v_1 =\frac{\textbf{t}_{2}^{T}P}{\textbf{t}_{3}^{T}P}$

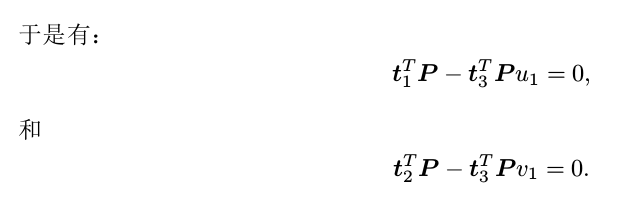
一个特征点提供了两个关于t的约束。

t有１２维，最少需要６对匹配点求$\left[R|t\right]$，为直接线性变换。

可由QR分解完成。

P3P

见书

Bundle Adjustment

除了以上DLT线性方法外，还可以构建非线性最小二乘问题。

线性方法先求相机位姿，再求空间点位置。

非线性优化则把相机位姿和空间点位置都当做优化变量，一起优化。

最小化重投影误差（Reprojection error）

n个三维空间点P及其投影p,位姿为R,t。李代数表示为$\zeta$。

考虑n个三维空间点P及其投影p。

假设某空间点坐标为$P_i = \left[X_i,Y_i,Z_i\right]^{T}$,投影坐标为$u_i=\left[u_i,v_i\right]^{T}$

$exp\left(\zeta^{\wedge}\right)P_i$结果是 4 × 1 的,而它左侧的 K 是 3 × 3 的,所以必须把$exp\left(\zeta^{\wedge}\right)P_i$的前三维取出来,变成三维的非齐次坐标。

将像素坐标（观测到的投影位置）与３D点按照当前估计的位姿进行投影得到的位置相比较得到的误差，即重投影误差。

使用牛顿高斯法需要知道每个误差关于优化变量的导数，也是线性化：

$e\left(x+\Delta\right) \thickapprox e\left(x\right) + J\Delta{x}$,其中e为像素坐标误差。

优化相机位姿$\zeta$

相机坐标系下的空间点坐标$P^{'}$

其中$\delta{\zeta}$是位姿增量相当于牛顿法中的$\Delta{x}$,$e\left(\delta\zeta\oplus\zeta\right)$相于与$f\left(x+\Delta{x}\right)$,f为误差函数，$\oplus$为李代数上的左扰动。

设观测值$\left[u^{'},v^{'}\right]^{T}$。

$e = \left[u^{'}-\left(f_x\frac{X^{'}}{Z^{'}}+c_x\right), v^{'}-\left(f_y\frac{Y^{'}}{Z^{'}}+c_y\right)\right]^{T}$

$P^{'}=\left[X^{'},Y^{'},Z^{'}\right]^{T}$

$\frac{\partial{P}^{'}}{\partial\delta\zeta}=\frac{\partial\left({TP}\right)}{\partial\delta\zeta}$

以下推导过程$p$表示$P$,即空间点。

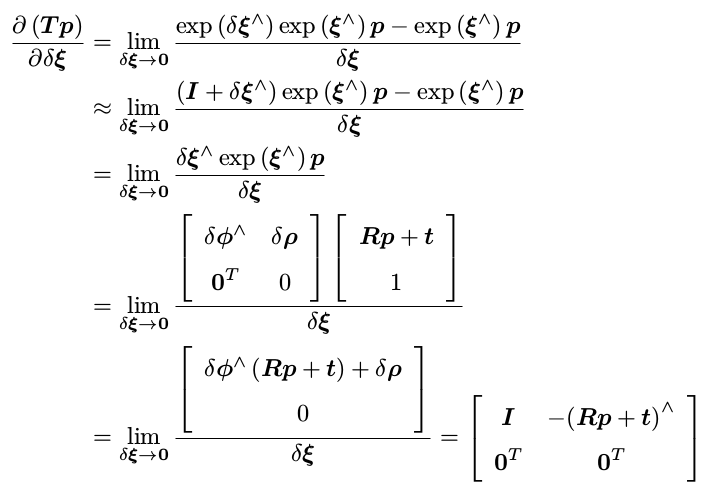
其中$\delta\zeta = \left[\delta\rho,\delta\phi\right]^{T}$,$a^{\wedge}b = -b^{\wedge}a$

优化空间点$P$

其中$\frac{\partial{P{'}}}{\partial{\delta\zeta}}$雅克比的推导方法也可参考：https://blog.csdn.net/zhubaohua_bupt/article/details/74011005

$\delta{\zeta}=\left[\delta\rho,\delta\phi\right]$,$P^{'}=\left[X^{'},Y^{'},Z^{'}\right]$

$\delta{\zeta}=\left[\delta\rho_1,\delta\rho_2,\delta\rho_3,\delta\phi_1,\delta\phi_2,\delta\phi_3\right]$

$\delta{\phi}^{\wedge} = \begin{bmatrix} 0 & -\delta\phi_3 & \delta\phi_2 \\ \delta\phi_3 & 0 & -\delta\phi_1 \\ -\delta\phi_2 & \delta\phi_1 & 0 \end {bmatrix}$

$\delta{\phi}^{\wedge}P^{'}+\delta\rho = \begin{bmatrix} -\delta\phi_3x_2+\delta\phi_2x_3 + \delta\rho_1 \\ \delta\phi_3x_1- \delta\phi_1x_3 + \delta\rho_2 \\ -\delta\phi_2x_1+\delta\phi_1x_2 + \delta\rho_3 \end{bmatrix}$

对$\delta{\zeta}=\left[\delta\rho_1,\delta\rho_2,\delta\rho_3,\delta\phi_1,\delta\phi_2,\delta\phi_3\right]$求导，得$\begin {bmatrix} 1 & 0 & 0 & 0 & -Z^{'} & Y^{'} \\ 0 & 1 & 0 & Z^{'} &  0 & -X^{'} \\ 0 & 0 & 1 & -Y^{'} & X^{'} & 0 \end{bmatrix}$，即$\left[I_{3x3},-P_{3x3}^{'\wedge}\right]$