luogu P1379 八数码难题（A*算法入门详细讲解）

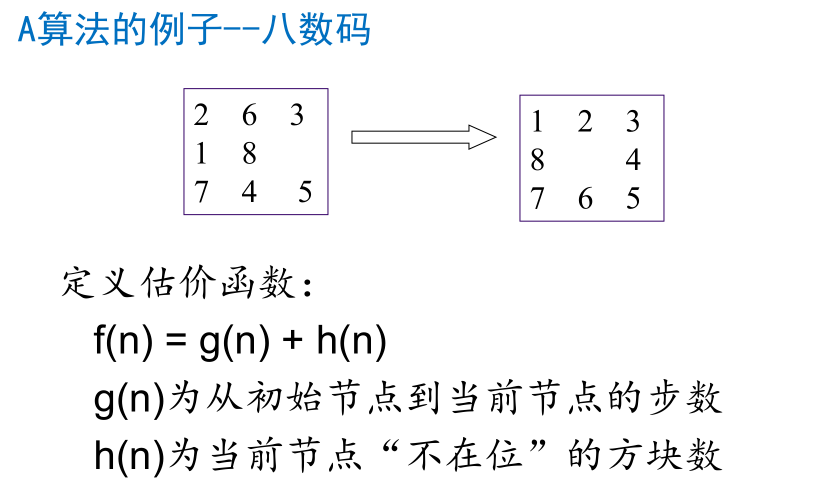
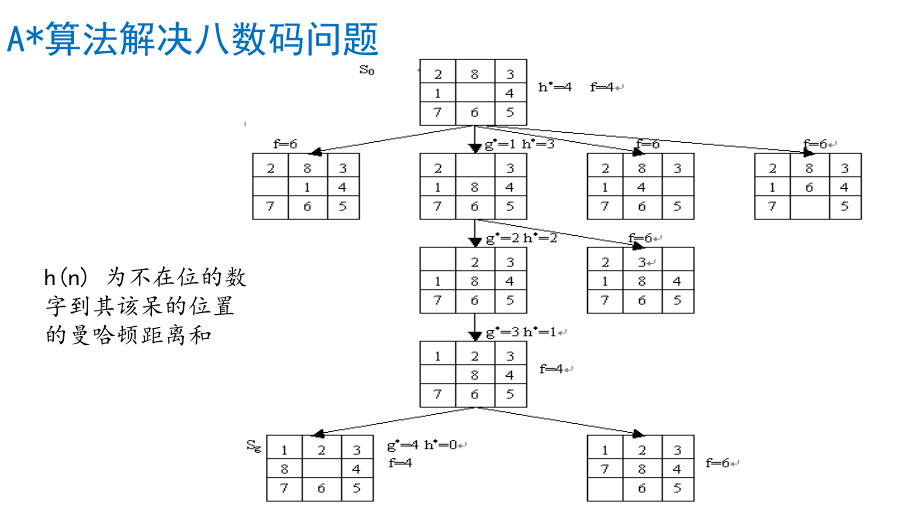
 代码实现细节

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=;
const int dx[]={,,,-};
const int dy[]={,-,,};
int flag,now[N],goal[N];
int dis[N][N],a[N][N],mp[N][N];
inline int calcx(int x){return (x-)/+;}
inline int calcy(int x){return x%?x%:;}
inline int abs(int x){return x>?x:-x;}
inline int h(){int t=;for(int i=;i<=;i++) t+=dis[now[i]][goal[i]];return t;}
inline int check(){for(int i=;i<;i++) if(now[i]!=goal[i]) return ;return ;}
void dfs(int depth,int x,int y,int lim){
    if(depth+h()>lim) return ;
    if(check()){flag=;return ;}
    for(int i=,nx,ny;i<;i++){
        nx=x+dx[i];
        ny=y+dy[i];
        if(flag) return ;
        if(nx>&&nx<=&&ny>&&ny<=){
            swap(a[x][y],a[nx][ny]);swap(now[a[x][y]],now[a[nx][ny]]);
            dfs(depth+,nx,ny,lim);
            swap(a[x][y],a[nx][ny]);swap(now[a[x][y]],now[a[nx][ny]]);
        }
    }
}
void pre(){
    for(int i=;i<=;i++)
        for(int j=i+;j<=;j++)
            dis[i][j]=dis[j][i]=calcx(j)-calcx(i)+abs(calcy(j)-calcy(i));
}
int main(){
    pre();
    goal[]=;goal[]=;goal[]=;goal[]=;goal[]=;goal[]=;goal[]=;goal[]=;goal[]=;
    int sx,sy;
    for(int i=,x,y,z;i<=;i++){
        scanf("%1d",&z);
        x=calcx(i);y=calcy(i);
        mp[x][y]=z;now[z]=i;
        if(!z) sx=x,sy=y;
    }
    for(int i=;;i++){
        memcpy(a,mp,sizeof mp);
        dfs(,sx,sy,i);
        if(flag){printf("%d\n",i);break;}
    }
    return ;
}