如何通俗理解贝叶斯推断与beta分布？

有一枚硬币（不知道它是否公平），假如抛了三次，三次都是“花”：

能够说明它两面都是“花”吗？

1 贝叶斯推断

按照传统的算法，抛了三次得到三次“花”，那么“花”的概率应该是：

但是抛三次实在太少了，完全有可能是运气问题。我们应该怎么办？

托马斯·贝叶斯（1702－1761），18世纪英国数学家，1742年成为英国皇家学会会员。

贝叶斯认为在实验之前，应根据不同的情况对硬币有所假设。不同的假设会得到不同的推断。

比如和滑不溜手的韦小宝玩。韦小宝可能拿出各种做过手脚的硬币，让我们猜不透，只能假设对硬币一无所知。这种假设之下，我们就只能根据实验结果来猜测。

因此，实验结果是“扔三次，三次花”，倾向于认为韦小宝有可能作弊：

大侠陈近南用的可能是公平硬币：

而憨坏的多隆，真的有可能用两面“花”来和你玩：

各种假设称为先验分布，结合刚才“扔三次，三次花”的实验数据，推断出硬币的后验分布，这就是贝叶斯推断：

这里补充一下，可能大家觉得再多抛几次硬币就可以了，何必弄什么贝叶斯推断。不过现实生活中有一些事件不是能够多“抛”几次的，比如地震、彗星撞击地球等等。这里只是借着硬币来讨论问题。

2  分布

那么问题来了，“先验分布”，“后验分布”用数学怎么表示：

对于扔硬币， 分布非常适合用来完成这个任务。

2.1 先验分布

 分布简记为（这一节里面的所有细节会在后面给出）：

根据 参数的不同，形态各异：

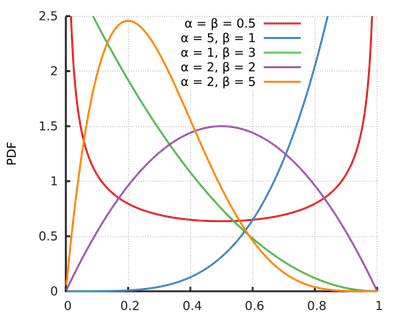
这个特性非常适合用来做先验分布。比如，在韦小宝面前，我们对硬币一无所知。

贝叶斯说一无所知也就是意味着任何概率都是一样的，都是有可能的，所以选用均匀分布（所谓的无信息先验，可以参看这篇文章）：

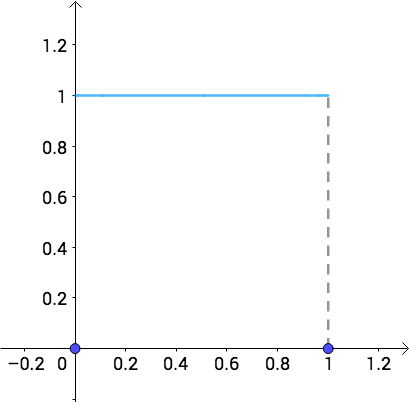
 正好就是均匀分布：

正直的陈近南，可能用的是公平硬币，也就是说概率在0、1之间（0表示“字”，1表示“花”）， 可以表示这样的分布：

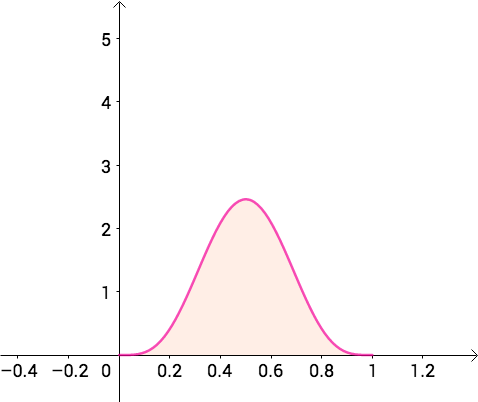
而憨坏的多隆，可能用了两面花，也就是说概率可能集中到1附近， 可以表示这样的分布：

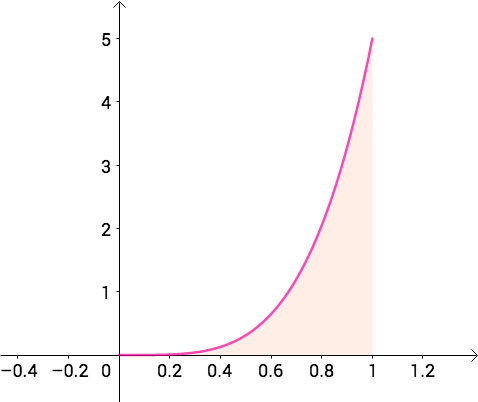
也就是说可以用 分布来模拟各种先验分布：

• 一无所知：
• 公平硬币：
• 两面花：

2.2 后验分布

用 分布来模拟扔硬币的先验分布之后，通过贝叶斯推断，得到的后验分布依然是 分布：

具体到这里：

再具体到韦小宝的情况就是：

其中，用 来表示实验数据，意思是3次花，0次字（ 就是2次花，1次字）。

图像上的变化就是：

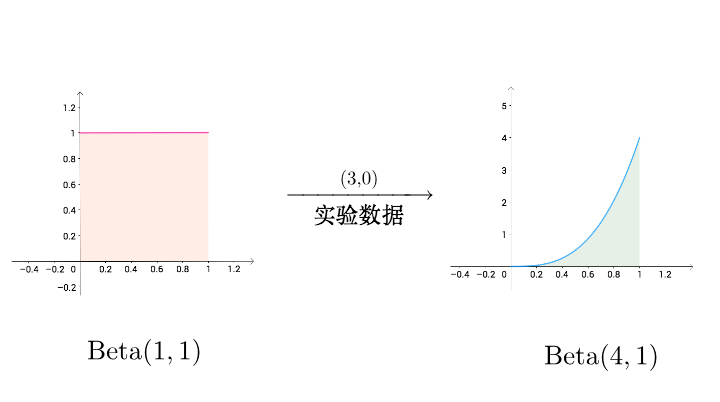
可以看到，作弊的可能性还是比较大的。

陈近南的情况：

结合实验数据之后，图像的中心从0.5往0.6方向移动了，作弊可能性有所增加，不过总体来看应该还是公平硬币的可能性大。

多隆的情况：

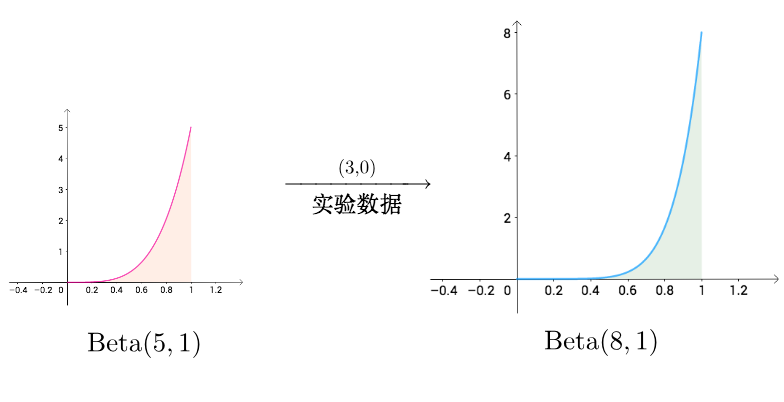
更向1集中，作弊的可能性非常高。

3 代数细节

3.1 贝叶斯推断

贝叶斯推断：

的应用到二项式分布的数学细节如下。假设实验数据 服从二项分布：

上面的式子根据贝叶斯定理（离散贝叶斯可以参看怎样用非数学语言讲解贝叶斯定理（Bayes theorem）？，连续贝叶斯可以参看这里）可以表示为：

其中 为“花”的次数。分母与实验数据无关，可以视作常数：

因此，写成下面这样更容易看清楚重点（其中 表示两者之间成比例）：

3.2  分布

 长成这个样子：

其中， 为 函数。

随着 的变换， 分布形态各异：

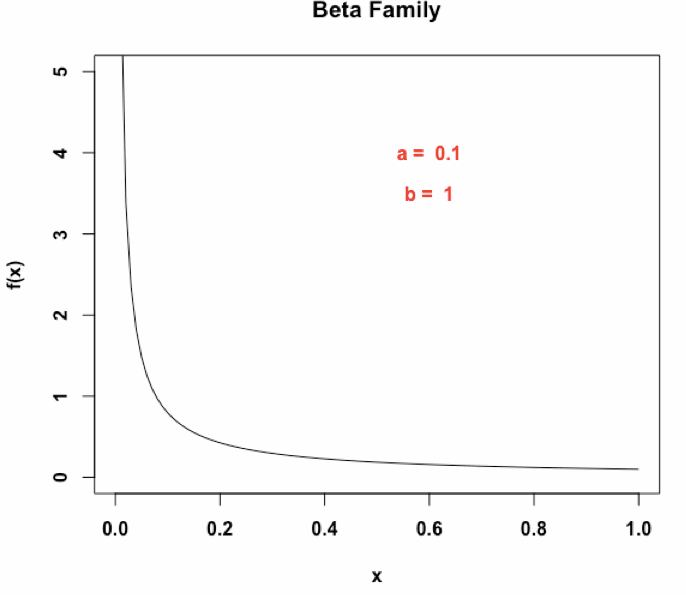
3.3 共轭先验

对于二项式分布，用 分布作为先验分布，通过贝叶斯推断之后，后验分布依然是 分布：

这种特性称为共轭先验。

并且：

关于这点的证明请参看这里，需要***。

文章最新版本在（有可能会有后续更新）：如何理解贝叶斯推断，beta分布？