【RL系列】从蒙特卡罗方法步入真正的强化学习

蒙特卡罗方法给我的感觉是和Reinforcement Learning: An Introduction的第二章中Bandit问题的解法比较相似，两者皆是通过大量的实验然后估计每个状态动作的平均收益。不过两者的区别也是显而易见，Bandit问题比较简单，状态1->动作1->状态1，这个状态转移过程始终是自我更新的过程，而且是一一对应的关系。蒙特卡罗方法所解决的问题就要复杂一些，通常来说，其状态转移过程可能为，状态1->动作1->状态2->动作1->状态3。Sutten书中是这样描述两者的区别：

The main difference is that now there are multiple states, each acting like a different bandit problem (like an associative-search or contextual bandit) and that the different bandit problems are interrelated.

这里说的很好，应用蒙特卡罗方法的问题中的每一个状态下的其中一个动作之后的状态转移过程都像是许多个不同的Bandit问题。还有一个很明显的区别是，蒙特卡罗问题大都有一个或几个明确的目标状态，达到目标状态后，才能计算当前收益，中间过程通常来说并没有自己的状态或动作收益，但对于Bandit问题来说是没有这个中间过程的。

什么是中间过程？简单来说就是从起始状态到达目标状态中间所经历的状态动作集合。在蒙特卡罗方法中，中间过程不获得任何奖励，但是中间过程的状态动作价值可以由目标状态奖励进行估计。这个估计的原则也很简单，可以描述为：某状态动作价值可以估计为经过该状态到达目标所获得的奖励之和除以经过该状态的次数。对于某个中间过程的状态动作价值估计实际上就是许多个不同的Bandit问题中的一个。在上一篇文章中提到了在解决Soap Bubble问题中，蒙特卡罗方法的优势，即可以快速收敛某一个状态或某几个状态的价值估计。上一篇文章中的算法只关注起始状态的价值收敛而完全忽略中间过程，但当使用蒙特卡罗方法估计所有状态价值时，对中间过程不进行任何处理的方法就太低效了。所以下面我们尝试将中间状态价值估计应用到之前的算法中，看一看完整的蒙特卡罗方法进行价值估计的算法流程，还是以Soap Bubble为例（什么是Soap Bubble问题，可以参考上一篇博文【RL系列】蒙特卡罗方法——Soap Bubble）：

1. 投影闭合曲线到x-y平面
2. 开始迭代，随机选择起始点(x, y)
3. 随机选择动作开始游走
4. 判断是否碰到边界，如碰到边界，记录边界高度值$ H_b $，并记录中间经过的每一个状态，写成状态集合$S$。未碰到则继续游走。
5. 设状态state属于状态集合$ S $，用公式更新状态state的价值总和$ V(\mathrm{state}) $与经过状态state的次数$ C(\mathrm{state}) $：$$ V(\mathrm{state}) =  V(\mathrm{state}) + H_b \\ C(\mathrm{state}) =  C(\mathrm{state}) + 1$$
6. 回到第三步重新开始迭代。经过大量次数的实验后，停止循环过程。
7. 任何一点（任何一个状态）的高度值的估计可以计算估计为((x, y) = state)：$$ H(state) = \frac{V(state)}{C(state)} $$

这个加入中间过程估计的逻辑还是很简单的，因为蒙特卡罗方法有一条非常重要的性质，“每一个状态的估计都是独立的，不依赖于其它状态的! ”，所以你可以把中间过程某个状态的估计看成是该状态作为起始状态的估计。迭代开始之初对起始状态的随机选择也十分重要，随机选择是为了保证每个装填都有作为起始状态的机会，也是为了增加每一个状态被访问的机会，这种策略叫做Exploring Starts，当其同时运用到动作选择时，才是完整的Monte Carlo ES算法（这个算法也是Monte Carlo经典问题BlackJack的求解基础！）。

直接给出该算法的计算结果：

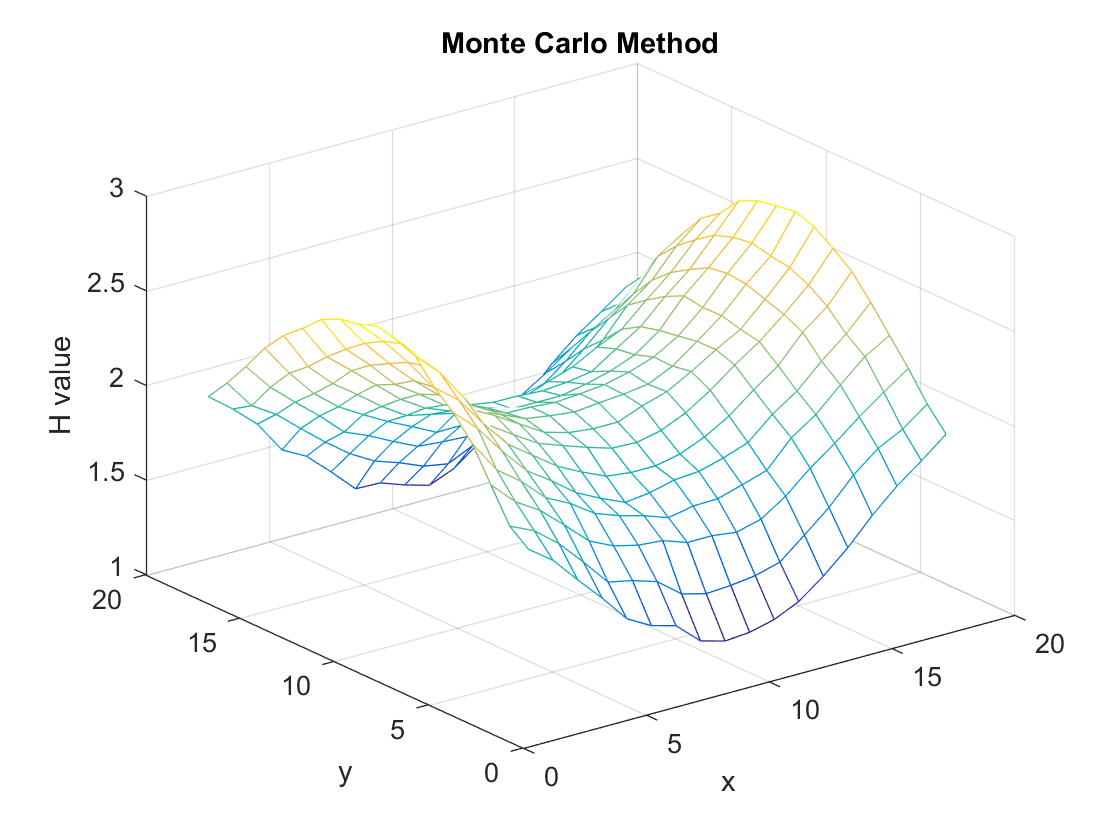
经过10000次迭代，效果还是不错的，但相比于大约250次迭代就可以计算出更加精确值的Iteration Method来说还是效率较低的。Iteration Method的本质就是Dynamic Programming，在强化学习中相对应就是马尔可夫决策——一种建立在模型，状态与状态之间关系的算法。Monte Carlo最大的优势在于，不需要模型，只靠探索+总结就可以寻找到最优策略，这比马尔可夫决策更加的趋近于人类的决策行为，真正的人工智能之强化学习是从这里开始的。