[BUUCTF]REVERSE——[GUET-CTF2019]re

[GUET-CTF2019]re

附件

步骤：

1. 查壳儿，upx壳，64位程序
   

2. upx脱壳儿，然后扔进64位ida,通过检索字符串，找到有关flag的信息定位到关键函数
   
   让我们输入flag，然后满足sub_4009AE函数提示correct！

3. 看一下sub_4009AE函数
   
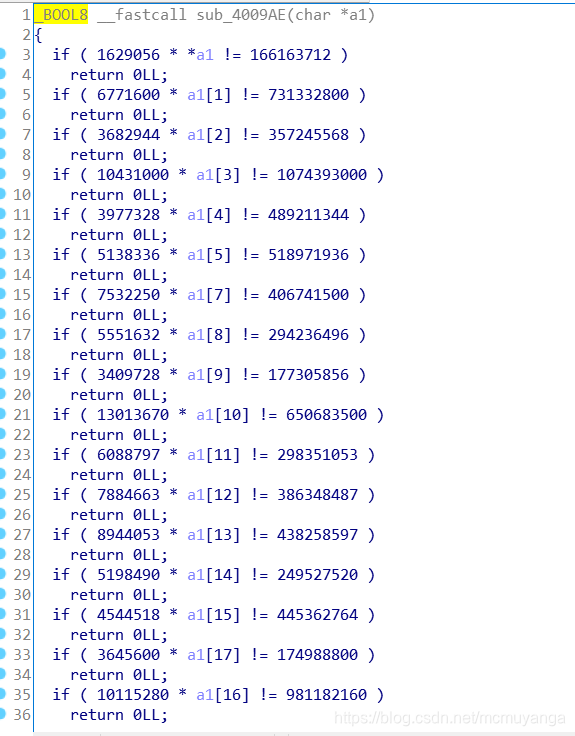
   对我门输入的flag字符串每一位*一个数据，然后进行了判断，除一下就可以算出flag的每一位

exp：

a1 = chr(166163712 // 1629056)
a2 = chr(731332800 // 6771600)
a3 = chr(357245568 // 3682944)
a4 = chr(1074393000 // 10431000)
a5 = chr(489211344 // 3977328)
a6 = chr(518971936 // 5138336)
a8 = chr(406741500 // 7532250)
a9 = chr(294236496 // 5551632)
a10 = chr(177305856 // 3409728)
a11 = chr(650683500 // 13013670)
a12 = chr(298351053 // 6088797)
a13 = chr(386348487 // 7884663)
a14 = chr(438258597 // 8944053)
a15 = chr(249527520 // 5198490)
a16 = chr(445362764 // 4544518)
a17 = chr(981182160 // 10115280)
a18 = chr(174988800 // 3645600)
a19 = chr(493042704 // 9667504)
a20 = chr(257493600 // 5364450)
a21 = chr(767478780 // 13464540)
a22 = chr(312840624 // 5488432)
a23 = chr(1404511500 // 14479500)
a24 = chr(316139670 // 6451830)
a25 = chr(619005024 // 6252576)
a26 = chr(372641472 // 7763364)
a27 = chr(373693320 // 7327320)
a28 = chr(498266640 // 8741520)
a29 = chr(452465676 // 8871876)
a30 = chr(208422720 // 4086720)
a31 = chr(515592000 // 9374400)
a32 = chr(719890500 // 5759124)

print (a1,a2,a3,a4,a5,a6,a8,a9,a10,a11,a12,a13,a14,a15,a16,a17,a18,a19,a20,a21,a22,a23,a24,a25,a26,a27,a28,a29,a30,a31,a32)

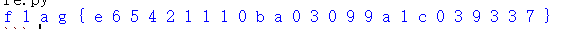
这里少了一位a7，爆破一下，得出a7=1
flag{e165421110ba03099a1c039337}