Something about 树链剖分

声明：部分思路与图片源于OI Wiki

关于树链剖分

树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。

树链剖分有多种形式，如 重链剖分，长链剖分 和用于 $LCT$ 的剖分，大多数情况下，“树链剖分”都指“重链剖分”。

重链剖分可以将树上的任意一条路径划分成不超过$O(\log n)$条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的$LCA$为链的一个端点）。

重链剖分还能保证划分出的每条链上的节点$DFS$序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。

如：

1.修改 树上两点之间的路径上 所有点的值。

2.查询 树上两点之间的路径上 节点权值的 和/极值/其它（在序列上可以用数据结构维护，便于合并的信息）

除了配合数据结构来维护树上路径信息，树剖还可以用来$O(\log n)$（且常数较小）地求$LCA$。在某些题目中，还可以利用其性质来灵活地运用树剖。

重链剖分

给出以下定义：

定义 重子节点 表示其子节点中子树最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子节点，就无重子节点。

定义 轻子节点 表示剩余的所有子结点。

从这个结点到重子节点的边为重边。

到其他轻子节点的边为轻边。

若干条首尾衔接的重边构成重链。

把落单的结点也当作重链，那么整棵树就被剖分成若干条重链。

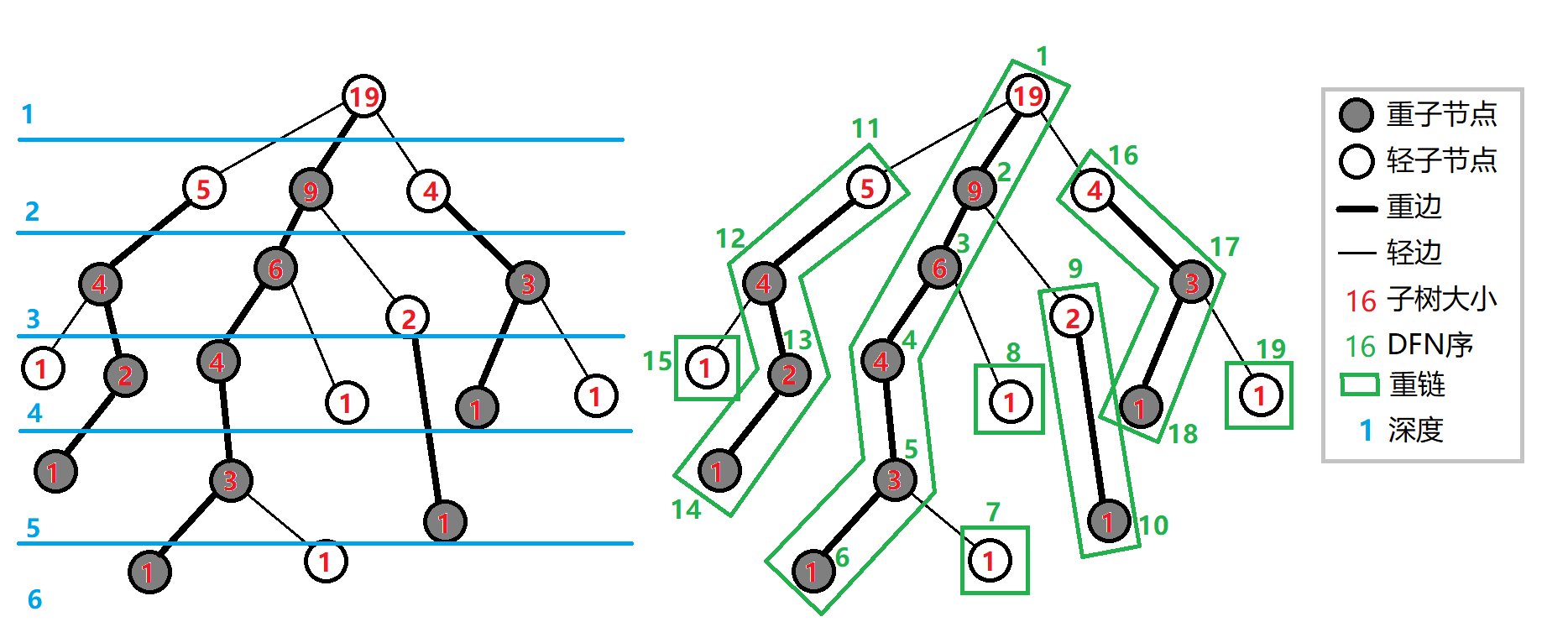
实现

做出以下说明：

$Ftr_x$表示节点$x$在树上的父亲。

$Dep_x$表示节点$x$在树上的深度。

$Size_x$表示节点$x$的子树的节点个数。

$Son_x$表示节点$x$的重儿子。

$Top_x$表示节点$x$所在重链的顶部节点（深度最小）。

$Dfn_x$表示节点$x$的 $DFS$ 序，也是其在线段树中的编号。

$Rank_x$表示 $DFS$ 序所对应的节点编号，有$Rank_{Dfn_x}=x$ 。

我们进行两遍 DFS 预处理出这些值，其中第一次$DFS$求出 $Ftr_x$，$Dep_x$，$Size_x$，$Son_x$，第二次 DFS 求出 $Top_x$，$Dfn_x$，$Rank_x$。

inline void DFS1(int o)

{

    Son[o] = -1;

    Size[o] = 1;

    for (register int j = h[o]; j; j = nxt[j])

        if (!Dep[p[j]])

        {

            Dep[p[j]] = Dep[o] + 1;

            Ftr[p[j]] = o;

            DFS1(p[j]);

            Size[o] += Size[p[j]];

            if (Son[o] == -1 or Size[p[j]] > Size[Son[o]])

                Son[o] = p[j];

        }

}

inline void DFS2(int o , int t)

{

    Top[o] = t;

    Dfn[o] = ++Cnt;

    Rank[Cnt] = o;

    if (Son[o] == -1)

        return;

    DFS2(Son[o] , t);

    for (register int j = h[o]; j; j = nxt[j])

        if (p[j] != Son[o] and p[j] != Ftr[o])

            DFS2(p[j] , p[j]);

}

重链剖分性质

树上每个节点都属于且仅属于一条重链。

重链开头的结点不一定是重子节点（因为重边是对于每一个结点都有定义的）。

所有的重链将整棵树 完全剖分。

在剖分时重边优先遍历，最后树的$DFN$序上，重链内的$DFN$序是连续的。按$DFN$排序后的序列即为剖分后的链。

一颗子树内的$DFN$序是连续的。

可以发现，当我们向下经过一条轻边时，所在子树的大小至少会除以二。

因此，对于树上的任意一条路径，把它拆分成从$LCA$分别向两边往下走，分别最多走$O(\log n)$次，因此，树上的每条路径都可以被拆分成不超过$O(\log n)$条重链。

(待更新)