串的模式匹配 BF算法和KMP算法

设有主串s和子串t，子串t的定位就是要在主串中找到一个与子串t相等的子串。通常把主串s称为目标串，把子串t称为模式串，因此定位也称为模式匹配。

模式匹配成功是指在目标串s中找到一个模式串t；
不成功则指目标串s中不存在模式串t

Brute-Force算法

采用穷举的思路，从目标串s的第一个字符开始和模式串t的第一个字符开始比较

若相等，则继续逐个比较后续字符
不相等则从目标串s的第二个字符开始重新与模式串t的第一个字符进行比较

若匹配成功则返回主串中第一次出现模式串的位置，匹配失败返回-1

以目标串"abcdefgab"，模式串"abcdex"为例

匹配次数	位置	结果
第1.1次匹配	i = 0，j = 0	a = a
1.2	i = 1，j = 1	b = b
1.3	i = 2，j = 2	c = c
1.4	i = 3，j = 3	d = d
1.5	i = 4，j = 4	e = e
1.6	i = 5，j = 5	f ≠ x
第2次匹配	i = 1，j = 0	b ≠ a
第3次匹配	i = 2，j = 0	c ≠ a
第4次匹配	i = 3，j = 0	d ≠ a
第5次匹配	i = 4，j = 0	e ≠ a
第6次匹配	i = 5，j = 0	f ≠ a
第7次匹配	i = 6，j = 0	g ≠ a
第8.1次匹配	i = 7，j = 0	a = a
8.2	i = 8，j = 1	b = b

当i = 9时，目标串下标越界，匹配结束。
结束时j没有指向模式串尾，说明没有匹配成功。返回-1

BF算法的实现

int
BF_index( char *s1, char *s2 )
{
	int i = 0, j = 0;
	int s1_len = strlen(s1);
	int s2_len = strlen(s2);
	while( i < s1_len  && j < s2_len ){
		if( s1[i] == s2[j] ){
			i++;
			j++;
		}else{
			i = i - j + 1;
			j = 0;
		}
	}
	if( j >= s2_len ){
		return ( i - s1_len );
	}else{
		return -1;
	}
}

最好时间复杂度为O( s2_len )
最坏时间复杂度为O( s1_len × s2_len )
平均时间复杂度为O( s1_len × s2_len )

这个算法简单易于理解，但效率不高，主要原因是：主串指针i在若干个字符序列比较相等后，若有一个字符比较不相等仍需回溯，重复做前面的事情。

KMP算法

引用了《大话数据结构》第5章KMP算法的内容

KMP算法专门针对BF算法中主串指针的回溯的问题进行优化，极大的提高了模式匹配算法的效率

例一

以目标串S"abcdefgab"，模式串T"abcdex"为例

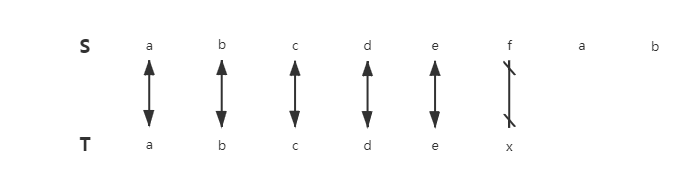
首先，模式串T有一个特点：首字符a仅在T[0]出现，后面的字符和T[0]均不相等。

第一次匹配的结果显示

[

]

[

]

(

)

S[i] = T[i]( i = 0,1, 2, 3, 4 )

S[i]=T[i](i=0,1,2,3,4)
由这个结果得出，在S串中的a也只在S[0]出现，这意味着S[1]、S[2]、S[3]、S[4]都不是a，这是可以直接得出的结论，所以在BF算法中的第2, 3, 4, 5次匹配都是多余的。

这里是KMP算法的关键。我们知道T串中首字符a与它后面的字符均不相等，然后通过判断得出T[1] = S[1]，则可以省略BF算法的第2次匹配。同理，T[2]、T[3]、T[4]与S对应位置的字符判断相等后，也可以省略掉对应的匹配操作。

第6次匹配不能省略，因为在第1.6次匹配时只得出了S[5]≠T[5]，没有得出S[5] ≠ T[0]，所以这一步判断S[5]和T[0]需要保留，j变为0。

首字符仅在T[0]出现的情况比较特殊，下面讨论较一般的情况，即除了串首之外，首字符还分布在模式串不同的位置。

例二

以目标串abcababca，模式串abcabx为例

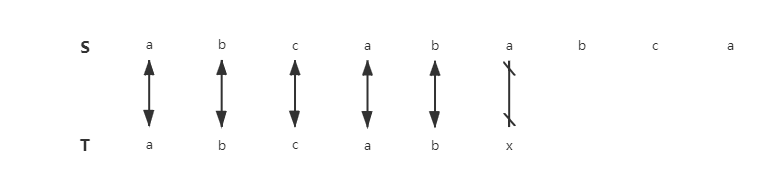
和例一相似，模式串T的特征是：首字符a出现的位置不唯一，分别是T[0]和T[3]

第一次匹配结果

[

]

[

]

(

)

S[i] = T[i]( i = 0,1, 2, 3, 4 )

S[i]=T[i](i=0,1,2,3,4)

T[0] ≠ T[1]，省略BF算法的第2次匹配
T[0] ≠ T[2]，省略BF算法的第3次匹配

T[0] = T[3]，T[1] = T[4]，而在第一次匹配我们已经知道T[3] = S[3]，T[4] = S[4]，即S[3] = T[0]，S[4] = T[1]。而BF算法做多了两次匹配才得出相等的结论，显然第4次、第5次匹配是多余的。

在BF算法中，目标串指针i是不断地往回走的，在KMP算法中i不往后走，而是让模式串T的指针j变化。

j值的变化取决于T串中是否有重复的部分

把T串各个位置j值的变化定义为一个数组next，那么next的长度就是T串的长度。

模式串T中存在某个k( 0 < k < j )，使得以下等式成立

“

−

”

“

−

”

“T_0T_1...T_{k-1}”=“T_{j-k}T_{j-k+1}...T_{j-1}”

“T0T1...Tk−1”=“Tj−kTj−k+1...Tj−1”
例如，T=ababc，当j=4时，T[ j ] = c，有T[0]T[2-1] = T[4-2]T[4-2+1]，k = 2，所以next[4] = k
= 2

归纳起来就是

[

]

{

−

当

时

max

⁡

{

∣

且

“

−

”

“

−

”

}

当

此

集

合

不

为

空

时

其

他

情

况

next[j] =x = \begin{cases} -1, 当j=0时\\ \max\{k | 0<k<j, 且“T_0T_1...T_{k-1}”=“T_{j-k}T_{j-k+1}...T_{j-1}”\}当此集合不为空时\\ 0其他情况 \end{cases}

next[j]=x=⎩⎪⎨⎪⎧−1,当j=0时max{k∣0<k<j,且“T0T1...Tk−1”=“Tj−kTj−k+1...Tj−1”}当此集合不为空时0其他情况

推导next数组

T = `abcdex`

j	0	1	2	3	4	5
T[ j ]	a	b	c	d	e	x
next[ j ]	-1	0	0	0	0	0

j = 0，next[0] = -1
j = 1，0 < k < 1，下标不能是小数，属于其他情况，next[1] = 0
j = 2，k = 1，此时从0到k-1只有T[0]，T[0] ≠ T[1]，属于其他情况，next[2] = 0
j = 3，k = 1或2，当k = 2时，T[0]T[1] ≠ T[1]T[2]，属于其他情况，next[3] = 0

同理，最终得到T的next数组为-1，0，0，0，0，0

T = `abcabx`

j	0	1	2	3	4	5
T[ j ]	a	b	c	a	b	x
next[ j ]	-1	0	0	0	1	2

j = 0，next[0] = -1
j = 1，同上说明，next[1] = 0
j = 2，k = 1，同上，next[2] = 0
j = 3，k = 1或2，同上，next[3] = 0
j = 4，k = 1或2或3，当k = 1时，T[0] = T[3]，next[4] = 1
在后续的计算可以不用按照定义求解，从j-1出发，看能有多少个字符和T串开头匹配即可
j = 5，有T[0]T[1] = T[3]T[4]，得到 k = 2，next[j] = 2

最终next数组为-1，0，0，0，1，2

T = `ababaaaba`

j = 0，next[0] = -1
j = 1，同上，next[1] = 0
j = 2，同上，next[2] = 0
j = 3，有T[0] = T[2]，next[3] = 1
j = 4，有T[0]T[1] = T[2]T[3]，next[4] = 2
j = 5，有T[0]T[1]T[2] = T[2]T[3]T[4]，next[5] = 3
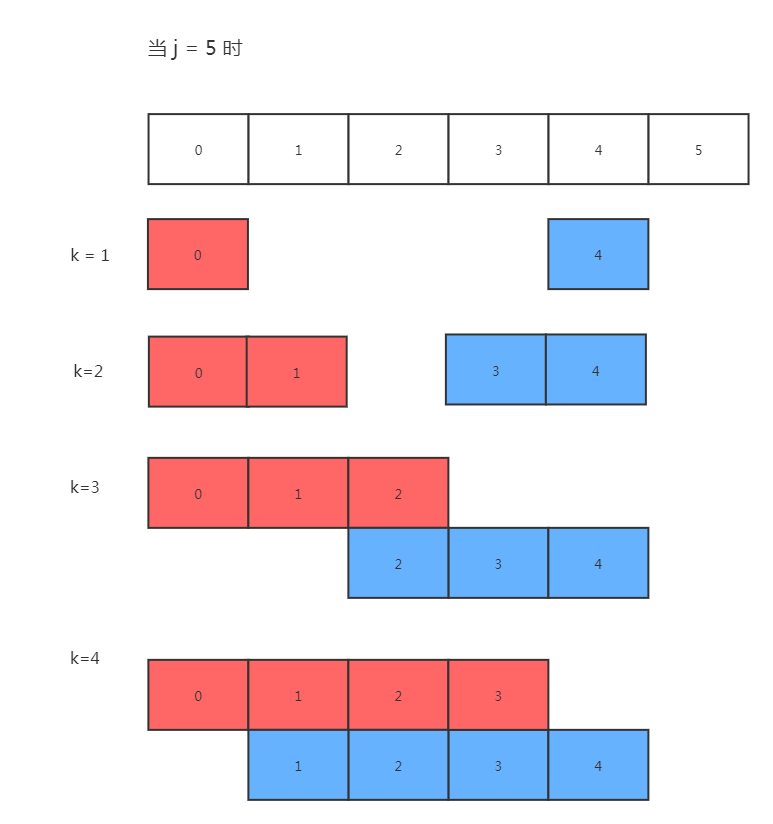
j = 6，有T[0] = T[5]，next[6] = 1
j = 7，有T[0] = T[6]，next[7] = 1
j = 8，有T[0]T[1] = T[6]T[7]，next[8] = 2

next数组为-1，0，0，1，2，3，1，1，2

T = `aaaaaaaab`

j = 0，next[0] = -1
j = 1，next[1] = 0
j = 2，T[0] = T[1]，next[2] = 1
j = 3，取k最大的情况即T[0]T[1] = T[1]T[2]，next[3] = 2
…
j = 8，next[8] = 7

next数组为-1，0，1，2，3，4，5，6，7

到这里就可以解释next[j] = k的含义了，这个等式表示模式串T[j]之前已经有k个字符成功匹配，下一次应该从T[k]开始匹配，而next[j] = -1表示T串当前没有加速匹配的信息，加1，下一次从0开始判断。

KMP算法的实现

void
KMP_getNext( char *s1, int *next )
{
	int j = 0, k = -1;
	next[0] = -1;
	while( j < strlen(s1) - 1 ){
		if( k == -1 || s1[j] == s1[k] ){
			j++;
			k++;
			next[j] = k;
		}else{
			k = next[k];
		}
	}
}
int
KMP_index( char *s1, char *s2 )
{
	int i = 0, j = 0;
	int next[MAXSIZE];
	int s1_len = strlen(s1);
	int s2_len = strlen(s2);
	KMP_getNext( s1, next );
	while( i < s1_len && j < s2_len ){
		if( j == -1 || s1[i] == s2[j] ){
			i++;
			j++;
		}else{
			j = next[j];
		}
	}
	if( j >= s2_len ){
		return ( i - s2_len );
	}else{
		return -1;
	}
}

求next数组的时间复杂度为O(s2_len)，KMP算法匹配时不回溯，则整体算法时间复杂度为O( s2_len + s1_len )

需要强调的是，KMP算法仅当T串和S串之间有许多部分匹配的情况下才体现出它的优势。

例题

已知字符串S为"abaabaabacacaabaabcc"，模式串T为"abaabc"，采用KMP算法进行匹配，第一次出现“失配”（s[i] != t[j]）时，i = j = 5，则下次开始匹配时，i和j的值分别是

题目要求采用KMP算法，主串指针不回溯，i = 5，通过推导next数组找到next[j]

j	0	1	2	3	4	5
T[ j ]	a	b	a	a	b	c
next[ j ]	-1	0	0	1	1	2

得到next[5] = 2
综上，i = 5, j = 2

改进的KMP算法

以S="aaaabcde"，T="aaaaax"为例

求出next数组为-1、0、1、2、3、4。

当 i = 4，j = 4时，S[4] ≠ T[4]，于是j = next[j]，得到 j = 3。S[4] ≠ T[3]，j = next[j]，得到 j = 2…一直回退到 j = 0，才能i++，j++，得到 i = 5，j = 0

用首位next[0]的值去代替与它相同的字符后续的next[j]的值可以省去上面回退的过程。

推导nextval数组

T = `"ababaaaba"`

先推导出next数组：-1，0，0，1，2，3，1，1，2

j = 0，nextval[0] = -1
j = 1，next[1] = 0，T[1] ≠ T[0]，nextval[1] = next[1] = 0，保持不动
j = 2，next[2] = 0，T[2] = T[0]，所以nextval[2] = nextval[0] = -1
j = 3，next[3] = 1，T[3] = T[1]，所以nextval[3] = nextval[1] = 0
j = 4，next[4] = 2，T[4] = T[2]，所以nextval[4] = nextval[2] = -1
j = 5，next[5] = 3，T[5] ≠ T[3]，所以nextval[5] = next[5] = 3
j = 6，next[6] = 1，T[6] ≠ T[1]，所以nextval[5] = next[5] = 1
j = 7，next[7] = 1，T[7] = T[1]，所以nextval[7] = nextval[1] = 0
j = 8，next[8] = 2，T[8] = T[2]，所以nextval[8] = nextval[2] = -1

最终得到nextval数组为 -1， 0， -1， 0， -1， 3， 1， 0， -1

T = `"aaaaax"`

求出next数组为-1、0、1、2、3、4。

j = 0，nextval[0] = -1
j = 1，next[1] = 0，T[1] = T[0]，nextval[1] = nextval[0] = -1
j = 2，next[2] = 1，T[2] = T[1]，nextval[2] = nextval[1] = -1
…
j = 5，next[5] = 4，T[5] ≠ T[4]，nextval[5] = next[5] = 4，保持不动

最终求出nextval数组为 -1，-1，-1，-1，-1，4