定义

  • 递归是一种解决问题的方法，它把一个问题分解为越来越小的子问题，直到问题的规模小到可以被很简单直接解决。
  • 通常为了达到分解问题的效果，递归过程中要引入一个调用自身的函数。

举例

  • 数列求和
  1. def listsum(numlist):
  2.     if len(numlist) == 1:
  3.         return numlist[0]
  4.     else:
  5.         return numlist[0]+listsum(numlist[1:])
  7. if __name__ == "__main__":
  8.     print(listsum([1, 3, 5, 7, 9]))

递归三大定律

就像阿西莫夫（l.Asimov） 的“机器人三定律”一样，递归算法也要遵循三条重要的定律：

  • 递归算法必须有个基本结束条件
  • 递归算法必须改变自己的状态并向基本结束条件演进
  • 递归算法必须递归地调用自身

应用

整数转换为任意进制

  1. def toStr(n, base):
  2.     convertString = "0123456789ABCDEF"
  3.     if n < base:
  4.         return convertString[n] # 最小规模
  5.     else:
  6.         return toStr(n//base,base)+convertString[n % base] # 减小规模，调用自身
  8. if __name__ == "__main__":
  9.     print(toStr(10,2))
  10.     print(toStr(255,16))

递归调用的实现

  • 当一个函数被调用的时候，系统会把调用时的现场数据压入到系统调用栈

    • 每次调用，压入栈的现场数据成为栈帧
    • 当函数返回时，要从调用栈的栈顶取得返回地址，恢复现场，弹出栈帧，按地址返回

  • 易碰到错误：RecursionError

    • 递归的层数太多，系统调用栈容量有限
    • 递归深度限制
      • 检查程序中是否忘记设置基本结束条件，导致无限递归
      • 或者向基本结束条件演进太慢，导致递归层数太多，调用栈溢出
    • 在python内置的sys模块可以获取和调整最大递归深度
    1. import sys
    2. sys.getrecursionlimit()#默认1000
    3. sys.setrecursionlimit(3000)#自定义设置
    4. sys.getrecursionlimit()

递归可视化

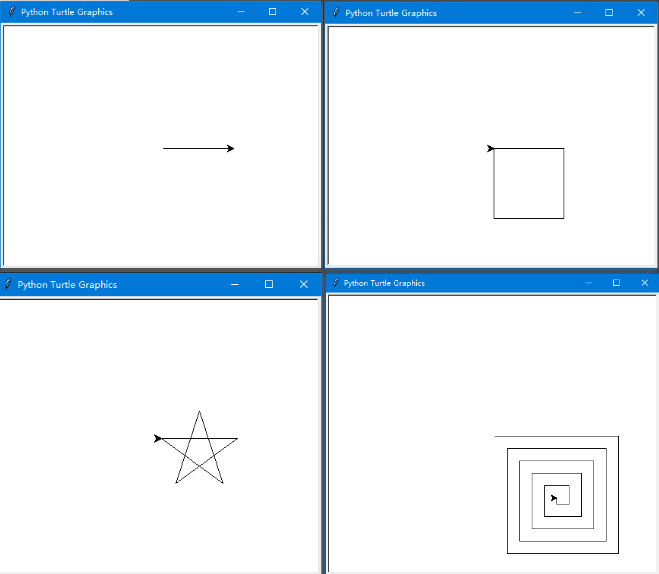
海归作图 turtle module

  • 爬行

    • forward(n)
    • backward(n)
  • 转向
    • left(a)
    • right(a)
  • 抬笔放笔
    • penup()
    • pendown()
  • 笔属性
    • pensize(s)
    • pencolor(c)

  1. # 递归
  2. def listsum(numlist):
  3.     if len(numlist) == 1:
  4.         return numlist[0]
  5.     else:
  6.         return numlist[0]+listsum(numlist[1:])
  8. def toStr(n, base):
  9.     convertString = "0123456789ABCDEF"
  10.     if n < base:
  11.         return convertString[n]
  12.     else:
  13.         return toStr(n//base,base)+convertString[n % base]
  15. import turtle
  17. def draw_forward():
  18.     """前向示例"""
  19.     t=turtle.Turtle()
  20.     # 作图开始
  21.     t.forward(100) #指挥海归作图
  22.     # 作图结束
  23.     turtle.done()
  25. def draw_square():
  26.     """绘制正方形"""
  27.     t=turtle.Turtle()
  28.     for i in range (4):
  29.         t.forward(100)
  30.         t.right(90)
  32.     turtle.done()
  34. def draw_pentagram():
  35.     """绘制五角星"""
  36.     t=turtle.Turtle()
  37.     for i in range (5):
  38.         t.forward(100)
  39.         t.right(144)
  41.     turtle.done()
  43. def drawSpiral(t,linelen):
  44.     """绘制螺旋"""
  45.     if linelen>0:
  46.         t.forward(linelen)
  47.         t.right(90)
  48.         drawSpiral(t,linelen-10)
  50. if __name__ == "__main__":
  51.     #draw_forward()
  52.     #draw_square()
  53.     #draw_pentagram()
  55.     t=turtle.Turtle()
  56.     drawSpiral(t,200)
  57.     turtle.done()

分形树：自相似递归图形

  1. import turtle
  2. def tree(t,branch_len):
  3.     if branch_len>5:
  4.         t.forward(branch_len)
  5.         t.right(20)
  6.         tree(t,branch_len-15)
  7.         t.left(40)
  8.         tree(t,branch_len-15)
  9.         t.right(20)
  10.         t.backward(branch_len)
  12. if __name__ == "__main__":
  13.     t=turtle.Turtle()
  14.     t.left(90)
  15.     t.penup()
  16.     t.backward(100)
  17.     t.pendown()
  18.     t.pencolor("green")
  19.     t.pensize(2)
  20.     tree(t,75)
  21.     t.hideturtle()
  22.     turtle.done()

谢尔宾斯基三角

作图思路

  • degree=n

    • 三角形是由3个degree=n-1的三角形按照品字形拼叠而成
    • 这个3个degree=n-1的三角形边长均为degree=n的三角形的一半(规模减小)
  • degree=0
    • 等边三角形，这是递归的基本结束条件

代码

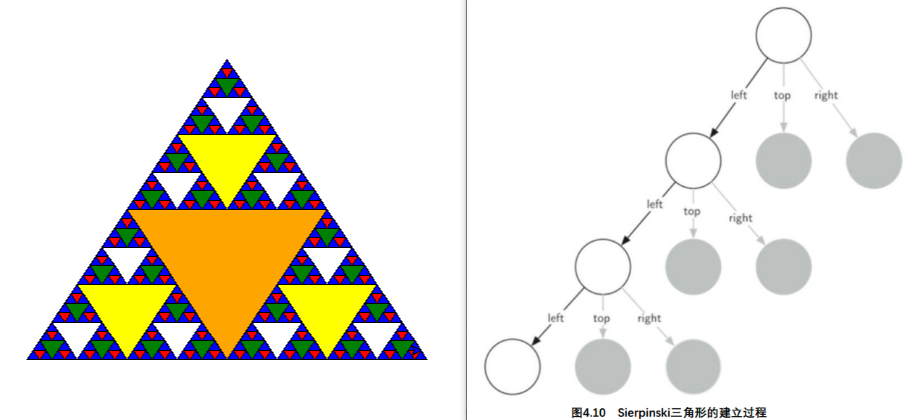
  1. import turtle
  2. def sierpinski(t, degree, points):
  3.     """谢尔宾斯基三角"""
  4.     colormap = ['blue', 'red', 'green', 'white', 'yellow', 'orange']
  5.     drawTriangle(t, points, colormap[degree])
  6.     if degree > 0:
  7.         # 左边三角形
  8.         sierpinski(t, degree-1,
  9.                    {
  10.                        'left': points['left'],
  11.                        'top': getMid(points['left'], points['top']),
  12.                        'right': getMid(points['left'], points['right'])
  13.                    }
  14.                    )
  15.         # 顶部三角形
  16.         sierpinski(t, degree-1,
  17.                    {
  18.                        'left': getMid(points['left'], points['top']),
  19.                        'top': points['top'],
  20.                        'right': getMid(points['top'], points['right'])
  21.                    }
  22.                    )
  23.         # 右边三角形
  24.         sierpinski(t, degree-1,
  25.                    {
  26.                        'left': getMid(points['left'], points['right']),
  27.                        'top': getMid(points['top'], points['right']),
  28.                        'right': points['right']
  29.                    }
  30.                    )
  32. def drawTriangle(t, points, color):
  33.     t.fillcolor(color)
  34.     t.penup()
  35.     t.goto(points['top'])
  36.     t.pendown()
  37.     t.begin_fill()
  38.     t.goto(points['left'])
  39.     t.goto(points['right'])
  40.     t.goto(points['top'])
  41.     t.end_fill()
  43. def getMid(p1, p2):
  44.     return ((p1[0]+p2[0])/2, (p1[1]+p2[1])/2)
  46. if __name__ == "__main__":
  47.     t = turtle.Turtle()
  48.     points = dict(
  49.         left=(-200, -100),
  50.         top=(0, 200),
  51.         right=(200, -100)
  52.     )
  53.     sierpinski(t, 5, points)
  54.     turtle.done()

汉诺塔

描述

  • 汉诺塔问题是法国数学家爱德华·卢卡斯于1883年发现的。他受到一个关于印度教寺庙的传说的启发，故事中这一问题交由年轻僧侣们解决。最开始，僧侣们得到三根杆子， 64个金圆盘堆叠在其中一根上, 每个圆盘比其下的小一点。僧侣们的任务是将64个圆盘从一根杆上转移到另一根杆上，但有两项重要的限制,一是他们一次只能移动一个圆盘,一是不能将大圆盘放在小圆盘之上。僧侣们日以继夜地工作，每秒移动一个圆盘。 传说中，当工作完成之时寺庙就会崩塌, 世界则将不复存在。
  • 传说很有趣，但也不用为世界末日将要到来而担心。毫无差错地完成这项工作需要264-1=18,446,774,073,709,551,615次移动。如果每秒移动一次则需要584,942,417,335（五千亿）年!显然实际上会更长

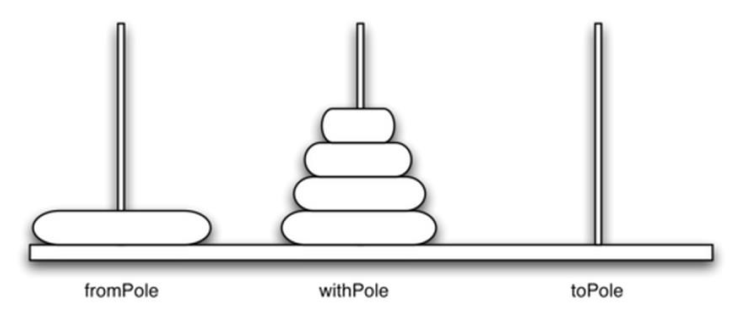
递归思路

  • 将盘片塔从开始柱，经由中间柱，移动到目标柱：

    1. 首先将上层N-1个盘片的盘片塔，从开始柱，经由目标柱，移动到中间柱
    2. 然后将第N个（最大）盘片，从开始柱，移动到目标柱
    3. 最后将放置在中间柱的N-1个盘片的盘片塔，经由开始柱，移动到目标柱
  • 基本结束条件，即最小规模问题：一个盘片的移动问题

代码实现

  1. def moveTower(height,fromPole,withPole,toPole):
  2.     if height>=1:
  3.         moveTower(height-1,fromPole,toPole,withPole)
  4.         moveDisk(height,fromPole,toPole)
  5.         moveTower(height-1,withPole,fromPole,toPole)
  7. def moveDisk(disk,fromPole,toPole):
  8.     print(f"Moving disk[{disk}] from {fromPole} to {toPole}")
  10. if __name__ == "__main__":
  11.     moveTower(3,"#1","#2","#3")
  13. >>>
  14. Moving disk[1] from #1 to #3
  15. Moving disk[2] from #1 to #2
  16. Moving disk[1] from #3 to #2
  17. Moving disk[3] from #1 to #3
  18. Moving disk[1] from #2 to #1
  19. Moving disk[2] from #2 to #3
  20. Moving disk[1] from #1 to #3

探索迷宫

原文

  • 古希腊迷宫

    • 克里特岛米诺斯王
    • 牛头人身怪物米诺陶洛斯
  • 圆明园 万花阵

算法思路

  • 步骤

    • 在初始位置尝试向北走一步，以此为开始递归程序。
    • 北面走不通的情况下则向南尝试，其后开始递归。
    • 南面走不通的情况下则向西尝试，其后开始递归。
    • 如果北面、南面、西面都走不通，则从东面开始并递归程序
    • 如果四个方向都走不出，则被困在迷宫中，以失败告终

  • 四种基本情况需要考虑:

    1、 海龟碰到“墙壁”，方格被占用无法通行。

    2、 海龟发现表示此方格已访问过，为避免陷入循环不在此位置继续寻找。

    3、 海龟碰到位于边缘的通道，即找到迷宫出口。

    4、 海龟在四个方向上探索都失败。

  • 递归归纳：

    • 海龟碰到“墙壁”方格，递归调用结束，返回失败
    • 海龟碰到“面包屑”方格，表示此方格已访问过，递归调用结束，返回失败
    • 海龟碰到“出口”方格，即“位于边缘的通道”方格，递归调用结束，返回成功！
    • 海龟在四个方向上的探索都失败，递归调用结束，返回失败

代码实现

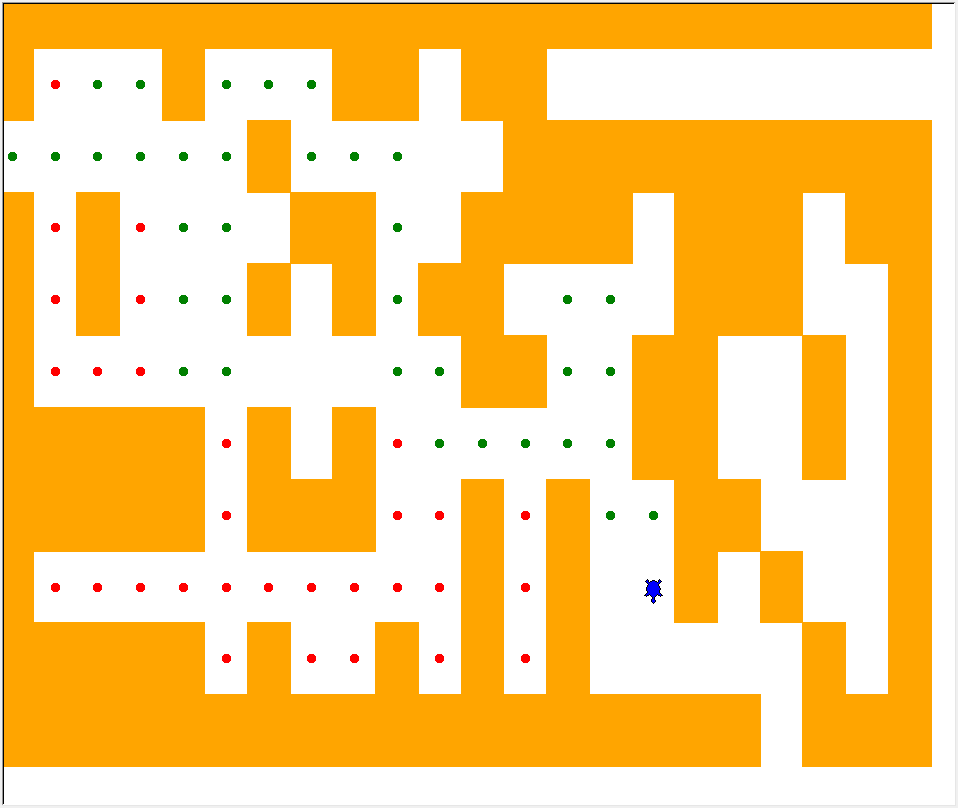
  • 代码
  1. import turtle
  2. PART_OF_PATH = 'O'
  3. TRIED = '.'
  4. OBSTACLE = '+'
  5. DEAD_END = '-'
  6. class Maze:
  7.     def __init__(self):
  8.         self.mazelist = [
  9.             ['+', '+', '+', '+', '+', '+', '+', '+', '+', '+', '+','+', '+', '+', '+', '+', '+', '+', '+', '+', '+', '+'],
  10.             ['+', ' ', ' ', ' ', '+', ' ', ' ', ' ', '+', '+', ' ','+', '+', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '],
  11.             [' ', ' ', ' ', ' ', ' ', ' ', '+', ' ', ' ', ' ', ' ',' ', '+', '+', '+', '+', '+', '+', '+', '+', '+', '+'],
  12.             ['+', ' ', '+', ' ', ' ', ' ', ' ', '+', '+', ' ', ' ','+', '+', '+', '+', ' ', '+', '+', '+', ' ', '+', '+'],
  13.             ['+', ' ', '+', ' ', ' ', ' ', '+', ' ', '+', ' ', '+','+', ' ', ' ', ' ', ' ', '+', '+', '+', ' ', ' ', '+'],
  14.             ['+', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ','+', '+', ' ', ' ', '+', '+', ' ', ' ', '+', ' ', '+'],
  15.             ['+', '+', '+', '+', '+', ' ', '+', ' ', '+', ' ', ' ',' ', ' ', ' ', ' ', '+', '+', ' ', ' ', '+', ' ', '+'],
  16.             ['+', '+', '+', '+', '+', ' ', '+', '+', '+', ' ', ' ','+', ' ', '+', ' ', ' ', '+', '+', ' ', ' ', ' ', '+'],
  17.             ['+', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ','+', ' ', '+', ' ', 'S', '+', ' ', '+', ' ', ' ', '+'],
  18.             ['+', '+', '+', '+', '+', ' ', '+', ' ', ' ', '+', ' ','+', ' ', '+', ' ', ' ', ' ', ' ', ' ', '+', ' ', '+'],
  19.             ['+', '+', '+', '+', '+', '+', '+', '+', '+', '+', '+','+', '+', '+', '+', '+', '+', '+', ' ', '+', '+', '+']
  20.         ]
  21.         self.startRow=8
  22.         self.startCol=15
  23.         self.rowsInMaze =len(self.mazelist)
  24.         self.columnsInMaze =len(self.mazelist[0])
  25.         self.xTranslate=-self.columnsInMaze/2
  26.         self.yTranslate=self.rowsInMaze/2
  27.         self.t = turtle.Turtle()
  28.         self.t.shape('turtle')
  29.         self.wn = turtle.Screen()
  30.         self.wn.setworldcoordinates(-(self.columnsInMaze-1)/2-.5,
  31.                                     -(self.rowsInMaze-1)/2-.5,
  32.                                     (self.columnsInMaze-1)/2+.5,
  33.                                     (self.rowsInMaze-1)/2+.5)
  35.     def drawMaze(self):
  36.         self.t.speed(10)
  37.         self.wn.tracer(0)
  38.         for y in range(self.rowsInMaze):
  39.             for x in range(self.columnsInMaze):
  40.                 if self.mazelist[y][x] == OBSTACLE:
  41.                     self.drawCenteredBox(x+self.xTranslate,-y+self.yTranslate,'orange')
  42.         self.t.color('black')
  43.         self.t.fillcolor('blue')
  44.         self.wn.update()
  45.         self.wn.tracer(1)
  47.     def drawCenteredBox(self,x,y,color):
  48.         self.t.up()
  49.         self.t.goto(x-.5,y-.5)
  50.         self.t.color(color)
  51.         self.t.fillcolor(color)
  52.         self.t.setheading(90)
  53.         self.t.down()
  54.         self.t.begin_fill()
  55.         for i in range(4):
  56.             self.t.forward(1)
  57.             self.t.right(90)
  58.         self.t.end_fill()
  60.     def moveTurtle(self,x,y):
  61.         self.t.up()
  62.         self.t.setheading(self.t.towards(x+self.xTranslate,-y+self.yTranslate))
  63.         self.t.goto(x+self.xTranslate,-y+self.yTranslate)
  65.     def dropBreadcrumb(self,color):
  66.         self.t.dot(10,color)
  68.     def updatePosition(self,row,col,val=None):
  69.         if val:
  70.             self.mazelist[row][col] = val
  71.         self.moveTurtle(col,row)
  73.         if val == PART_OF_PATH:
  74.             color = 'green'
  75.         elif val == OBSTACLE:
  76.             color = 'red'
  77.         elif val == TRIED:
  78.             color = 'black'
  79.         elif val == DEAD_END:
  80.             color = 'red'
  81.         else:
  82.             color = None
  84.         if color:
  85.             self.dropBreadcrumb(color)
  87.     def isExit(self,row,col):
  88.         return (row == 0 or
  89.                 row == self.rowsInMaze-1 or
  90.                 col == 0 or
  91.                 col == self.columnsInMaze-1 )
  93.     def __getitem__(self,idx):
  94.         return self.mazelist[idx] 
  96. def searchFrom(maze, startRow, startColumn):
  97.     # 1.碰到墙壁，返回失败
  98.     maze.updatePosition(startRow, startColumn)
  99.     if maze[startRow][startColumn] == OBSTACLE :
  100.         return False
  102.     # 2. 碰到面包屑，或者死胡同，返回失败
  103.     if maze[startRow][startColumn] == TRIED or maze[startRow][startColumn] == DEAD_END:
  104.         return False
  106.     # 3. 碰到出口，返回成功
  107.     if maze.isExit(startRow,startColumn):
  108.         maze.updatePosition(startRow, startColumn, PART_OF_PATH)
  109.         return True
  111.     # 4.洒下面包屑，继续探索
  112.     maze.updatePosition(startRow, startColumn, TRIED)
  114.     # 向北南西东4个方向依次探索，or操作符具有短路效应
  115.     found = searchFrom(maze, startRow-1, startColumn) or \
  116.             searchFrom(maze, startRow+1, startColumn) or \
  117.             searchFrom(maze, startRow, startColumn-1) or \
  118.             searchFrom(maze, startRow, startColumn+1)
  120.     # 如果探索成功，标记当前点，失败则标记为“死胡同”
  121.     if found:
  122.         maze.updatePosition(startRow, startColumn, PART_OF_PATH)
  123.     else:
  124.         maze.updatePosition(startRow, startColumn, DEAD_END)
  125.     return found
  127. if __name__ == "__main__":
  128.     myMaze = Maze()
  129.     myMaze.drawMaze()
  130.     myMaze.updatePosition(myMaze.startRow,myMaze.startCol)
  131.     searchFrom(myMaze, myMaze.startRow, myMaze.startCol)
  132.     turtle.done()

【数据结构与算法Python版学习笔记】递归(Recursion)——定义及应用：分形树、谢尔宾斯基三角、汉诺塔、迷宫的更多相关文章

  1. python 使用turtule绘制递归图形（螺旋、二叉树、谢尔宾斯基三角形）

    插图工具使用Python内置的turtle模块,为什么叫这个turtle乌龟这个名字呢,可以这样理解,创建一个乌龟,乌龟能前进.后退.左转.右转,乌龟的尾巴朝下,它移动时就会画一条线.并且为了增加乌龟 ...

  2. 【数据结构与算法Python版学习笔记】目录索引

    引言 算法分析 基本数据结构 概览 栈 stack 队列 Queue 双端队列 Deque 列表 List,链表实现 递归(Recursion) 定义及应用:分形树.谢尔宾斯基三角.汉诺塔.迷宫 优化 ...

  3. 【数据结构与算法Python版学习笔记】引言

    学习来源 北京大学-数据结构与算法Python版 目标 了解计算机科学.程序设计和问题解决的基本概念 计算机科学是对问题本身.问题的解决.以及问题求解过程中得出的解决方案的研究.面对一 个特定问题,计 ...

  4. 【数据结构与算法Python版学习笔记】树——相关术语、定义、实现方法

    概念 一种基本的"非线性"数据结构--树 根 枝 叶 广泛应用于计算机科学的多个领域 操作系统 图形学 数据库 计算机网络 特征 第一个属性是层次性,即树是按层级构建的,越笼统就越 ...

  5. 【数据结构与算法Python版学习笔记】递归(Recursion)——优化问题与策略

    分治策略:解决问题的典型策略,分而治之 将问题分为若干更小规模的部分 通过解决每一个小规模部分问题,并将结果汇总得到原问题的解 递归算法与分治策略 递归三定律 体现了分支策略 应用相当广泛 排序 查找 ...

  6. 【数据结构与算法Python版学习笔记】查找与排序——散列、散列函数、区块链

    散列 Hasing 前言 如果数据项之间是按照大小排好序的话,就可以利用二分查找来降低算法复杂度. 现在我们进一步来构造一个新的数据结构, 能使得查找算法的复杂度降到O(1), 这种概念称为" ...

  7. 【数据结构与算法Python版学习笔记】算法分析

    什么是算法分析 算法是问题解决的通用的分步的指令的聚合 算法分析主要就是从计算资源的消耗的角度来评判和比较算法. 计算资源指标 存储空间或内存 执行时间 影响算法运行时间的其他因素 分为最好.最差和平 ...

  8. 【数据结构与算法Python版学习笔记】基本数据结构——列表 List，链表实现

    无序表链表 定义 一种数据项按照相对位置存放的数据集 抽象数据类型无序列表 UnorderedList 方法 list() 创建一个新的空列表.它不需要参数,而返回一个空列表. add(item) 将 ...

  9. 【数据结构与算法Python版学习笔记】图——骑士周游问题 深度优先搜索

    骑士周游问题 概念 在一个国际象棋棋盘上, 一个棋子"马"(骑士) , 按照"马走日"的规则, 从一个格子出发, 要走遍所有棋盘格恰好一次.把一个这样的走棋序列 ...

随机推荐

  1. github上使用C语言实现的线程池

    网上介绍线程池的知识很多,但是在代码实现上介绍的又不是那么多.而且给人的一种感觉就是:你的这种实现是正规的方式还是你自己的实现? 如果有这么个疑问,且想找一个靠谱的代码拿来使用,那么这个项目是个不错的 ...

  2. vue页面跳转以及传参和取参

    vue中this.$router.push()路由传值和获取的两种常见方法 1.路由传值   this.$router.push() (1) 想要导航到不同的URL,使用router.push()方法 ...

  3. Excel怎么把两个单元格中的文字合并到一个单元格中

    使用&符号,可以将字符串和单元格中的内容拼接起来

  4. 'Specifying a namespace in include() without providing an app_name '报错解决

    需要在每个ap下面的url.py 加入一个指定app的名字 比如  user  app  下的 url.py  文件加入: urlpatterns = []app_name = "user& ...

  5. 关于buildroot移植的思考

    buildroot是一个成熟的SDK框架,基于它有了openwrt. 曾经有一个项目,需要将原有的OpenWrt SDK改造,并且将软件框架重新定义.尝试精简原来的OpenWrt,并且删除所有的软件包 ...

  6. PHP的OpenSSL加密扩展学习（三）：证书操作

    关于对称和非对称的加密操作,我们已经学习完两篇文章的内容了,接下来,我们就继续学习关于证书的生成. 生成 CSR 证书签名请求 CSR 是用于生成证书的签名请求,在 CSR 中,我们需要一些 dn 信 ...

  7. Centos 7 设置 SFTP

    近期要给服务器设置一个SFTP用户,可以上传删除修改的SFTP,但是禁止该用户SSH登录.这里记录下来 先升级 来源: https://blog.csdn.net/fenglailea/article ...

  8. sqlalchemy 查询结果转json个人解决方案

    参考了网上很多资料,自己搞了一个适合的 在model 内增加一个函数: class User(db.Model): __tablename__ = 'user' userid = db.Column( ...

  9. P2012-拯救世界2【EGF】

    正题 题目链接:https://www.luogu.com.cn/problem/P2012 题目大意 \(12\)种东西排列成长度为\(n\)的序列,要求前四种出现奇数次,后四种出现偶数次,求方案. ...

  10. P4234-最小差值生成树【LCT】

    正题 题目链接:https://www.luogu.com.cn/problem/P4234 题目大意 给出\(n\)个点\(m\)条边的一张图.求一棵生成树使得最大边权减去最小边权最小. \(1\l ...