Radix Sorts
基数排序
Strings In Java
Char Data Type
C 语言中的字符数据类型占一个字节(8 比特),最多只能表示 256 个字符。支持 7 位的标准 ASCII(American Standard Code for Information Interchange,美国标准信息交换编码),最高位用于奇偶校验。或是拓展的 ASCII,最高位用来确定附加的 128 个特殊的字符。
标准 ASCII 的十六进制转换表
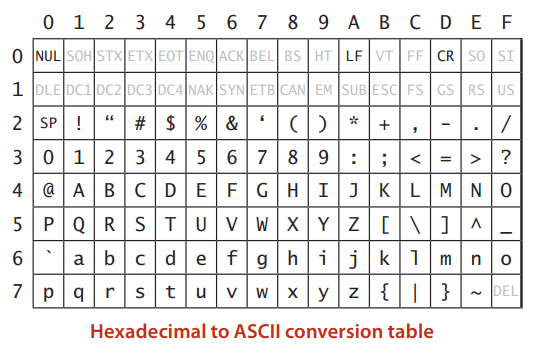
Java 中的字符数据类型占两个字节,支持 16 位的 Unicode 编码。
String Data Type
字符串就是一些字符组成的序列,不是原生的数据类型,在 Java 中是不可变(immutable)的对象,实现了一些方便的方法:
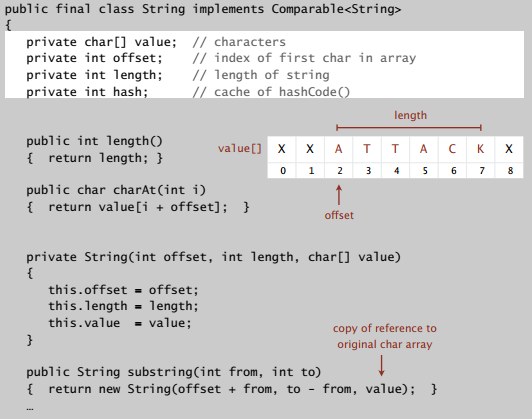
表示字符串的字符数组是不可变的,获取的子字符串其实也保存在这个字符数组里,所以在常数时间内就能完成。但是连接两个字符串的时候,就要新建字符串对象,需要正比于字符串长度的时间。
StringBuilder Data Type
StringBuilder 的字符序列是可变的(mutable),内部实现用的是可变长的字符数组,所以连接字符串的操作几乎能在常数时间完成。但是相应的,获取子字符串的操作需要正比于字符串长度的时间。
所以在实际的使用中,我们要根据不同的需求,选择合适的对象来表示字符串。
Key-indexed counting
基于比较的排序至少需要 \(NlgN\) 次的比较,先介绍一种不是基于比较的,适用于排序的键是小整数的情况,它也是下面其它字符串排序算法的基础,称作:键索引计数法。
设想有个数组 a = {d, a, c, f, f, b, d, b, f, b, e, a} 要排序,知道总共有 6 个不同的字母,要先统计它们出现的频数。
int R = 6;
int N = a.length;
int[] count = new int[R + 1];
for (int i = 0; i < N; i++)
count[a[i] - 'a' + 1]++;
字母 a 的键为 0 (a[i] - 'a'),出现的次数在 count 数组中的索引为键值加一。

遍历一遍 count 数组:
for (int i = 0; i < R; i++)
count[i + 1] += count[i];
现在 count 数组中保存的即对应字母在排好序的数组中开始的索引值,像两个 d 应该放在 a[6] 和 a[7]。
char[] aux = new char[N];
for (int i = 0; i < N; i++)
aux[count[a[i] - 'a']++] = a[i];
辅助数组 aux 借助 count 数组找到了每个 a[i] 的位置。注意 count 数组在这一步中还会改变,每次要加一,下次相同的 a[i] 就会放在下一个位置。所以这个算法也是稳定的(stable),相同元素间的相对顺序不会改变。

最后把 aux 数组一个个赋值回原数组,即完成了排序。
键索引计数法排序只需要几个一重循环,不需要比较,只要 R 在 N 的一个常数因子范围内,它就是一个线性时间级别的排序方法。
LSD Radix Sort
低位优先(Least Significant digit first)的基数排序,可以对等长的字符串进行排序。这样的应用挺常见,像电话号码,车牌号等等。你需要做的是从右到左,分别对每个位置的字符进行基数排序,像下面的例图那样:
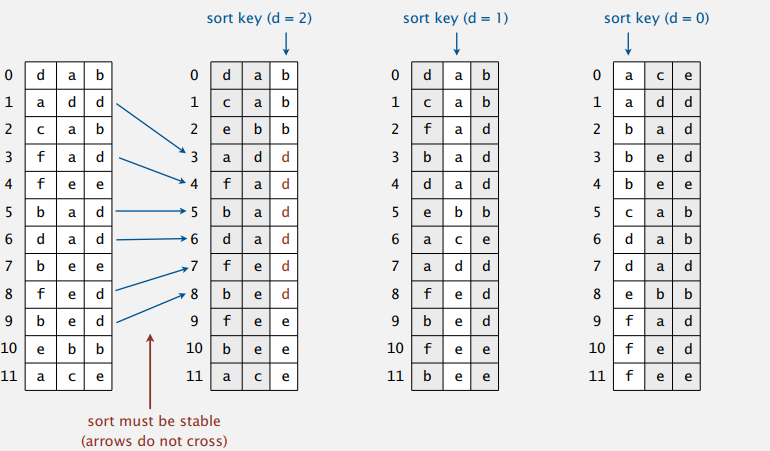
因为基数排序是稳定的,相同键之间的相对顺序不会改变,所以第 i + 1 次排完之后,i + 1 位有相同键的字符串的前面 i 位间的相对顺序是不会变的,仍然有序。
LSD: Java Implementation
public class LSD {
// fixed-length W strings
public static void sort(String[] a, int W) {
int R = 256; // radix R
int N = a.length;
String[] aux = new String[N];
// do key-indexed couting
// for each digit from right to left
for (int d = W - 1; d >= 0; d--) {
int[] count = new int[R + 1];
// key-indexed counting
for (int i = 0; i < N; i++)
count[a[i].charAt(d) + 1]++;
for (int r = 0; r < R; r++)
count[r + 1] += count[r];
for (int i = 0; i < N; i++)
aux[count[a[i].charAt(d)]++] = a[i];
for (int i = 0; i < N; i++)
a[i] = aux[i];
}
}
}
对于典型的应用,R(基数)远小于 N(总数),对定长(W)的字符串排序的时间是 \(MN\) 级别。
MSD Radix Sort
高位优先(Most Significant Digit First)的基数排序,能对长度不同的字符串进行排序。对最高位的字符使用基数排序,然后再递归地对子字符串们使用基数排序:
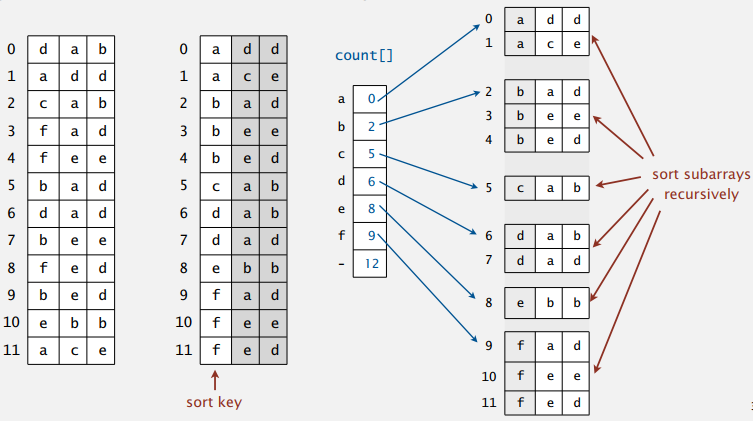
这些字符串可以不是定长的,我们要约定一下的字符串的末尾。这里用私有方法 charAt() 在字符串的末尾加个 -1,这样下一轮的基数排序中它也不会改变位置。C 语言中字符串以 ‘\0’ 结尾,需要注意对代码做些调整。
private static int charAt(String s, int d) {
if (d < s.length) return s.charAt(d);
else return -1;
}
MSD: Java Implementation
于是相当于现在多了个键 -1,所以 conut 数组的大小为 R + 2。
public static void sort(String[] a) {
aux = new String[a.length];
sort(a, aux, 0, a.length - 1, 0);
}
private static void sort(String[] a, String[] aux, int lo, int hi, int d) {
if (hi <= lo) return;
int[] count = new int[R + 2];
for (int i = lo; i <= hi; i++)
count[charAt(a[i], d) + 2]++;
for (int r = 0; r < R + 1; r++)
count[r + 1] += count[r];
for (int i = lo; i <= h; i++)
aux[count[charAt(a[i], d) + 1]++] = a[i];
for (int i = lo; i <= hi; i++)
a[i] = aux[i -lo];
// sort R subarrays recursively
for (int r = 0; r < R; r++)
sort(a, aux, lo + count[r], lo + count[r + 1] - 1, d + 1);
}
用于回写的辅助数组 aux 可以重复使用,但是每次基数排序都需要新的 count[R + 2],不仅需要空间,而且默认的初始化也需要时间。于是,类似的,对于小型子数组,我们使用插入排序来改进算法。
public static void sort(String[] a, int lo, int hi, int d) {
for (int i = lo; i <= hi; i++)
for (int j = i; j > lo && less(a[j], a[j - 1], d); j--)
exch(a, j, j -1);
}
private static boolean less(String v, String w, int d) {
return v.substring(d).compareTo(w.substring(d)) < 0;
}
MSD 算法的性能取决于输入的数据,最坏的情况的下需要检查所有的字符,和 LSD 一样是线性时间级别。

3-way Radix Quicksort
三向字符串快速排序算法结合了 MSD 和快排,改进了快速排序处理字符串时的性能。当两个字符串有很长的相同前缀时,不需要重复扫描很多字符,也不像 MSD 因为辅助数组而需要很多额外空间。
具体来说,算法每次根据第一个字符串的首字母将数组三向切分成小于,等于和大于首字母的三个子数组,然后再递归地对这些子数组三向切分。其中,首字母相等的子数组用第一个字符串的第二个字母来三向切分,因为首字母都一样,同时也避免了原来快排的重复扫描。例图:
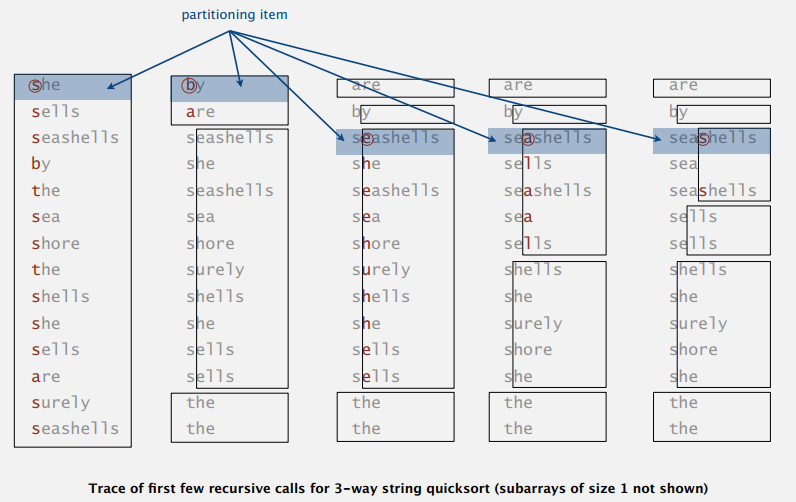
3-way String Quicksort: Java Implementation
private static void sort(String[] a) {
sort(a, 0, a.length - 1, 0);
}
private static void sort(String[] a, int lo, int hi, int d) {
if (hi <= lo) return;
int lt = lo, gt = hi;
int v = charAt(a[lo], d); // 约定字符串末尾返回 -1
int i = lo + 1;
while (i <= gt) {
int t = charAt(a[i], d);
if (t < v) exch(a, lt++, i++);
else if (t > v) exch(a, i, gt--);
else i++;
}
sort(a, lo, lt - 1, d);
if (v >=0) sort(a, lt, gt, d + 1); // 用第二个字母三向切分
sort(a, gt + 1, hi, d);
}
Suffix Arrays
后缀数组包括字符串的所有后缀,有很多应用,比如说可以用于关键字查找,最长重复子字符串等。
因为 Java 中子字符串共享原来的字符数组,所以构建输入字符串的后缀数组只需要线性级别的时间和空间。
public static String[] suffixes(String s) {
int N = s.length();
String[] suffixes = new String[N];
for (int i = 0; i < N; i++)
suffixes[i] = s.substring(i, N);
return suffixes;
}
对后缀数组进行排序,就能把相同的字符串安排在一起,查找关键字也就快了很多。

最长重复子字符串也差不多。

LRS: Java Implementation
public String lrs(String s) {
int N = s.length();
String[] suffixes = new String[N];
for (int i = 0; i < N; i++)
suffixes[i] =s.substring(i, N);
Arrays.sort(suffixes);
tring lrs = "";
for (int i = 0; i < N - 1; i++) {
// compute longest common prefix
// between adjacent suffixes insorted order
int len = lcp(suffixes[i], suffixes[i + 1]);
if (len > lrs.length())
lrs = suffixes[i].substring(0, len);
}
return lrs;
}
不过,最坏情况下,它可能达到平方级别的复杂度。

输入的字符串重复时,需要进行很多次比较才能完成排序。于是乎我们来了解一下 Manber-Myer MSD 算法。

它和普通的 MSD 从左到右一位位排序不同,每次排好的位数是倍增的,像上面排好了前四位,下一轮就能按前八位排好后缀数组。大概的原理,举例来说看字符串 0 和字符串 9,它们有相同的前四位,前者的后四位和字符串 4 的前四位一样,后者的后四位和字符串 13 的前四位一样。而按前四位排序,字符串 13 在字符串 4前面,所以下一次按八位排,字符串 0 应该排在字符串 9 的前面。

大概是这么个过程吧,了解一下,具体实现的细节没提。
Radix Sorts的更多相关文章
- 基数排序(radix sort)
#include<iostream> #include<ctime> #include <stdio.h> #include<cstring> #inc ...
- [Algorithms] Radix Sort
Radix sort is another linear time sorting algorithm. It sorts (using another sorting subroutine) the ...
- Java字节数组转按radix进制输出
代码如下: public class Main_bytesToStr { public static void main(String[] args) throws IOException { // ...
- 1010. Radix (25)(未完成)
Given a pair of positive integers, for example, 6 and 110, can this equation 6 = 110 be true? The an ...
- Trie / Radix Tree / Suffix Tree
Trie (字典树) "A", "to", "tea", "ted", "ten", "i ...
- Uva 110 - Meta-Loopless Sorts(!循环,回溯!)
题目来源:https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=3&pa ...
- PAT 解题报告 1010. Radix (25)
1010. Radix (25) Given a pair of positive integers, for example, 6 and 110, can this equation 6 = 11 ...
- Uva110 Meta-Loopless Sorts
Meta-Loopless Sorts Background Sorting holds an important place in computer science. Analyzing and i ...
- 基数树(radix tree)
原文 基数(radix)树 Linux基数树(radix tree)是将指针与long整数键值相关联的机制,它存储有效率,并且可快速查询,用于指针与整数值的映射(如:IDR机制).内存管理等.ID ...
随机推荐
- redis实战笔记(1)-第1章 初识Redis
第1章 初识Redis 注:本书在redis3.0版本的,比如redis3.0以后支持服务端集群.3.0之前只能客户端分片. 本章主要内容 1.Redis与其他软件的相同之处和不同之处 2.Re ...
- 动态生成自定义控件ascx如何给ascx传值
有机会看到有网友在论坛上发出问题: 在网页上的铵钮执行之后,动态加载的用户控件,如果没有处理好,会在子用户控件的铵钮被执行时抛弃.因此我们需要着重需要处理的关键点.同相子用户控件在动态加载之后,它的状 ...
- A记录,CNAME,MX记录,TTL
A记录 A记录是用来指定主机名(或域名)对应的IP地址记录.用户可以将该域名下的网站服务器指向到自己的web server上.同时也可以设置您域名的二级域名. MX记录 MX记录邮件路由记录,用户可以 ...
- Orchard源码:热启动
概述 IIS线程池中的线程数量是有限制的.当有多个长时间请求时,可能会耗尽IIS可用线程.出现503错误.在MVC中.当遇到非CPU操作的长时间请求时,MVC提供了异步方法来解决这个问题. 例:利用a ...
- C#可选参数、命名参数、参数数组
学习了C#4.0的新特性:可选参数.命名参数.参数数组. 1.可选参数,是指给方法的特定参数指定默认值,在调用方法时可以省略掉这些参数. 但要注意: (1)可选参数不能为参数列表的第1个参数,必须位于 ...
- 三、hbase JavaAPI
hbase是Java编写的,当然也提供了Java的API来操作hbase. 如果你是使用虚拟机来安装配置hbase那么你需要配置一下hostname,不然JavaAPI访问虚拟机的时候会无法连接,请参 ...
- 最新的dubbo和zookeeper整合的问题
最新的dubbo和zookeeper整合的问题 生活本不易,流人遂自安 博主最新在做小项目练手,在进行dubbo和zookeeper整合的时候遇到了一些问题,在这里这些问题做个小总结吧. 首先需要说明 ...
- Maven环境的搭建
1.本地仓库和apache-mavenbin.zip的下载与解压 <1.apache-mavenbin.zip下载网址 http://maven.apache.org/download.cgi ...
- 关于springmvc中常用的注解,自己也整理一下
1.@Controller 在springMVC中@controller主要用在控制层的类上,之前只知道用注解开发的时候必须加一个@controller ,今天看了别的大佬整理的才知道为什么这么用,控 ...
- Luogu4887 第十四分块(前体)
sto \(lxl\) orz 考虑莫队,每次移动端点,我们都要询问区间内和当前数字异或有 \(k\) 个 \(1\) 的数字个数 询问 \([l,r]\) 可以再次离线,拆成询问 \([1,l-1] ...
