Maths | 为什么点积等价于投影后的乘积

目录

• 1. 复习点积
• 2. 点积的对称性
• 3. 矩阵与变换的关系
• 4. 一维矩阵也是一种线性变换
• 5. 最终解释：为什么是投影

先上结论：

1. \(\boldsymbol v\)和\(\boldsymbol w\)点积，就是向量乘法\(\boldsymbol v × \boldsymbol w^T\)；
2. \(\boldsymbol w\)象征着一个降维变换矩阵，因此该矩阵乘法本质上是一个\(\boldsymbol v\)降维的过程；
3. 该降维变换在几何上正是投影过程。

综上，点积的几何意义就是投影相乘。

摘自《Essence of linear algebra》系列视频，非常精彩。B站上有全集～
要理解这一点，需要线性代数基础，要理解矩阵和变换之间的关系。

1. 复习点积

我们所学的向量点积是这样的：

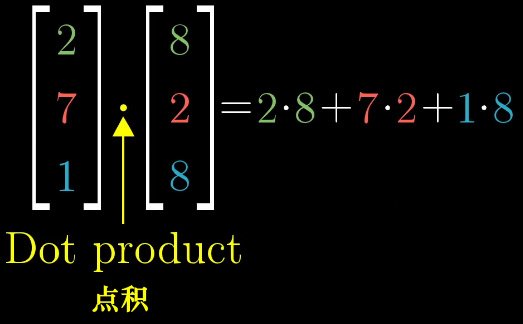
其几何解释为：向量\(\boldsymbol w\)在向量\(\boldsymbol v\)上投影，投影长度和\(|\boldsymbol v|\)相乘。

借助这一几何解释，我们可以直观地理解：

• 向量正交：点积为0
• 投影为反方向：点积为负。

2. 点积的对称性

注意！理解、证明点积的对称性，对我们的证明至关重要！

假设\(\boldsymbol w \bigodot \boldsymbol v\)，对称性的意思是：
无论是\(\boldsymbol v\)在\(\boldsymbol w\)上作投影再乘，还是\(\boldsymbol w\)在\(\boldsymbol v\)上作投影再乘，结果都是一样的。

现在我们证明这一点。

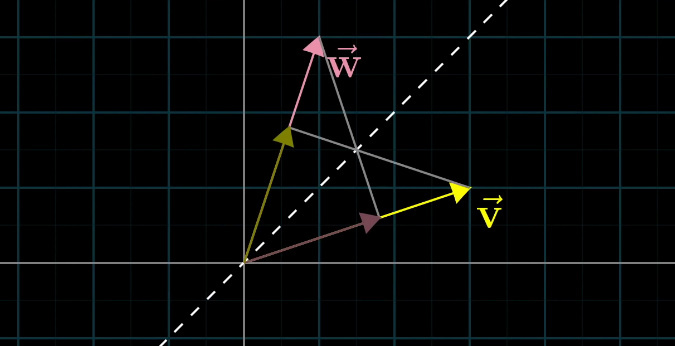
如图，假设二者长度相同，那么对称性显然成立：因为投影长度是一样的。

现在，假设\(\boldsymbol w\)更长。
我们在\(\boldsymbol w\)的方向上取\(\boldsymbol w'\)，使得\(|\boldsymbol w'|\)等于\(|\boldsymbol v|\)。

我们先考虑\(\boldsymbol w' \bigodot \boldsymbol v\)。由于长度相同，对称性是显然的。
而\(\boldsymbol w \bigodot \boldsymbol v\)，和\(\boldsymbol w' \bigodot \boldsymbol v\)只相差常数\(\alpha\)倍：
\[
\alpha = \frac{|\boldsymbol w|}{|\boldsymbol w'|}
\]

3. 矩阵与变换的关系

这一节内容，强烈建议观看推荐视频：《Essence of linear algebra》。

假设现在有矩阵：
\[
\begin{bmatrix}
1 & 0 \\
0 & 1 \\
\end{bmatrix}
\]

这是一个单位阵，作用在任何一个向量\([a,b]\)上，仍然会得到\([a,b]\)。

本质原因是：

• 单位阵第一行\([1,0]\)，代表的是基向量\(\boldsymbol i = [1,0]\)变换后的位置；
• 同理，单位阵第二行\([0,1]\)，代表的是基向量\(\boldsymbol j = [0,1]\)变换后的位置。

显然两个基向量的位置都没发生变化，因此这个变换没有任何变化效果。

而\(a\)是基向量\(\boldsymbol i\)是权重，\(b\)是基向量\(\boldsymbol j\)是权重，\([a,b]\)可以拆解为\(a\boldsymbol i + b\boldsymbol j\)。
由线性性，对任意一个向量\([a,b]\)进行线性变换，等于两个分量分别变换，再相加。
因此任意一个向量与单位阵相乘仍然是其本身。

再举一个例子。设有矩阵：
\[
\begin{bmatrix}
1 & 0 \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\end{bmatrix}
\]

与向量\([a,b]\)相乘，结果为：
\[
[a,b] \begin{bmatrix}
1 & 0 \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\end{bmatrix} = [a+\frac{1}{\sqrt{2}}b,\frac{1}{\sqrt{2}}b]
\]

如果理解了矩阵和变换的含义，理解这个结果就特别简单：

1. 基向量\(\boldsymbol i\)纹丝不动，而基向量\(\boldsymbol j\)变换到了\([\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}]\)。
2. \([a,b]\)可以拆解为\(a\boldsymbol i + b\boldsymbol j\)；
3. 因此\([a,b]\)变换到了\(a[1,0] + b[\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}]\)，结果就是\([a+\frac{1}{\sqrt{2}}b,\frac{1}{\sqrt{2}}b]\)

4. 一维矩阵也是一种线性变换

线性性对我们的证明特别重要，可以解释为什么能分别对基向量作变换，再叠加。

我们都知道，线性性包含齐次性和叠加性。
要证明某一个变换是线性变换，就必须证明该变换具有这两个性质。

我们在这里省略严格的证明，换一个直观的角度予以证明。
线性变换有一个直观的特点：
在二维空间中，如果有一系列等距分布于同一直线上的点：

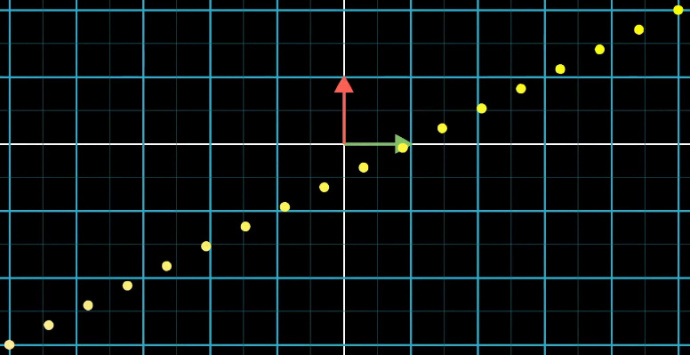
那么线性变换之后，这些点在数轴上仍是等距分布的：

能证明这一点暂时就足够了。
与上一节不同的是，我们现在介绍的是降维变换（2D→1D）。但矩阵和变换的关系还是相同的：
原本二维空间的基向量是[1,0],[0,1]:

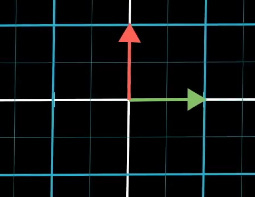
现在变成了数轴上的两个点，也就是两个数（动画更直观，推荐看视频）：

该过程满足保持等距条件。
因为如果把作用向量放大\(\alpha\)倍，实际上就是把两个基向量的权重分别放大\(\alpha\)倍。
被变换作用后再叠加，效果也是放大\(\alpha\)倍。因此等距点仍然是等距点。

这样，我们就粗略说明了该变换是线性变换。

因此我们完全可以认为：
向量[2,1]表征一个从二维到一维的线性变换，将基向量\(\boldsymbol i\)变换至数轴点2，将基向量\(\boldsymbol j\)变换至数轴点1。

5. 最终解释：为什么是投影

现在，我们解释为什么点积可以用投影后的乘积来解释。

我们先来看一个单位向量\(\boldsymbol u\)。

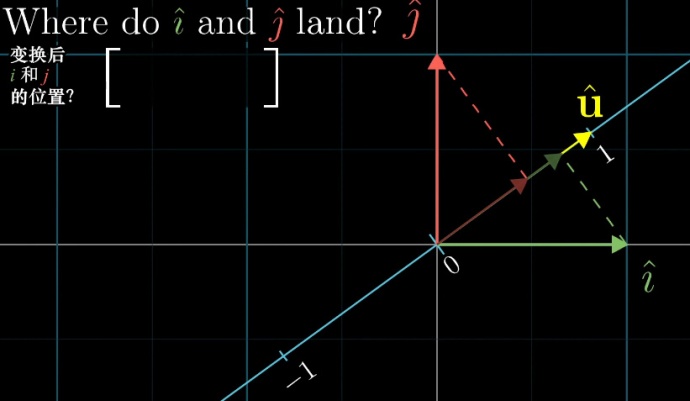
由于是单位向量，因此\(\boldsymbol i = [1,0]\)往\(\boldsymbol u\)上做投影，和\(\boldsymbol u\)往\(\boldsymbol i = [1,0]\)（也即x轴）上做投影，长度是一样的！
也就是说：图中绿色虚线投影得到的投影长度，等于\(\boldsymbol u\)的横坐标\(u_x\)。
同理：图中红色虚线投影得到的投影长度，等于\(\boldsymbol u\)的纵坐标\(u_y\)。

好了。此时假设向量\(\boldsymbol w\)要和单位向量\(\boldsymbol u\)点积。
由上一节推出的性质，基向量在变换\(\boldsymbol u\)下，会分别映射（降维）到点\(u_x\)和\(u_y\)。

设\(\boldsymbol w = [w_x,w_y]\)，那么\(\boldsymbol w\)就会映射到\(w_xu_x+w_yu_y\)。
这就是点积！！！

所以，为什么可以理解为：\(\boldsymbol w\)先投影到\(\boldsymbol u\)上，再做乘积呢？

1. \(\boldsymbol w\)可以拆解为基向量的加权组合。
2. 每一个基向量与变换\(\boldsymbol u\)（先规定为单位向量）作用的结果，又可以分为：
   1. 该变换相当于投影到\(\boldsymbol v\)所在数轴上的一点。
   2. 该点的坐标，正是\(\boldsymbol u\)的横坐标或纵坐标。
   3. 由线性性，基向量分别变换后再相加，等价于向量\(\boldsymbol w\)整体变换的结果。因此我们把两个投影值相加，就得到了最终结果。
3. 因此，从计算过程上看就是：坐标和权重相乘，再相加。这就是点积！
4. 从投影过程上看：\(\boldsymbol w\)在\(\boldsymbol v\)上投影，恰好也可以拆分成两个基向量在\(\boldsymbol v\)投影的叠加。因此点积都是投影！
5. 如果\(\boldsymbol u\)不是单位向量，再乘以其范数即可。这就是完整的点积：投影→相乘！

解释完毕！