基于Python的频谱分析（一）

1、傅里叶变换
  傅里叶变换是信号领域沟通时域和频域的桥梁，在频域里可以更方便的进行一些分析。傅里叶主要针对的是平稳信号的频率特性分析，简单说就是具有一定周期性的信号，因为傅里叶变换采取的是有限取样的方式，所以对于取样长度和取样对象有着一定的要求。

2、基于Python的频谱分析
  将时域信号通过FFT转换为频域信号之后，将其各个频率分量的幅值绘制成图，可以很直观地观察信号的频谱。
   具体分析见代码注释。

import numpy as np#导入一个数据处理模块
import pylab as pl#导入一个绘图模块，matplotlib下的模块

sampling_rate = 8000#采样频率为8000Hz
fft_size = 512 #FFT处理的取样长度
t = np.arange(0, 1.0, 1.0/sampling_rate)#np.arange(起点，终点，间隔)产生1s长的取样时间
x = np.sin(2*np.pi*156.25*t) + 2*np.sin(2*np.pi*234.375*t)#两个正弦波叠加，156.25HZ和234.375HZ
# N点FFT进行精确频谱分析的要求是N个取样点包含整数个取样对象的波形。因此N点FFT能够完美计算频谱对取样对象的要求是n*Fs/N（n*采样频率/FFT长度），
# 因此对8KHZ和512点而言，完美采样对象的周期最小要求是8000/512=15.625HZ,所以156.25的n为10,234.375的n为15。
xs = x[:fft_size]# 从波形数据中取样fft_size个点进行运算
xf = np.fft.rfft(xs)/fft_size# 利用np.fft.rfft()进行FFT计算，rfft()是为了更方便对实数信号进行变换，由公式可知/fft_size为了正确显示波形能量
# rfft函数的返回值是N/2+1个复数，分别表示从0(Hz)到sampling_rate/2(Hz)的分。
#于是可以通过下面的np.linspace计算出返回值中每个下标对应的真正的频率：
freqs = np.linspace(0, sampling_rate/2, fft_size/2+1)
# np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
#在指定的间隔内返回均匀间隔的数字
xfp = 20*np.log10(np.clip(np.abs(xf), 1e-20, 1e100))
#最后我们计算每个频率分量的幅值，并通过 20*np.log10()将其转换为以db单位的值。为了防止0幅值的成分造成log10无法计算，我们调用np.clip对xf的幅值进行上下限处理

#绘图显示结果
pl.figure(figsize=(8,4))
pl.subplot(211)
pl.plot(t[:fft_size], xs)
pl.xlabel(u"Time(S)")
pl.title(u"156.25Hz and 234.375Hz WaveForm And Freq")
pl.subplot(212)
pl.plot(freqs, xfp)
pl.xlabel(u"Freq(Hz)")
pl.subplots_adjust(hspace=0.4)
pl.show()

3、绘图结果显示

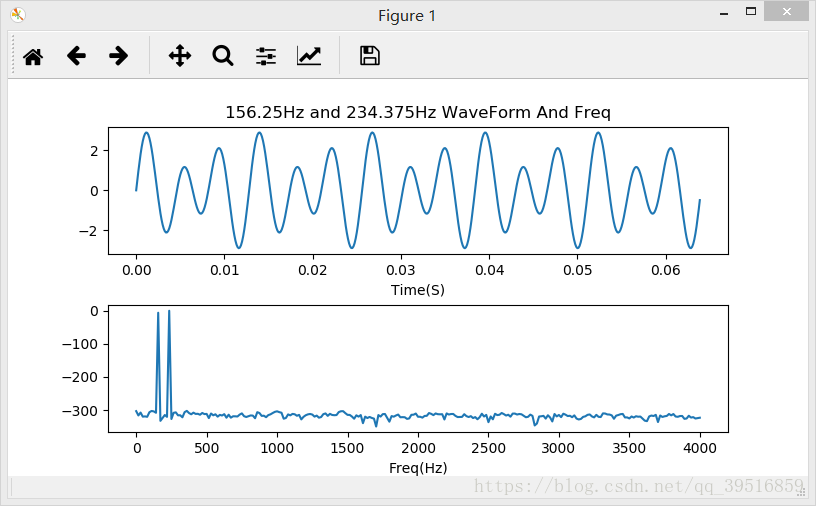
如果你放大其频谱中的两个峰值的部分的话，可以看到其值分别为：

>>>xfp[10]
-6.0205999132796251
>>>xfp[15]
-9.6432746655328714e-16

即156.25Hz的成分为-6dB， 而234.375Hz的成分为0dB，与波形的计算公式中的各个分量的能量(振幅值/2)符合。
---------------------
作者：赵至柔
来源：CSDN
原文：https://blog.csdn.net/qq_39516859/article/details/79794549
版权声明：本文为博主原创文章，转载请附上博文链接！