(中等) HDU 1828 Picture，扫描线。

　　Problem Description

　　A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

　　Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

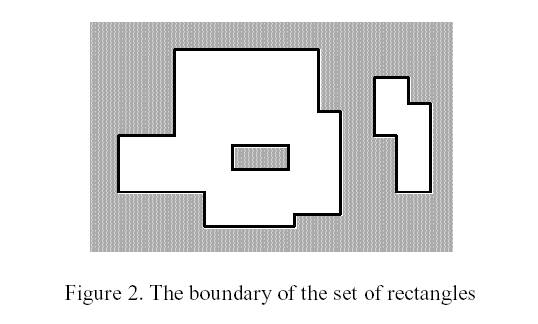
　　The vertices of all rectangles have integer coordinates.

 

　　题目就是求矩形并的周长和。

　　这个题其实和求矩形的面积和没有什么区别，线段树维护的是覆盖区间的总长度，然后扫描线是从左到右扫描，每次计算一个竖边的时候，这一次区间覆盖长度减去上一次区间覆盖长度的绝对值就是变化量，要加到ans上。

　　然后就是计算横边的时候有点麻烦，可以再从下到上扫描一遍，从新弄一个线段树。

　　不过根据那个杭电大神的做法，是同时再维护三个线段树，分别表示区间内线段端点的个数，区间内左边界是否被覆盖，右边界是否被覆盖，后两个线段树是用来辅助计算前面那个的。然后x的差值乘上线段的个数就是横边的了。

　　不过这里要注意先计算还是先更新的问题，横边要先计算，然后更新，然后竖边计算。

 

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>

#define lc po*2
#define rc po*2+1
#define lson L,M,lc
#define rson M+1,R,rc

using namespace std;

const int maxn=;

struct BIAN
{
    int x,y1,y2;
    short state;
};

BIAN bian[];
bool vis[maxn];
int BIT[maxn*];
int COL[maxn*];

bool lBIT[maxn*],rBIT[maxn*];
int coubian[maxn*];

void pushUP(int L,int R,int po)
{
    if(COL[po])
    {
        BIT[po]=R-L+;
        lBIT[po]=rBIT[po]=;
        coubian[po]=;
    }
    else if(L==R)
    {
        BIT[po]=;
        lBIT[po]=rBIT[po]=;
        coubian[po]=;
    }
    else
    {
        BIT[po]=BIT[lc]+BIT[rc];
        lBIT[po]=lBIT[lc];
        rBIT[po]=rBIT[rc];
        coubian[po]=coubian[lc]+coubian[rc];

        if(lBIT[rc]&&rBIT[lc])
            coubian[po]-=;
    }
}

void update(int ul,int ur,int ut,int L,int R,int po)
{
    if(ul<=L&&ur>=R)
    {
        COL[po]+=ut;
        pushUP(L,R,po);

        return;
    }

    int M=(L+R)/;

    if(ul<=M)
        update(ul,ur,ut,lson);
    if(ur>M)
        update(ul,ur,ut,rson);

    pushUP(L,R,po);
}

bool cmp(BIAN a,BIAN b)
{
    return a.x<b.x;
}

int main()
{
    int N;
    int x1,x2,y1,y2;
    int ans,last;

    while(~scanf("%d",&N))
    {
        ans=;
        last=;
        memset(COL,,sizeof(COL));
        memset(BIT,,sizeof(BIT));
        memset(vis,,sizeof(vis));
        memset(lBIT,,sizeof(lBIT));
        memset(rBIT,,sizeof(rBIT));
        memset(coubian,,sizeof(coubian));

        for(int i=;i<=N;++i)
        {
            scanf("%d %d %d %d",&x1,&y1,&x2,&y2);

            bian[i*-].x=x1;
            bian[i*-].y1=y1+;
            bian[i*-].y2=y2+;
            bian[i*-].state=;

            bian[i*].x=x2;
            bian[i*].y1=y1+;
            bian[i*].y2=y2+;
            bian[i*].state=-;
        }

        sort(bian+,bian+*N+,cmp);

        for(int i=;i<=*N;++i)
        {
            ans+=coubian[]*(bian[i].x-bian[i-].x);

            update(bian[i].y1,bian[i].y2-,bian[i].state,,,);

            ans+=abs(BIT[]-last);
            last=BIT[];
        }

        printf("%d\n",ans);
    }

    return ;
}