网格最短路径算法（Dijkstra & Fast Marching）(转)

　　Dijkstra算法是计算图中节点之间最短路径的经典算法，网上关于Dijkstra算法原理介绍比较多，这里不再多讲。值得一提的是，当图中节点之间的权重都为1时，Dijkstra算法就变化为一般意义上的广度优先搜索算法（Breadth-first search algorithm）。

　　Dijkstra算法流程如下：

Dijkstra算法流程

 

　　在介绍Fast marching算法之前先提下Eikonal方程，Eikonal方程属于非线性偏微分方程，可以认为是一种近似波动方程，它的形式如下：

　　Eikonal方程解u(x)的物理含义是从源点x₀以速度f(x)到达计算域Ω内x点所需要消耗的最短时间。当f(x) = 1的特殊情况下，方程解就代表计算域Ω内的距离场。

　　[Sethian et al. 1999]提出的Fast marching算法是一种求解Eikonal方程的数值方法。下面首先以二维正交栅格（栅格间距为h）为例，将方程左边的梯度项用一阶近似代替后可以得到：

max(U – U_A, U – U_B, 0)² + max(U – U_C, U – U_D, 0)² = h²/f(x)²

　　假设U_A = min(U_A, U_B)，U_C = min(U_C, U_D)，那么：

(U – U_A)² + (U – U_C)² = h²/f(x)²

　　当||U_A – U_C || ≤ h/f(x)时，。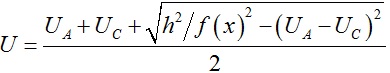

　　当||U_A – U_C || > h/f(x)时，U = min(U_A, U_C) + h/f(x)。

Fast marching算法也可以用于计算三角网格上的测地距离。对于三角面片x₁x₂x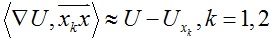，，因此，Eikonal方程可以近似变为如下二次方程：

(a^TQa)U(x)² + (2a^TQb)U(x) + b^TQb = 1/f(x)²，

其中：a = [1;1]，b = –[Ux₁；Ux₂]，M = [x – x₁; x – x₂]，Q = (MM^T) ^–1。通过求解上式方程可以得到x点的测地距离。

　　Fast marching算法流程如下：

Fast marching算法流程

 

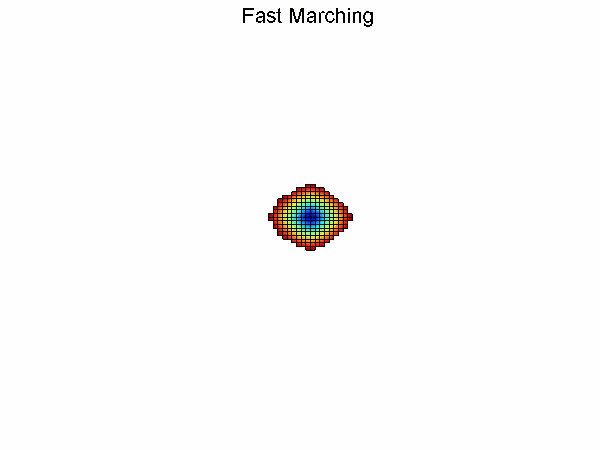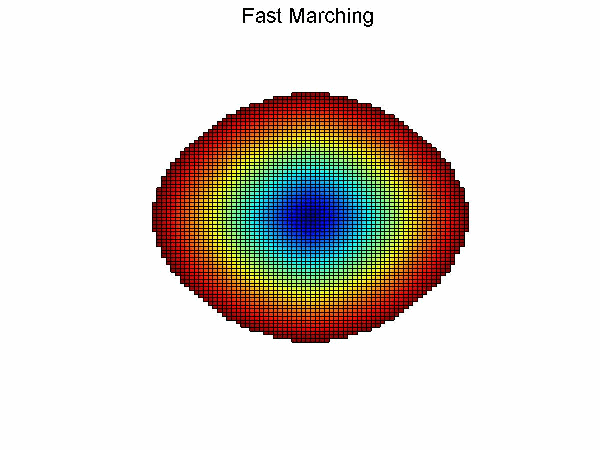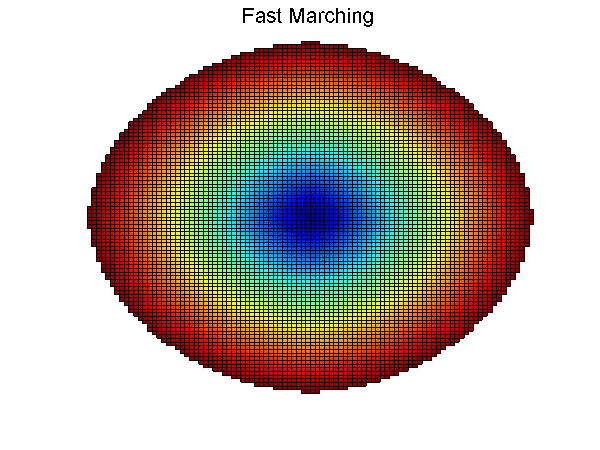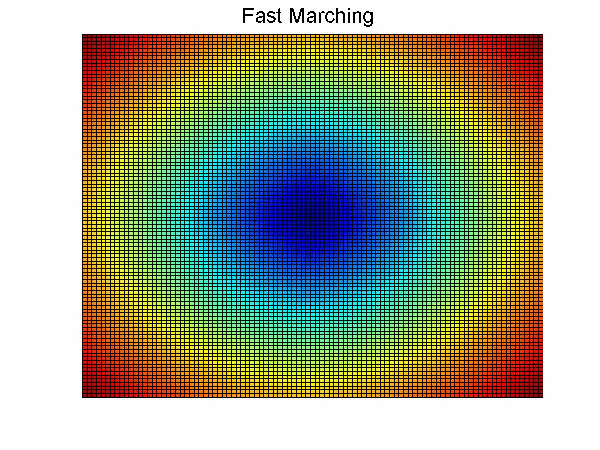
　　Dijkstra算法和Fast marching算法思想相似，不同之处在于Dijkstra算法利用节点之间的欧式距离进行更新，而Fast marching算法利用由Eikonal方程化简得到的近似偏微分方程进行更新。

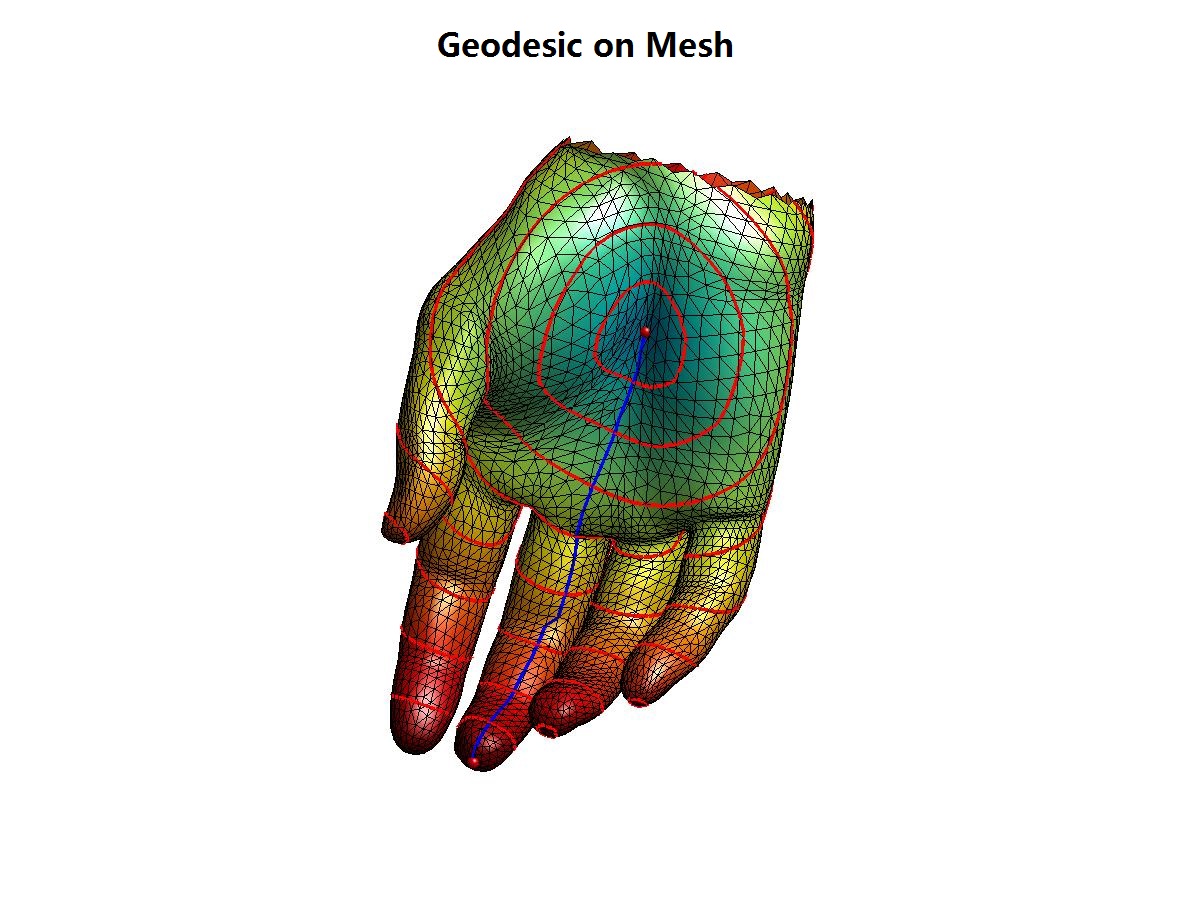
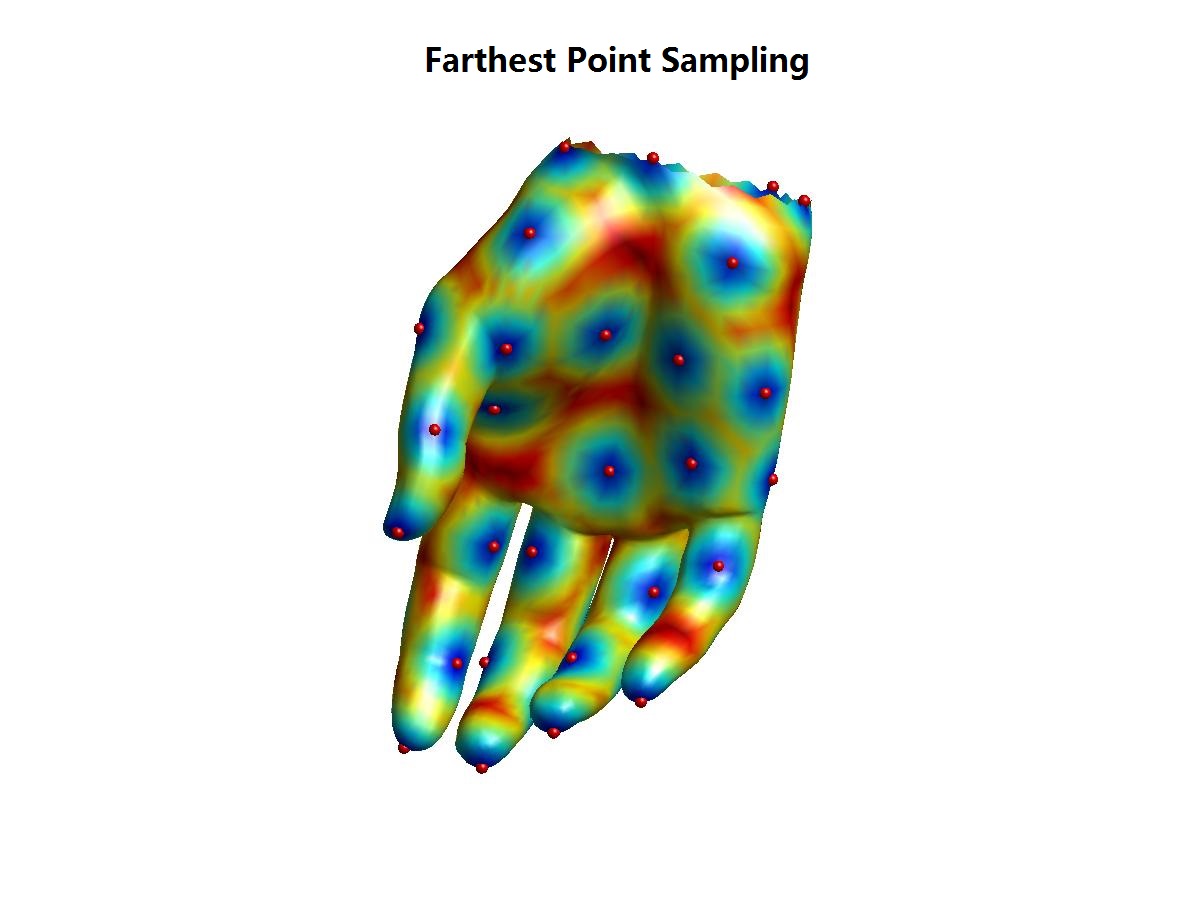
参考文献：

[1] J. A. Sethian, A. Vladimirsky. Fast methods for the eikonal and related Hamilton-Jacobi equations on unstructured meshes. (1999). Proceedings of the National Academy of Sciences, 97(11), 5699-5703.

http://www.cnblogs.com/shushen/p/5381753.html