EM算法 大白话讲解

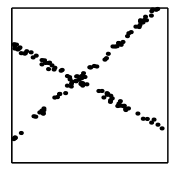
假设有一堆数据点,它是由两个线性模型产生的。公式如下：

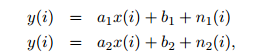
模型参数为a,b,n：a为线性权值或斜率，b为常数偏置量，n为误差或者噪声。

一方面，假如我们被告知这两个模型的参数，则我们可以计算出损失。

对于第i个数据点，第k个模型会预测它的结果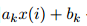

则，与真实结果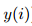的差或者损失记为：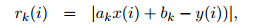

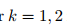
目标是最小化这个误差。

但是仍然不知道具体哪些数据由对应的哪个模型产生的。

另一方面，假设我们被告知这些数据对应具体哪个模型，则问题简化为求解约束条件下的线性方程解

(实际上可以计算出最小均分误差下的解，^-^)。

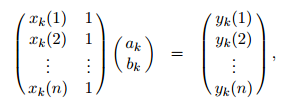
这两个假设，都只知道其中的一部分信息，所以求解困难。

EM算法就是重复迭代上述两步，固定因素A，放开因素B，然后固定因素B，再放开因素A，直到模型收敛，

如此迭代更新估计出模型的输出值以及参数值。

具体如下：

--------------------------------------------------------------------------------------------------------

在E步时，模型参数假定已知(随机初始化或者聚类初始化，后续不断迭代更新参数)，
 计算出每个点属于模型的似然度或者概率(软判决，更加合理，后续可以不断迭代优化，而硬判决不合理是因为之前的假定参数本身不可靠，判决准则也不可靠)。

根据模型参数，如何计算出似然度？

计算出模型输出值与真实值的残差：

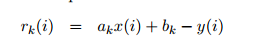
已知残差，计算出i点属于k模型的似然度(残差与似然度建立关系)：

贝叶斯展开

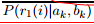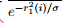 = ，假设残差与概率分布为高斯分布，残差距离度量 转换成  概率度量。

残差越小，则发生概率越大。

根据产生的残差，判断i属于模型k的归属概率

则，

完成点分配到模型的目的

--------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------

进入M步，知道各个点属于对应模型的概率，利用最小均分误差，估计出模型参数

绝对值差*概率，误差期望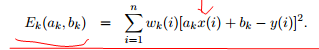最小化

最小化

求偏导：

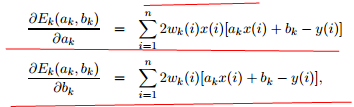
置0，则上述两公式展开为

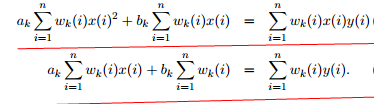
改写成 矩阵式：

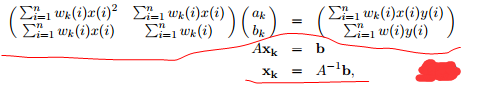
完成计算出ak和bk参数

如此，反复迭代，收敛

EM算法对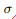敏感，每轮迭代它的更新推荐公式：

--------------------------------------------------------------------------------

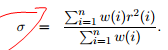
同样地，在 GMM 中，我们就需要确定 影响因子pi(k)、各类均值pMiu(k) 和 各类协方差pSigma(k) 这些参数。 我们的想法是，找到这样一组参数，它所确定的概率分布生成这些给定的数据点的概率最大，而这个概率实际上就等于  ，我们把这个乘积称作似然函数 (Likelihood Function)

没法直接用求导解方程的办法直接求得最大值。

不清楚这类数据是具体哪个高斯生成的，或者说生成的概率。

E步中，确定出数据xi属于第i个高斯的概率：通过计算各个高斯分量的后验概率，占比求得。

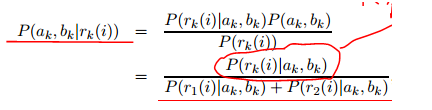
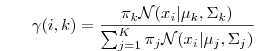
解决了点的归属。

M步中，重新计算出各个参数。

知道了各个点属于各个高斯的概率，可以重新计算求出 均值、方差、权重

如此EM重复。

参考：http://blog.csdn.net/abcjennifer/article/details/8198352

--------------------------------------------------------------------------------------------------------