Java Heap

堆

堆是一种基于树的数据结构，是一种完全二叉树，堆中的所有的节点都按照特定的顺序排列。

在堆数据结构中，如果任意父节点的值都大于其子节点，则会产生一个大顶堆；反之，如果任意父节点的值都小于其子节点，则会产生一个小顶堆 。

上述这种父节点与子节点之间的关系被称为堆属性 。

二叉堆

由于二叉堆是一棵完全二叉树，它可以很容易的被表示为一个数组。在数组中，array[0] 代表根节点，且父节点与子节点的索引关系为：Left Child = 2 * Parent + 1 , Right Child = 2 * Parent + 2。

下图是一个大顶堆的树形结构表示：

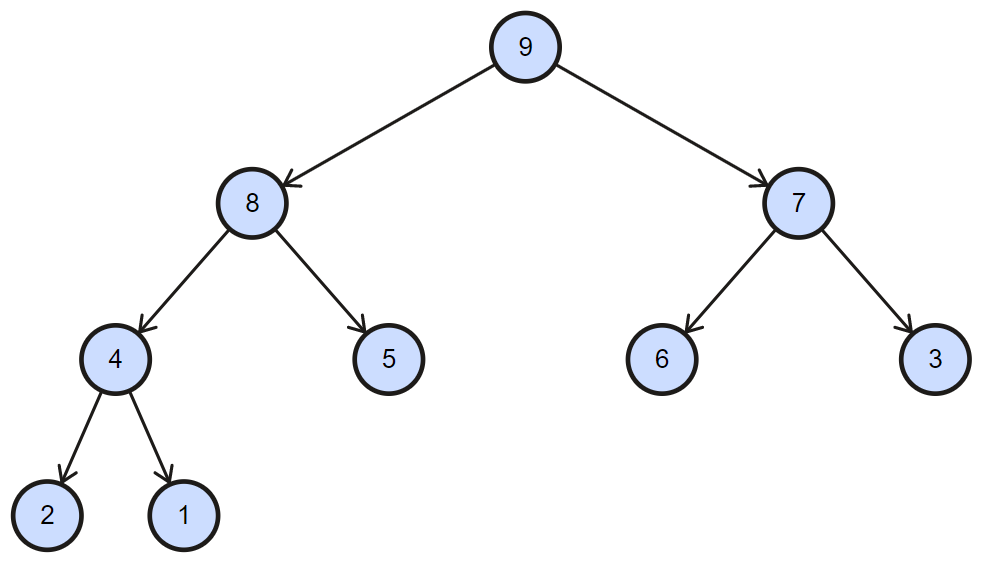
其数组表示如下：

[9, 8, 7, 4, 5, 6, 3, 2, 1]

小顶堆

插入元素

该过程包括两个步骤：

• 将元素插入到堆尾
• 执行 上浮 操作使其满足堆属性，该过程时间复杂度为 \(O(log N)\)

siftup操作逻辑： 对于小顶堆，若当前节点的元素小于其父节点，则交换这俩个节点的值，然后递归父节点，保证满足堆属性。

@SuppressWarnings("unchecked")
private void siftUp(int k, E x) {
  Comparable<? super E> key = (Comparable<? super E>) x;
  while (k > 0) {
    int parent = (k - 1) >>> 1;
    Object e = minHeap[parent];

    if (key.compareTo((E) e) >= 0) {
      break;
    }

    minHeap[k] = e;
    k = parent;
  }

  minHeap[k] = key;
}

删除元素

该过程包括3个步骤：

• 找到待删除元素的索引位置
• 将堆中最后一个元素移动到待删除元素的索引位置
• 对该索引位置元素执行 上浮 或 下沉 操作，该过程时间复杂度为 \(O(log N)\)

siftDown操作逻辑： 对于小顶堆，如果当前节点的值大于其左子节点或右子节点的值，则交换当前节点与子节点中的较小值，然后递归子树保证满足堆属性。

// 将最后一个元素移动到被删除位置
E moved = (E) minHeap[s];
minHeap[s] = null;

// 下沉
siftDown(i, moved);
if (minHeap[i] == moved) {
  /**
   * minHeap[i] == moved
   * 表示没有下沉, 说明当前节点与子节点满足堆属性
   * 执行上浮, 使得当前节点与父节点满足堆属性
   */
  siftUp(i, moved);
  if (minHeap[i] != moved) {
    return moved;
  }
}

private void siftDown(int k, E x) {
  Comparable<? super E> key = (Comparable<? super E>) x;
  int half = heapSize >>> 1;   // 非叶子节点
  while (k < half) {
    int child = (k << 1) + 1;
    int right = (k << 1) + 2;
    Object c = minHeap[child];

    if (right < heapSize && ((Comparable<? super E>) c).compareTo((E) minHeap[right]) > 0) {
      c = minHeap[child = right];
    }

    if (key.compareTo((E) c) <= 0) {
      break;
    }

    minHeap[k] = c;
    k = child;
  }
  minHeap[k] = key;
}

Java 实现

下述代码为小顶堆的实现，大顶堆的实现也是一样的，区别就是上浮 和 下沉 操作的交换逻辑与小顶堆相反。

package DataStructure;

import java.io.Serializable;
import java.util.NoSuchElementException;

public class MinHeap<E> implements Serializable{
  private static final int DEFAULT_INITIAL_CAPACITY = 11;
  transient Object[] minHeap;
  private int heapSize = 0;   // 当前堆中的元素个数
  private int maxSize;    // 堆中最大元素个数

  public MinHeap() {
    this(DEFAULT_INITIAL_CAPACITY);
  }

  public MinHeap(int initialCapacity) {
    if (initialCapacity < 1) {
      throw new IllegalArgumentException();
    }

    this.maxSize = initialCapacity;
    this.minHeap = new Object[initialCapacity];
  }

  public MinHeap(Collection<? extends E> c) {
    initElementsFromCollection(c);
    heapify();
  }

  public int size() {
    return heapSize;
  }

  public void clear() {
    for (int i = 0; i < heapSize; i++) {
      minHeap[i] = null;
    }

    heapSize = 0;
  }

  @SuppressWarnings("unchecked")
  public E peek() {
    return (heapSize == 0) ? null : (E) minHeap[0];
  }

  /**
   * 插入元素到堆尾
   * @param e
   */
  public boolean add(E e) {
    if (e == null) {
      throw new NullPointerException();
    }

    int i = heapSize;
    if (i >= maxSize) {
      throw new NoSuchElementException("Heap is full!");
    }

    if (i == 0) {
      minHeap[0] = e;
    }
    else {
      siftUp(i, e);
    }

    return true;
  }

  /**
   * 删除指定元素
   * @param o
   * @return
   */
  public boolean remove(Object o) {
    int i = indexOf(o);
    if (i == - 1) {
      return false;
    }
    else {
      removeAt(i);
      return true;
    }
  }

  /**
   * 弹出堆顶元素
   * @return
   */
  @SuppressWarnings("unchecked")
  public E poll() {
    if (heapSize == 0) {
      return null;
    }

    int s = --heapSize;
    E result = (E) minHeap[0];
    E x = (E) minHeap[s];
    minHeap[s] = null;
    if (s != 0) {
      siftDown(0, x);
    }

    return result;
  }

  private int indexOf(Object o) {
    if (o != null) {
      for (int i = 0; i < heapSize; i++) {
        if (o.equals(minHeap[i])) {
          return i;
        }
      }
    }

    return -1;
  }

  @SuppressWarnings("unchecked")
  private E removeAt(int i) {
    int s = --heapSize;
    if (s == i) {
      minHeap[i] = null;   // 移除最后一个元素
    }
    else {
      // 将最后一个元素移动到被删除位置
      E moved = (E) minHeap[s];
      minHeap[s] = null;

      // 下沉
      siftDown(i, moved);
      if (minHeap[i] == moved) {
        // 没有下沉, 说明当前节点与子节点满足堆属性
        // 执行上浮, 使得当前节点与父节点满足堆属性
        siftUp(i, moved);
        if (minHeap[i] != moved) {
          return moved;
        }
      }
    }

    return null;
  }

  @SuppressWarnings("unchecked")
  private void siftUp(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
      int parent = (k - 1) >>> 1;
      Object e = minHeap[parent];

      if (key.compareTo((E) e) >= 0) {
        break;
      }

      minHeap[k] = e;
      k = parent;
    }

    minHeap[k] = key;
  }

  @SuppressWarnings("unchecked")
  private void siftDown(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    int half = heapSize >>> 1;   // 非叶子节点
    while (k < half) {
      int child = (k << 1) + 1;
      int right = (k << 1) + 2;
      Object c = minHeap[child];

      if (right < heapSize && ((Comparable<? super E>) c).compareTo((E) minHeap[right]) > 0) {
        c = minHeap[child = right];
      }

      if (key.compareTo((E) c) <= 0) {
        break;
      }

      minHeap[k] = c;
      k = child;
    }
    minHeap[k] = key;
  }

  private void initElementsFromCollection(Collection<? extends E> c) {
    Object[] a = c.toArray();
    if (a.getClass() != Object[].class) {
      a = Arrays.copyOf(a, a.length, Object[].class);
    }

    int len = a.length;
    for (int i = 0; i < len; i++) {
      if (a[i] == null) {
        throw new NullPointerException();
      }
    }

    this.minHeap = a;
    this.heapSize = a.length;
  }

  /**
   * 根据 minHeap 数组建立小顶堆
   */
  @SuppressWarnings("unchecked")
  private void heapify() {
    // 对所有非叶子节点执行下沉操作
    for (int i = (heapSize >>> 1) - 1; i >= 0; i--) {
      siftDown(i, (E) minHeap[i]);
    }
  }
}

优先级队列

PriorityQueue 是堆的一个实现，其默认为小顶堆，可以传入一个比较器使其实现为大顶堆。

public static void main(String[] args) {
  // 默认创建小顶堆
  PriorityQueue<Integer> minQueue = new PriorityQueue<>();

  // 传入比较器, 创建大顶堆
  PriorityQueue<Integer> maxQueue = new PriorityQueue<>((o1, o2) -> {return o2 - o1;});

  for (int i = 0; i < 10; i++) {
    minQueue.add(i);
    maxQueue.add(i);
  }

  Iterator<Integer> it1 = minQueue.iterator();
  Iterator<Integer> it2 = maxQueue.iterator();
  while (it1.hasNext()) {
    System.out.print(it1.next() + " ");
  }
  System.out.println();

  while (it2.hasNext()) {
    System.out.print(it2.next() + " ");
  }
  System.out.println();
}

输出结果为：

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

[9, 8, 5, 6, 7, 1, 4, 0, 3, 2]

堆排序

堆排序算法步骤如下 (升序排列)：

• 对待排序数组建立小顶堆
• 依次弹出堆顶元素即堆中最小值

该算法时间复杂度为：\(O(NlogN)\)

public static void main(String[] args) {
  int[] nums = {2, 3, 1, 6, 4, 7, 5, 8, 9};
  List<Integer> list = Arrays.stream(nums).boxed().collect(Collectors.toList());
  MinHeap<Integer> minHeap = new MinHeap<>(list);

  int[] res = new int[nums.length];
  int index = 0;
  while(minHeap.size() != 0) {
    res[index++] = minHeap.poll();
  }

  for (int i = 0; i < res.length; i++) {
    System.out.print(res[i] + " ");
  }
  System.out.println();
}

输出结果为：[1, 2, 3, 4, 5, 6, 7, 8, 9]