【python_PAT_乙类】1007_素数对猜想 ，Python运行超时解决方案

题目：

让我们定义d​n​​为：d​n​​=p​n+1​​−p​n​​，其中p​i​​是第i个素数。显然有d​1​​=1，且对于n>1有d​n​​是偶数。“素数对猜想”认为“存在无穷多对相邻且差为2的素数”。
现给定任意正整数N(<)，请计算不超过N的满足猜想的素数对的个数。
输入格式:
输入在一行给出正整数N。
输出格式:
在一行中输出不超过N的满足猜想的素数对的个数。

输入样例:
20
输出样例:
4

　思路：

1、常规判断素数，i+2 的值与 i进行比较（以3开始，且偶数排除），超时

2、开根号判断素数，以素数生成一个列表（以3开始，且偶数排除），列表里进行比较，超时

3、开根号判断素数，根据特性，判断当前是不是素数，不是素数，判断列表的最后一位与当前是不是差2，如果差2则移除列表最后一项值，保证列表中的值是既是素数且有素数对，在最终生成的列表项的最后一项需要做额外处理，需要判断最后1项是否有素数对。

代码如下：

 1 # 素数对猜想
 2 import math
 3
 4
 5 def is_prime_num(test_num):
 6     for i in range(3, int(math.sqrt(test_num)+1), 2):
 7         if test_num % i == 0:
 8             return False
 9     return True
10
11
12 num = int(input())
13 count_num = 0
14 i = 3
15 list_num = []
16 while 2 < i <= num-2:
17     if is_prime_num(i):
18         list_num.append(i)
19     elif i - list_num[-1] == 2:
20         del list_num[-1]
21     i = i + 2
22 if (not is_prime_num(num)) and num - list_num[-1] == 2:
23     del list_num[-1]
24 print(len(list_num))

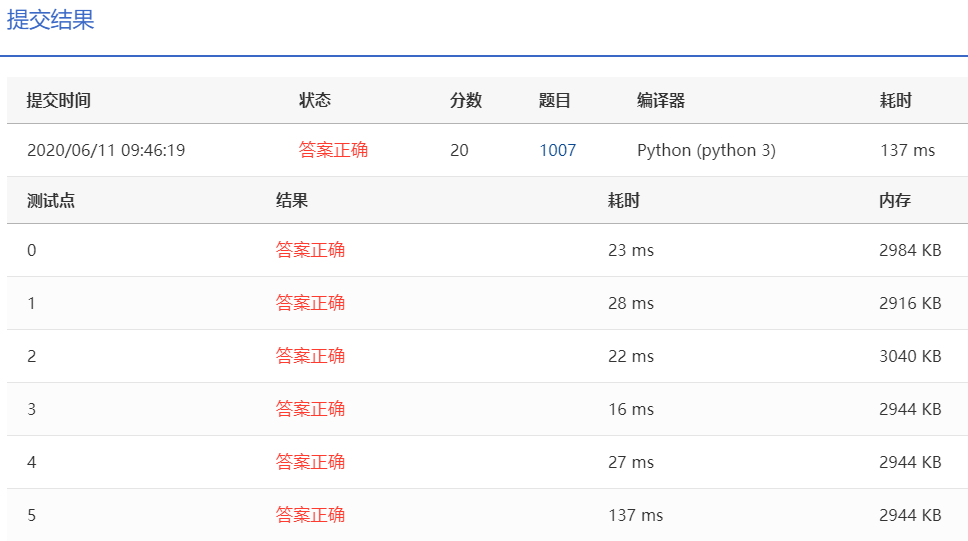
运行结果：