题目分享V

题意：现在两个人做游戏，每个人刚开始都是数字1，谁赢了就能乘以k^2，输的乘以k（k可以是任意整数，每次不一定相同）现在给你最终这两个人的得分，让你判断是否有这个可能，有可能的话Yes，否则No。

分析：这题其实想起来也很好想，写起来也很好写，主要还是分享一下处理类似细节的方法

　　首先还是先回归到这个题，显然如果满足条件，首先a*b=x³，a，b分别为这两人的最终得分，然后考虑一下还需满足什么性质

　　我们还是从只有一轮开始考虑，a=k²，b=k，a*b=k³，这里就很容易想到几种判断方法，比如a=b²，或者a/b=k=³√a*b，等等，只要这个判断方法只与a与b有关就行（废话）

　　再考虑两轮的情况，a=k1²*k2²，b=k1*k2，这看上去上面两种方法都会判断为yes，答案也真就是yes

　　但如果a=k1²*k2，b=k1*k2²，这样看上去好像两种方法都会判断为no，而正确结果应该是yes，

　　那么到底应该怎么做呢？

　　不难发现的是，无论这两个数怎么变换，a=k1^c1*k2^c2*k3^c3……*kn^cn，b=a=k1^d1*k2^d2*k3^d3……*kn^dn，其中ci+di=3

　　a和b都是在k1*k2*k3*……*kn到k1²*k2²*k3²*……*kn²之间浮动，而且他们显然都满足一个性质即能整除k1*k2*……*kn=³√a*b、*

　　那么我们大胆假设，满足a*b=x³且a，b能整除³√a*b的数一定满足条件吗

/*　　这对于k1，k2，……，kn互质来说一定是显然成立的，但如果不一定互质，那可能很多人就有些犹豫或者迷糊

　　既然这样，那么我们就把不互质的转化成互质的

　　很容易想到，每一个ki^ci或di都会变成p1^e1^ci*p2^e2^ci*……*pn^en^ci，当然这里的pi是质数，而ei则是非负整数，当然上面的结论也要搬过来，e1*ci+e1*di=3（这里前面一个e1是指a中ki的系数，后一个是b中的）

　　a=p1^f1*p2^f2*p3^f3……*pn^fn，b=p1^g1*p2^g2*p3^g3……*pn^gn，这里的fi=每个ki的ei与ci的乘积，（写起来变量名太容易冲突了，理解就行）

　　当然，联系上面的结论，很容易得到fi+gi=3h，

　　说了这么多，可能很多人都忘了我们要干啥了，现在我们把不互质的转化成了互质的，显然这里面fi的最小值还是h，所以也就得证了

*/　　当然，我这上面证明的有点乱，但其实真的很好证，当然如果不会证也没关系，而且今天我主要分享的也不是这个，这个/*   */的大可以不看

　　先再梳理一下，我们只需要保证a*b=x³且a%x==0&&b%x==0即可　

　　那么如何判断a*b是不是立方数呢？

　　当然我们可以二分，不过cmath里面pow这个函数给了我们方便

　　有些人可能只知道p=pow（q，2），不知道p=pow（q，1/2）

　　对，这其实就与sqrt等价了

　　那么这个题我求出了pow(a*b,1/3)然后呢？

　　只需要判断这个数是不是整数即可，那这又咋判断呢？

　　首先我们要知道的是double是有精度的，一般为6-7位，具体是什么意思呢？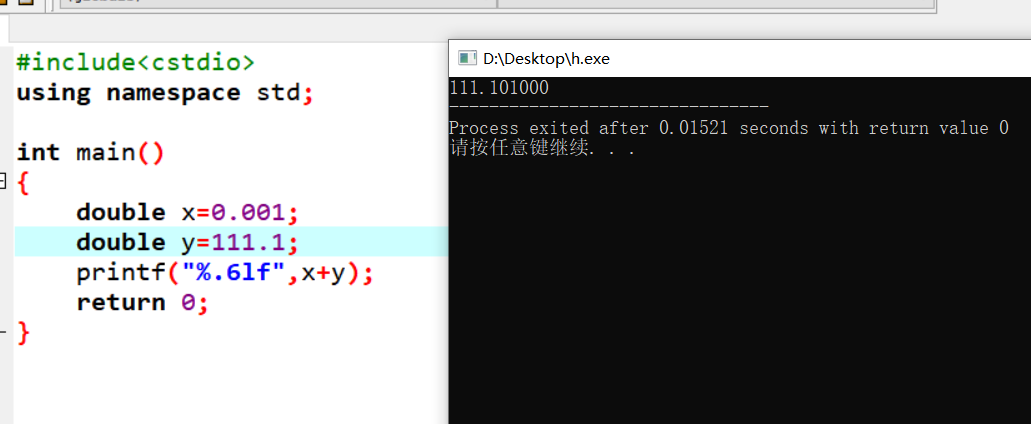

这显然没啥问题

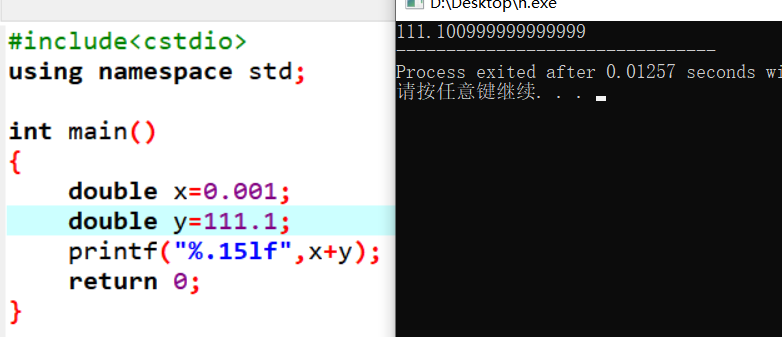
这问题就出来了，而且这不光是在小数的时候，整数运算虽然问题不是很大，但也要小心

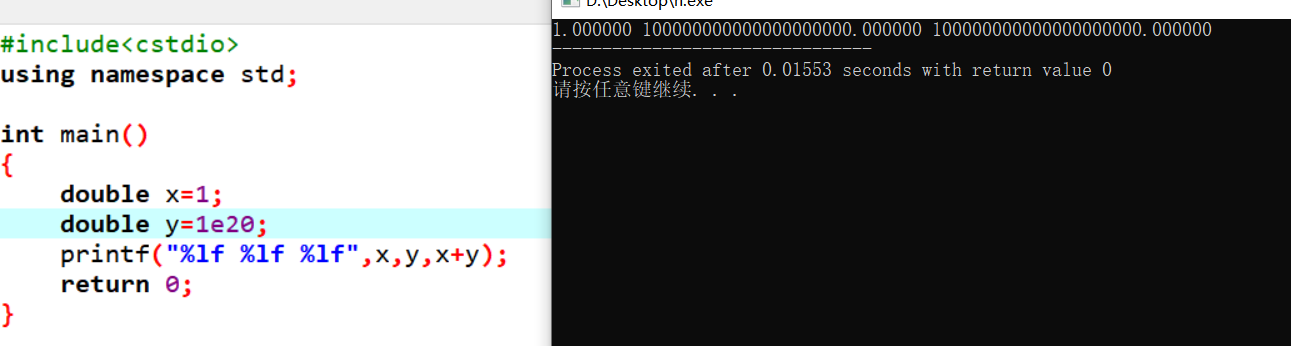
当然，不需要太过紧张，首先我这里y是1e20，都超过longlong的范围了，而上面的999999在你保留6，7位的时候也是完全没有影响的，但却有可能产生0.000001的误差

这在平日的输出结果中没有任何影响，但在判断是否相等或者将其赋值给int以求取整时便会有着灾难性的问题出现，比如

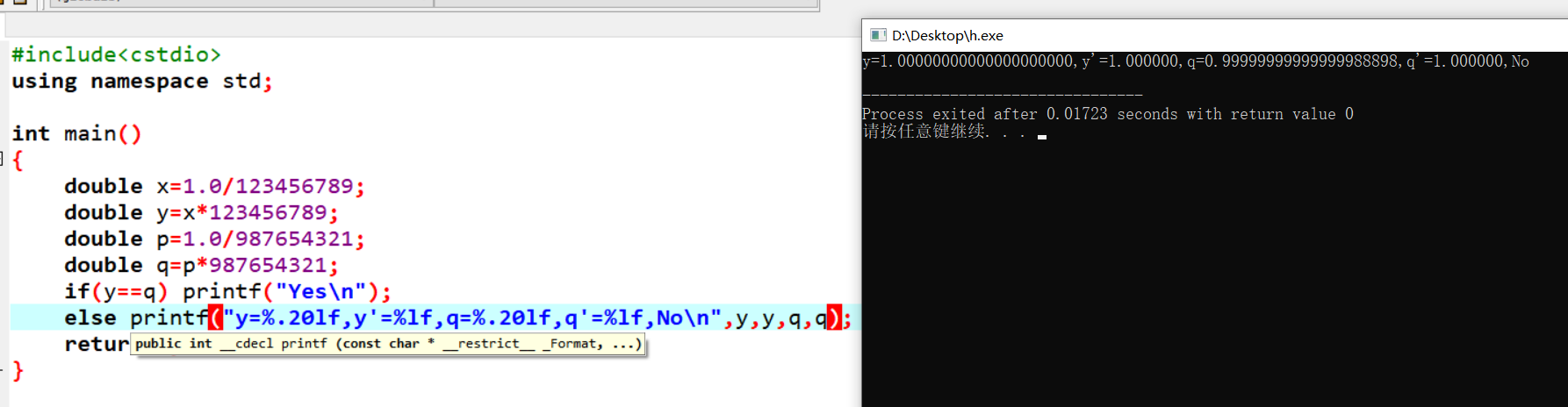
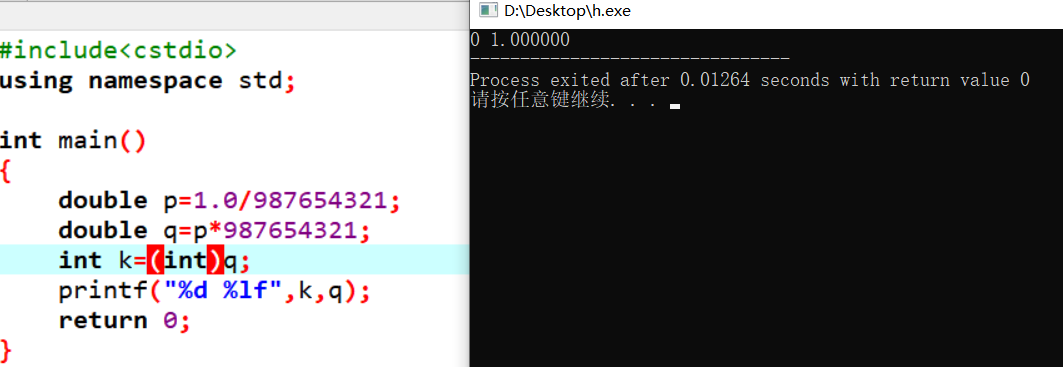
这里就需要利用我们的精度了

如果我们要表达y==q要改成abs(y-q)<=0.000001

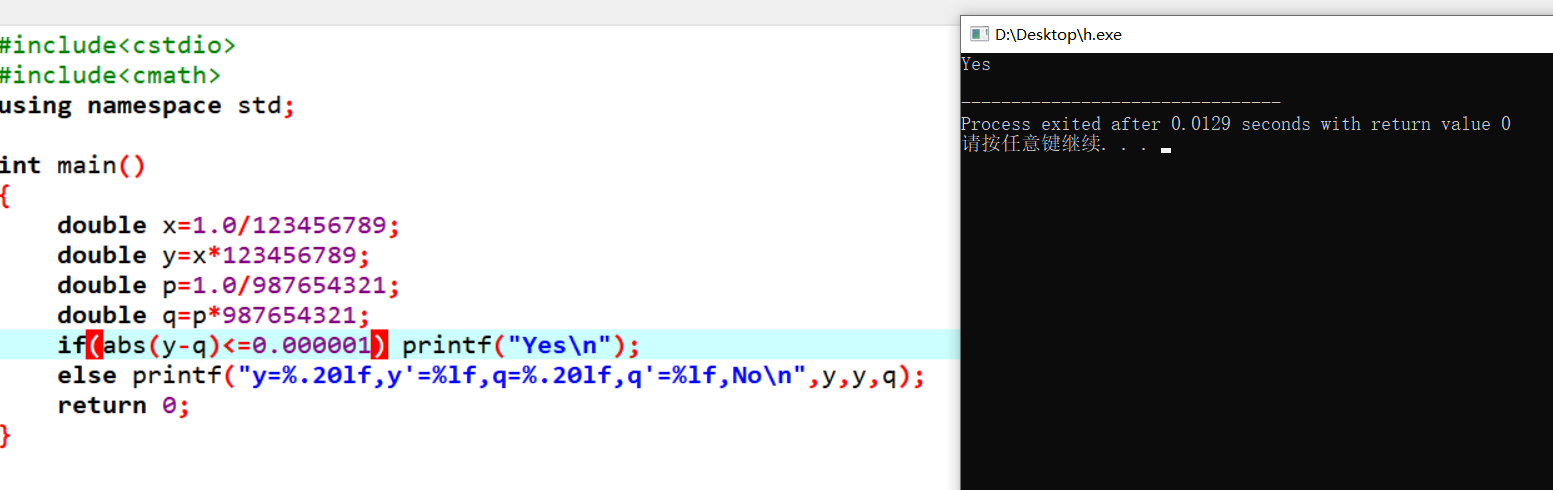
而如果我们要表达k=(int)q要改成k=(int)(q+0.000001)

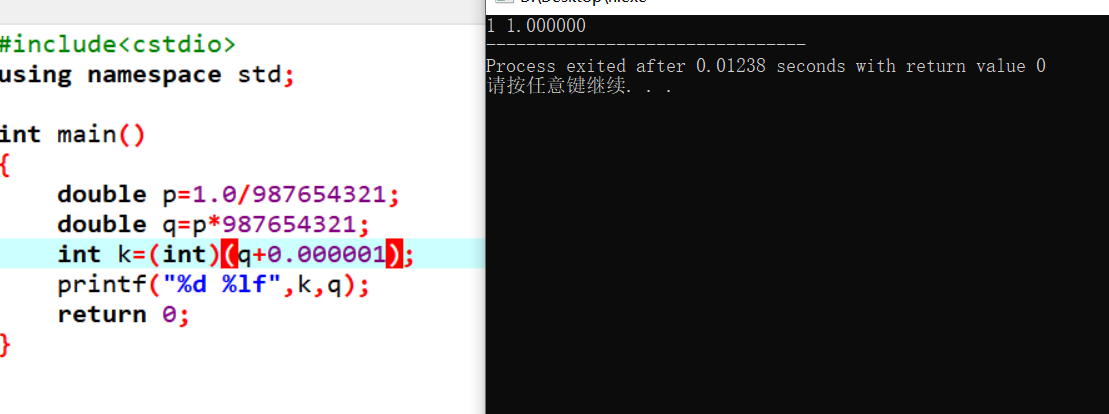
所以又说了这么多，再回到开始的问题，我们需要判断这个数是否是整数，那么就可以用abs(x-(int)(x+0.000001))<=0.000001来判断

还有几点要注意的，

1. a*b可能爆int

2. pow里面后面那个要写1.0/3,如果写1/3的话就成0了（1/3是int类型的）

3. Yes还是YES还是yes，No还是NO还是no看清楚

代码：

#include<cstdio>
#include<cmath>
using namespace std;

#define ll long long

const double minlf=0.000001;

int pd(ll x)
{
    double sq=pow(x,1.0/);
    int sqr=(int)(sq+minlf);
    if(abs((double)sqr-sq)<=minlf) return sqr;
    else return ;
}

int main()
{
    int n,x,y;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d%d",&x,&y);
        int now=pd((ll)x*y);
        if(now&&x%now==&&y%now==) printf("Yes\n");
        else printf("No\n");
    }
    return ;
}