POJ 2142：The Balance

The Balance

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 4781		Accepted: 2092

Description

Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of aspirin using 300mg weights and 700mg weights, she can put one 700mg weight on the side of the medicine and three 300mg weights
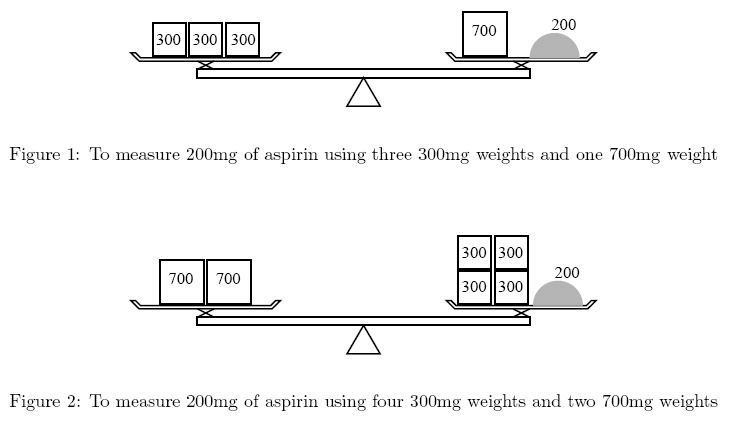
on the opposite side (Figure 1). Although she could put four 300mg weights on the medicine side and two 700mg weights on the other (Figure 2), she would not choose this solution because it is less convenient to use more weights. 

You are asked to help her by calculating how many weights are required. 

Input

The input is a sequence of datasets. A dataset is a line containing three positive integers a, b, and d separated by a space. The following relations hold: a != b, a <= 10000, b <= 10000, and d <= 50000. You may assume that it is possible to measure d mg using
a combination of a mg and b mg weights. In other words, you need not consider "no solution" cases. 

The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.

Output

The output should be composed of lines, each corresponding to an input dataset (a, b, d). An output line should contain two nonnegative integers x and y separated by a space. They should satisfy the following three conditions.

• You can measure dmg using x many amg weights and y many bmg weights.
• The total number of weights (x + y) is the smallest among those pairs of nonnegative integers satisfying the previous condition.
• The total mass of weights (ax + by) is the smallest among those pairs of nonnegative integers satisfying the previous two conditions.

No extra characters (e.g. extra spaces) should appear in the output.

Sample Input

700 300 200
500 200 300
500 200 500
275 110 330
275 110 385
648 375 4002
3 1 10000
0 0 0

Sample Output

1 3
1 1
1 0
0 3
1 1
49 74
3333 1

题意是给出了a，b，d的重量。问使用a、b怎么测出d的重量，假设是能够测出的前提下。输出|x|+|y|的最小值。

a*x+b*y=d

之后求一下x的最小值时y的值。再求一遍y的最小值时x的值。两两比较即可。

代码：

#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
 
int xx,yy,yue;
int a,b,d;
vector <int> x_value;
vector <int> y_value;
 
void ex_gcd(int a,int b, int &xx,int &yy)
{
	if(b==0)
	{
		xx=1;
		yy=0;
		yue=a;
	}
	else
	{
		ex_gcd(b,a%b,xx,yy);
 
		int t=xx;
		xx=yy;
		yy=t-(a/b)*yy;
 
	}
}
 
void cal()
{
	int i;
	int min=abs(x_value[0])+abs(y_value[0]);
	int min_x=abs(x_value[0]),min_y=abs(y_value[0]);
 
	for(i=1;i<2;i++)
	{
		if(abs(x_value[i])+abs(y_value[i])==min)
		{
			if((abs(x_value[i])*a+abs(y_value[i])*b)<(min_x*a+min_y*b))
			{
				min_x=abs(x_value[i]);
				min_y=abs(y_value[i]);
			}
		}
		if(abs(x_value[i])+abs(y_value[i])<min)
		{
			min=abs(x_value[i])+abs(y_value[i]);
			min_x=abs(x_value[i]);
			min_y=abs(y_value[i]);
		}
	}
	cout<<min_x<<" "<<min_y<<endl;
}
 
int main()
{
	while(cin>>a>>b>>d)
	{
		if(a==0 && b==0 && d==0)
			break;
		ex_gcd(a,b,xx,yy);
 
		x_value.clear();
		y_value.clear();
 
		xx=xx*(d/yue);
		yy=yy*(d/yue);
 
		int r=a/yue;
		yy=(yy%r+r)%r;
		int xx0,yy0=yy;
		xx0=(d-yy*b)/a;
		x_value.push_back(xx0);
		y_value.push_back(yy);
 
		r=b/yue;
		xx=(xx%r+r)%r;
		x_value.push_back(xx);
		yy=(d-xx*a)/b;
		y_value.push_back(yy);
		cal();
	}
	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。