P3376 【模板】网络最大流( Edmonds-krap、Dinic、ISAP 算法)

P3376 【模板】网络最大流( Edmonds-krap、Dinic、ISAP 算法)

题目描述 如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入格式 第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式 一行，包含一个正整数，即为该网络的最大流。

输入输出样例

输入 #1 复制
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40
输出 #1 复制
50

说明/提示

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=25

对于70%的数据：N<=200，M<=1000

对于100%的数据：N<=10000，M<=100000

样例说明：

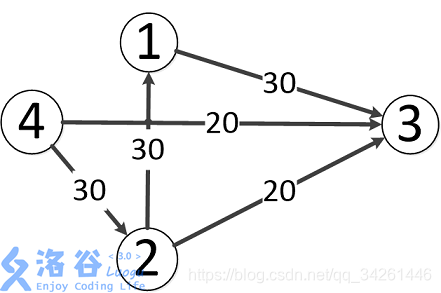
题目中存在3条路径：

4–>2–>3，该路线可通过20的流量

4–>3，可通过20的流量

4–>2–>1–>3，可通过10的流量（边4–>2之前已经耗费了20的流量）

故流量总计20+20+10=50。输出50。

思路

最大流板子。。。。

大佬博客传送门1

传送门2

传送门3

传说门4

题解一（Edmonds-krap）

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;

#define INF 0x3f3f3f3f
const int maxn = 10005;
const int maxm = 300005;
int n,m,s,e;

struct Edge
{
    int u,v,next;
    int cap,flow;
} edge[2*maxm];
int head[2*maxm];

int k = -1;
void Add(int u, int v, int w)
{
    edge[++ k] = (Edge){ u, v, head[u], w, 0};
    head[u] = k;
    edge[++ k] = (Edge){ v, u, head[v], 0, 0};
    head[v] = k;
}
int flag = 0;  //flag == 0 表示还能找到增广路

int bfs(int s, int e)
{
    int min_flow[maxn];     //min_flow[i] 表示到达第 i 号节点时，之前所有的路径中 最小的 边的流量cap - 已经流过的流量flow
    int pre[maxm];          //记录增光路时，当前节点是由那个那条边找到的，这样在找到增光路之后，我们可以根据 pre[] 数组回推其他 组成该增光路的边
    memset(min_flow, 0, sizeof(min_flow));       //min_flow[i] == 0 表示之前没有走过 i 节点
    min_flow[s] = INF;
    pre[s] = -1;
    queue<int> q;
    q.push(s);
    int u,v,flow;
    while(! q.empty())
    {
        u = q.front(); q.pop();

        for(int i = head[u]; i != -1; i = edge[i].next)
        {
            v = edge[i].v;
            flow = edge[i].cap - edge[i].flow;
            if(flow > 0 && ! min_flow[v])   //所走的这条边还有 剩余的空间cap，并且该节点还没有被走过。。
            {
                pre[v] = i;
                min_flow[v] = min(min_flow[u], flow);
                q.push(v);
            }
        }
        if(min_flow[e])
            break;
    }
    if(! min_flow[e])       //一只到更新结束，终点到最小增加值还是等于0，那么说从起点到终点已经没有增广路了
        flag = 1;
    //这一点千万不要忘，，，，把用过的水流在这条增光路上都减去。。。。
    for(int j = e; pre[j] != -1;  j = edge[pre[j]].u)
    {
        edge[pre[j]].flow += min_flow[e];
        edge[pre[e]^1].flow -= min_flow[e];
    }
    return min_flow[e];     //返回最小增加值到 答案中
}

int max_flow()
{
    int mx_flw = 0;
    while(1)
    {
        mx_flw += bfs(s, e);
        if(flag)
            break;
    }
    return mx_flw;
}

void init()
{
    memset(head, -1, sizeof(head));
    k = -1;
}

int main()
{
    ios::sync_with_stdio(false); cin.tie(nullptr);
    //freopen("T.txt","r",stdin);
    cin >> n >> m >> s >> e;
    init();
    int u,v,w;
    for(int i = 1; i <= m; i ++)
    {
        cin >> u >> v >> w;
        Add(u, v, w);
    }
    cout << max_flow() << endl;

    return 0;
}

---

题解二（Dinic）

#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;

#define INF 1e9
#define ll long long
const int maxn = 100005;
const int maxm = 150000;
int n,m;

struct Edge
{
    int v;
    ll w;
    int next;
} edge[maxm];
int head[maxn], cur[maxn];
int deep[maxn];

int k;
void Add(int u, int v, ll w)
{
    edge[++ k] = (Edge){ v, w, head[u]};
    head[u] = k;
    edge[++ k] = (Edge){ u, 0, head[v]};
    head[v] = k;
}
//bfs 为图分层

bool bfs(int s, int e)
{
    memset(deep, 0x7f, sizeof(deep));
    for(int i = 1; i <= n; i ++) cur[i] = head[i];
    deep[s] = 0;
    queue<int> q;
    q.push(s);
    int u,v;
    ll w;
    while(! q.empty())
    {
        u = q.front(); q.pop();

        for(int i = head[u]; i != -1; i = edge[i].next)
        {
            v = edge[i].v;
            w = edge[i].w;
            if(w && deep[v] > INF)
            {
                deep[v] = deep[u] + 1;
                q.push(v);
            }
        }
    }
    if(deep[e] >= INF)
        return false;
    return true;
}

//dfs 一次找多条增光路（相当于找了一个增广网。。）
ll dfs(int now, int e, ll limit)
{
    if(! limit || now == e) return limit;

    ll flow = 0, f;
    for(int i = cur[now]; i != -1; i = edge[i].next)
    {
        cur[now] = i;   //千万注意这一步的意思啊。。这一步是因为 dfs的特性是每次增广一定是增广，那么下一次就不必再检查它了，而直接看第一个未被检查的边
        if(deep[edge[i].v] == deep[now] + 1 && (f = dfs(edge[i].v, e, min(limit, edge[i].w))))
        {
            flow += f;
            limit -= f;
            edge[i].w -= f;
            edge[i^1].w += f;
            if(! limit)
                break;
        }
    }
    return flow;
}

ll Dinic(int s, int e)
{
    ll mx_flw = 0;
    while(bfs(s, e))
        mx_flw += dfs(s, e, INF);
    return mx_flw;
}

void init()
{
    k = -1;
    memset(head, -1, sizeof(head));
}

int main()
{
    ios::sync_with_stdio(false); cin.tie(0);
    //freopen("T.txt","r",stdin);
    int s,e;
    cin >> n >> m >> s >> e;
    init();
    int u,v;
    ll w;
    for(int i = 1; i <= m; i ++)
        cin >> u >> v >> w, Add(u, v, w);
    cout << Dinic(s, e);

    return 0;
}

---

题解三（ISAP）

#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;

#define INF 1e9
const int maxn = 10005;
const int maxm = 200005;
int n, m, s, e;
int k;

struct Edge
{
    int v,w,next;
} edge[2 * maxm];

int head[maxn],cur[maxn],deep[maxn];
int last[maxm];
int num[maxm];      // num 桶，用来统计每个分层的节点的数量

void Add(int u, int v, int w)
{
    edge[++ k] = (Edge){ v, w, head[u]};
    head[u] = k;
    edge[++ k] = (Edge){ u, 0, head[v]};
    head[v] = k;
}

//bfs 用于更新deep层
void bfs(int e)
{
//    for(int i = 0; i <= n; i ++)
//        cur[i] = head[i], deep[i] = n;
    for(int i = 0; i <= m; i ++) cur[i] = head[i];
    for(int i = 1; i <= n; i ++) deep[i] = n;
    deep[e] = 0;
    queue<int> q;
    q.push(e);
    int u, v, w;
    while(! q.empty())
    {
        u = q.front(); q.pop();

        for(int i = head[u]; i != -1; i = edge[i].next)
        {
            v = edge[i].v;
            if(edge[i^1].w && deep[v] == n)      //正图 边存在 且 v这个节点没有被求过
            {
                deep[v] = deep[u] + 1;
                q.push(v);
            }
        }
    }
}

int Add_flow(int s, int e)
{
    int ans = INF;
    int now = e;
    while(now != s)
    {
        ans = min(ans, edge[last[now]].w);
        now = edge[last[now]^1].v;
    }
    now = e;
    while(now != s)
    {
        edge[last[now]].w -= ans;
        edge[last[now]^1].w += ans;
        now = edge[last[now]^1].v;
    }
    return ans;
}

int isap(int s, int e)
{
    int now = s;    //从起点开始进行操作
    bfs(e);         //先找出来一条边 被操作的增光路
    for(int i = 1; i <= n; i ++) num[deep[i]] ++;
    int mx_flw = 0;
    while(deep[s] < n)
    {
        if(now == e)        //如果到达汇点直接增广，重新回到源点进行下一轮增广
        {
            mx_flw += Add_flow(s, e);
            now = s;
        }
        bool has_find = 0;
        for(int i = cur[now]; i != -1; i = edge[i].next)
        {
            if(edge[i].w && deep[now] == deep[edge[i].v] + 1)
            {
                has_find = 1;   //做标记已经找到一种可行路径
                cur[now] = i;     //优化当前弧
                now = edge[i].v;
                last[edge[i].v] = i;
                break;
            }
        }

        if(! has_find)
        {
            int minn = n - 1;
            for(int i = head[now]; i != -1; i = edge[i].next)
                if(edge[i].w)
                    minn = min(minn, deep[edge[i].v]);
            if( (-- num[deep[now]]) == 0) break;   //gap 优化出现了断层
            num[deep[now] = minn + 1] ++;
            cur[now] = head[now];
            if(now != s)
                now = edge[last[now]^1].v;
        }
    }
    return mx_flw;
}

void init()
{
    k = -1;
    memset(head, -1, sizeof(head));
}

int main()
{
    ios::sync_with_stdio(false); cin.tie(0);
    //freopen("T.txt","r",stdin);
    cin >> n >> m >> s >> e;
    init();
    int u,v,w;
    for(int i = 1; i <= m; i ++)
        cin >> u >> v >> w, Add(u, v, w);
    cout << isap(s, e);
    return 0;
}

---