python的列表list和集合set操作

以下是一些python的list和set的基本操作

1.list的一些操作

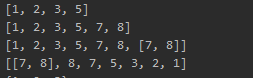
list = [1, 2, 3]
list.append(5)
print(list)

list.extend([7, 8])  # extend是将可迭代对象的元素依次加入列表
print(list)

list.append([7, 8])  # append是把传入的参数当成一个元素加入列表
print(list)

list.reverse()  # 元素翻转，注意不能将这个操作赋给一个变量，此操作是对list本身操作，即list自身发生变化
# l=list.reverse() l为空，没有得到list翻转后的值
print(list)

输出结果：

2.set基本操作：

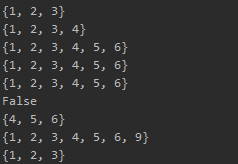
list = [1, 1, 3, 2, 3]
s = set(list)
print(s)

s.add(4)
# s.add([2,3]) 错误，add函数只能增加与原集合相同类型的元素
print(s)

s.update([3, 5, 6])
# s.update(5) 错误，update更新集合时传入的是一个可迭代对象
print(s)

c = s.copy()  # 用于集合复制,创建新集合
cc = s
print(c)
print(cc)
# 类似于list中copy方法
print(cc is c)

ss = {1, 2, 3, 9}
minus = s.difference(ss)  # 求差集
print(minus)

union = s.union(ss)  # 求并集
print(union)

intersection = s.intersection(ss)  # 求交集
print(intersection)

输出结果：