题解 NOIP2018【赛道修建】—— 洛谷

这道题有一点点树上dp的意思（大佬轻喷

我刚拿到这道题的时候毫无头绪，只知道这道题要二分答案

为什么是二分答案？？？

题目:

目前赛道修建的方案尚未确定。你的任务是设计一

种赛道修建的方案，使得修建的 m 条赛道中长度

最小的赛道长度最大（即 m 条赛道中最短赛道的

长度尽可能大）

通常情况下出现 最小的……最大 或者 最大的……最小 时就是二分答案。

如何二分答案？？？

这道题问的是最小的长度最大， 那一定是

二分长度， 即我们可以先设开始时

l = 0， r = 最大值  mid = (l + r) / 2

我们求出的每一条长度大于等于mid的赛道我们称之为合法, 如果合法的赛道数大于m， 那么说明mid <= 真实答案， 所以我们就让 l = mid + 1，继续二分， 否则就让 r = mid。

如何转移？？？

其实刚开始瞎做的时候我并没有发现这是个树上dp（逃

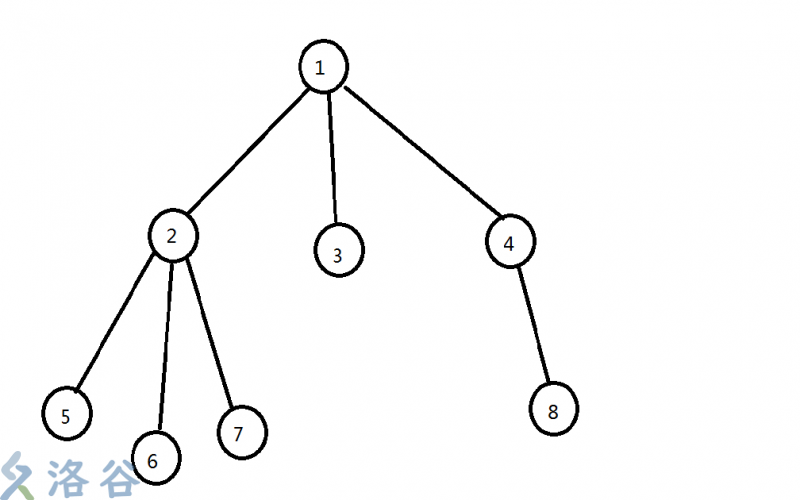
有这么一个图，我们先从每个子树考虑

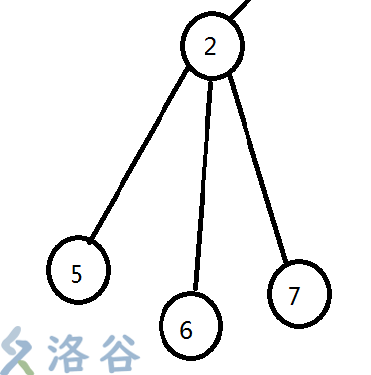
我们假设， 2这个节点为根的子树中，从5到2再到7的这条路径是满足条件的合法赛道，那么我们可以直接答案加1， 然后把这两条边删去。

那么可能会剩下几条边。

我们可以发现， 如果要用2这个节点去构成长度合法的赛道， 要么是2节点开始从0往上走，去凑出合法长度， 要么是挑一个2下面的边（我们先假设为6到2这条边）往上去凑， 最多只能挑一条的边，那么我们一定是要挑一条没用过的最长的边。

n = 50000， 我们可以用multiset的lower_bound来实现每个节点的边的有序和查找某条边是否可以凑成合法的边。

这可以这么实现

int dfs(int x, int fa, int mid) {
    int len = 0;
    multiset<int> s;
    for (int i = p[x]; i != -1; i = e[i].nxt) {
        int v = e[i].v, w = e[i].w, l;
        if (v == fa) {
            continue;
        }
        l = dfs(v, x, mid) + w;
        opt[x] += opt[v];
        if (l >= mid) {
            opt[x]++;
        } else {
            s.insert(l);
        }
    }
    while (!s.empty()) {
        int now = (*s.begin());
        s.erase(s.begin());
        multiset<int>::iterator it = s.lower_bound(mid - now);
        if (it != s.end()) {
            s.erase(it);
            opt[x]++;
        } else {
            len = now;
        }
    }
    return len;
}

至于菊花图的话可能会被卡？？？我没试过，如果担心的话可以特判一下，只需要一次排序然后lower_bound就OK了。

8.19更新

有同学不知道菊花图是什么



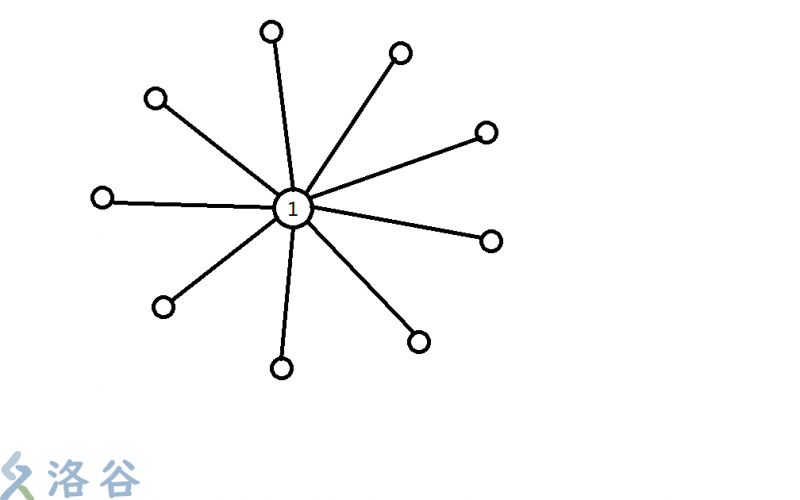
就是介个东西QWQ

菊花图通常会被卡，所以需要特判或者寻找更高效算法（ 一般是特判辣， 因为菊花图上的问题大部分比较简单的 ）

好像也没多少树上dp