数据关联分析 association analysis (Aprior算法，python代码）

1基本概念

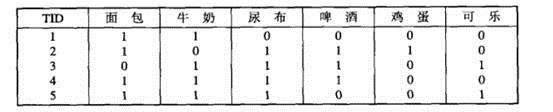
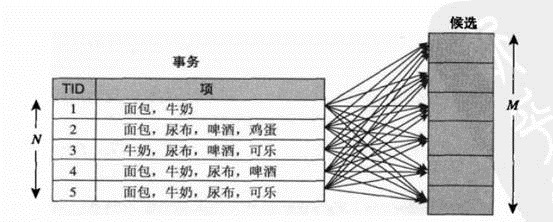
购物篮事务（market basket transaction),如下表，表中每一行对应一个事务，包含唯一标识TID,和购买的商品集合。本文介绍一种成为关联分析(association analysis)的方法，这种方法，可以从下表可以提取出，{尿布}—>牛奶.

两个关键问题：1大型数据计算量很大。2发现的某种模式可能是虚假，偶然发生的。

2问题定义

把数据可以转换为如下表的二元表示，非二元不在本文讨论范围

项集

项集的支持度计数：

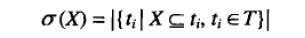
关联规则：

我们要发现，满足最小支持度与最小置信度的规则。

l 频繁项集(frequent itemset):发现满足最小支持度阈值的所有项集，这些项集成为频繁项集。

l 规则的产生：从上一步发现的频繁项集中提取所有高置信度的规则，这些规则成为强规则(strong rule)

频繁项集的产生

穷举法：

利用格结构（lattice structure）产生所有候选项集（candidate itemset）.

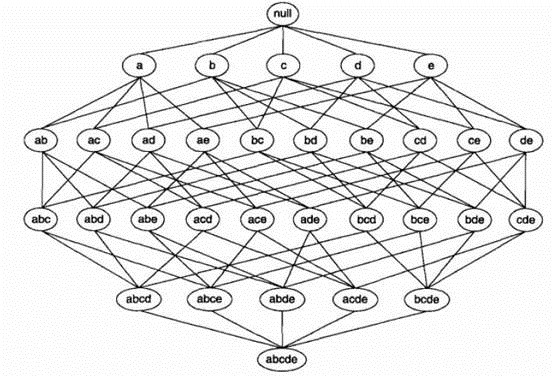
利用穷举法，计算每个候选项集的支持度计数。但是该方法计算量太大。

先验(apriori)原理：

如果一个项集是频繁的，则的所有子集一定是频繁的。若某项集是非频繁的，则其所有的超级也一定是非频繁的。

如下图，若{c,d,e}是频繁项集，则它的子集一定是频繁项集。

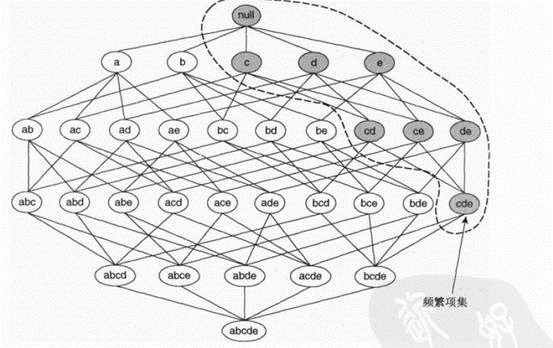
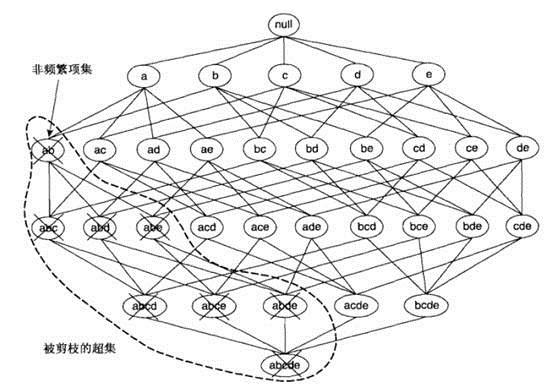
项集{a,b}是非频繁的，则其所有的超级也一定是非频繁的,如下图。

Aprior算法的频繁项集产生

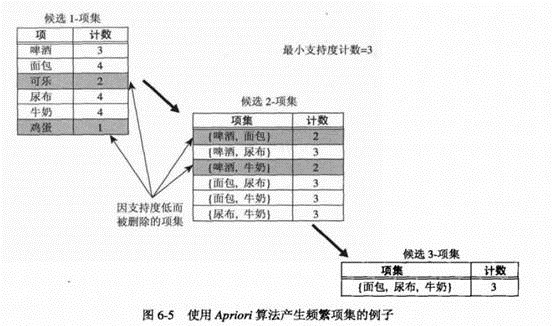
1. 确定每个1-项集的支持度计数，删除不满足最小支持度的1-项集。（步骤1,2）

2. 迭代：使用频繁(k-1)项集，产生新的候选k项集（步骤5）

3. 为了对候选k项集计算支持度计数，再次扫描数据(6-10)

4. 删去支持度小于最小支持度（minsup）的候选集

5. 当Fk=NULL,结束。

6. 候选集是所有频繁i项集的交际。i=1,2…

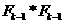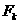方法：产生(频繁k-项集)。(step5)

函数aprior-gen的候选产生过程，合并一对频繁k-1项集，仅当他们前k-2个项都相同时，即

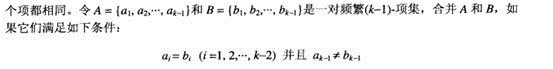
图例：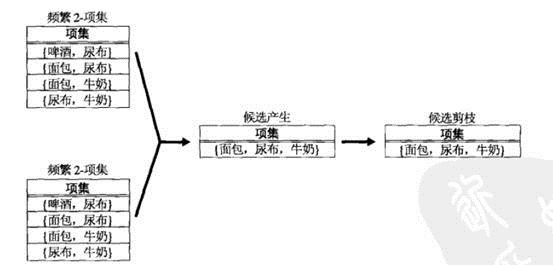

Python代码：

def aprioriGen(Lk,k):#create ck(k项集)
    retList=[]
    lenLk=len(Lk)
    for i in range(lenLk):
        for j in range(i+1,lenLk):
            L1=list(Lk[i])[:k-2];L2=list(Lk[j])[:k-2]
            L1.sort();L2.sort()#排序
            if L1==L2:#比较i,j前k-1个项若相同，和合并它俩
                retList.append(Lk[i] | Lk[j])#加入新的k项集 | stanf for union
    return retList

支持度计数：算法(6-12)代码

Python代码：

def scanD(D,ck,minSupport):#dataset,a list of candidate set,最小支持率
    ssCnt={}
    for tid in D:
        for can in ck:
            if can.issubset(tid):
                if not ssCnt.has_key(can):
                    ssCnt[can]=1
                else: ssCnt[can]+=1

    numItem=float(len(D))
    retList=[]
    supportData={}
    for key in ssCnt:
        support=ssCnt[key]/numItem
        if support>=minSupport:
            retList.insert(0,key)
            supportData[key]=support

    return retList,supportData#返回频繁k项集，相应支持度

频繁项集的产生：

def apriori(dataSet,minSupport=0.5):
    C1=createC1(dataSet)
    D=map(set,dataSet)
    L1,supportData=scanD(D,C1,minSupport)#利用k项集生成频繁k项集（即满足最小支持率的k项集）
    L=[L1]#L保存所有频繁项集

    k=2
    while(len(L[k-2])>0):#直到频繁k-1项集为空
        Ck=aprioriGen(L[k-2],k)#利用频繁k-1项集 生成k项集
        Lk,supK= scanD(D,Ck,minSupport)
        supportData.update(supK)#保存新的频繁项集与其支持度
        L.append(Lk)#保存频繁k项集
        k+=1
    return L,supportData#返回所有频繁项集，与其相应的支持率

规则产生(mining rules)

定理：

例如下：若bcd ->a是低置信度的，则它的子代都是低置信度的。利用此定理可以避免不必要的计算，减少运算复杂度。

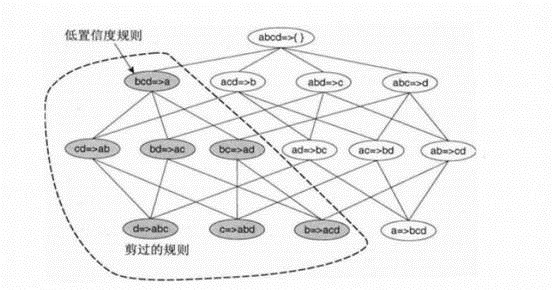
算法流程如下：

 

python代码：

def calcConf(freqSet,H,supportData,brl,minConf=0.7):
    prunedH=[]
    for conseq in H:#后件中的每个元素
        conf=supportData[freqSet]/supportData[freqSet-conseq]
        if conf>=minConf:
            print freqSet-conseq,'-->',conseq,'conf:',conf
            brl.append((freqSet-conseq,conseq,conf))#添加入规则集中
            prunedH.append(conseq)#添加入被修剪过的H中

    return prunedH

def rulesFromConseq(freqSet,H,supportData,brl,minConf=0.7):

    m=len(H[0])#H是一系列后件长度相同的规则，所以取H0的长度即可
    if (len(freqSet)>m+1):
        Hmp1=aprioriGen(H,m+1)
        Hmp1=calcConf(freqSet,Hmp1,supportData,brl,minConf)
        if (len(Hmp1)>1):
            rulesFromConseq(freqSet,Hmp1,supportData,brl,minConf)

def generateRules(L,supportData,minConf=0.7):
    import pdb
    pdb.set_trace()
    bigRuleList=[]#存储规则
    for i in range(1,len(L)):
        for freqSet in L[i]:
            H1=[frozenset([item]) for item in freqSet]
            if(i>1):
                rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
            else:
                calcConf(freqSet,H1,supportData,bigRuleList,minConf)
    return bigRuleList

 

 

 

整个prior算法的python代码

算法函数：

# -*- coding: utf-8 -*-
"""
Created on Wed Dec 04 22:25:57 2013

@author: Administrator
"""

def loadDataSet():
    return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]

def createC1(dataSet):#产生单个item的集合
    C1=[]
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])

    C1.sort()

    return map(frozenset,C1)#给C1.list每个元素执行函数

def scanD(D,ck,minSupport):#dataset,a list of candidate set,最小支持率
    ssCnt={}
    for tid in D:
        for can in ck:
            if can.issubset(tid):
                if not ssCnt.has_key(can):
                    ssCnt[can]=1
                else: ssCnt[can]+=1

    numItem=float(len(D))
    retList=[]
    supportData={}
    for key in ssCnt:
        support=ssCnt[key]/numItem
        if support>=minSupport:
            retList.insert(0,key)
            supportData[key]=support

    return retList,supportData#返回频繁k项集，相应支持度

def aprioriGen(Lk,k):#create ck(k项集)
    retList=[]
    lenLk=len(Lk)
    for i in range(lenLk):
        for j in range(i+1,lenLk):
            L1=list(Lk[i])[:k-2];L2=list(Lk[j])[:k-2]
            L1.sort();L2.sort()#排序
            if L1==L2:#比较i,j前k-1个项若相同，和合并它俩
                retList.append(Lk[i] | Lk[j])#加入新的k项集 | stanf for union
    return retList

def apriori(dataSet,minSupport=0.5):
    C1=createC1(dataSet)
    D=map(set,dataSet)
    L1,supportData=scanD(D,C1,minSupport)#利用k项集生成频繁k项集（即满足最小支持率的k项集）
    L=[L1]#L保存所有频繁项集

    k=2
    while(len(L[k-2])>0):#直到频繁k-1项集为空
        Ck=aprioriGen(L[k-2],k)#利用频繁k-1项集 生成k项集
        Lk,supK= scanD(D,Ck,minSupport)
        supportData.update(supK)#保存新的频繁项集与其支持度
        L.append(Lk)#保存频繁k项集
        k+=1
    return L,supportData#返回所有频繁项集，与其相应的支持率

def calcConf(freqSet,H,supportData,brl,minConf=0.7):
    prunedH=[]
    for conseq in H:#后件中的每个元素
        conf=supportData[freqSet]/supportData[freqSet-conseq]
        if conf>=minConf:
            print freqSet-conseq,'-->',conseq,'conf:',conf
            brl.append((freqSet-conseq,conseq,conf))#添加入规则集中
            prunedH.append(conseq)#添加入被修剪过的H中

    return prunedH

def rulesFromConseq(freqSet,H,supportData,brl,minConf=0.7):

    m=len(H[0])#H是一系列后件长度相同的规则，所以取H0的长度即可
    if (len(freqSet)>m+1):
        Hmp1=aprioriGen(H,m+1)
        Hmp1=calcConf(freqSet,Hmp1,supportData,brl,minConf)
        if (len(Hmp1)>1):
            rulesFromConseq(freqSet,Hmp1,supportData,brl,minConf)

def generateRules(L,supportData,minConf=0.7):

    bigRuleList=[]#存储规则
    for i in range(1,len(L)):
        for freqSet in L[i]:
            H1=[frozenset([item]) for item in freqSet]
            if(i>1):
                rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
            else:
                calcConf(freqSet,H1,supportData,bigRuleList,minConf)
    return bigRuleList

 

测试代码：

import apriori
dataSet=apriori.loadDataSet()

C1=apriori.createC1(dataSet)

D=map(set,dataSet)
L1,suppData0=apriori.scanD(D,C1,0.5)

L,suppData=apriori.apriori(dataSet)

print L
rules=apriori.generateRules(L,suppData,minConf=0.5)

 

 

参数文献：

1数据挖掘导论

2machine learning in action